No CrossRef data available.
Article contents
ON THE LND CONJECTURE
Published online by Cambridge University Press: 03 July 2023
Abstract
Let k be a field of characteristic zero and 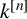 $k^{[n]}$ the polynomial algebra in n variables over k. The LND conjecture concerning the images of locally nilpotent derivations arose from the Jacobian conjecture. We give a positive answer to the LND conjecture in several cases. More precisely, we prove that the images of rank-one locally nilpotent derivations of
$k^{[n]}$ the polynomial algebra in n variables over k. The LND conjecture concerning the images of locally nilpotent derivations arose from the Jacobian conjecture. We give a positive answer to the LND conjecture in several cases. More precisely, we prove that the images of rank-one locally nilpotent derivations of 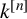 $k^{[n]}$ acting on principal ideals are MZ-subspaces for any
$k^{[n]}$ acting on principal ideals are MZ-subspaces for any 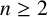 $n\geq 2$, and that the images of a large class of locally nilpotent derivations of
$n\geq 2$, and that the images of a large class of locally nilpotent derivations of 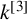 $k^{[3]}$ (including all rank-two and homogeneous rank-three locally nilpotent derivations) acting on principal ideals are MZ-subspaces.
$k^{[3]}$ (including all rank-two and homogeneous rank-three locally nilpotent derivations) acting on principal ideals are MZ-subspaces.
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 108 , Issue 3 , December 2023 , pp. 412 - 421
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
This work was supported by the EDJPC (JJKH20220962KJ), NSFJP (20210101469JC) and NSFC (12171194).



