Hostname: page-component-6bf8c574d5-t27h7 Total loading time: 0 Render date: 2025-02-27T01:03:15.053Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE NUMBER OF NEARLY SELF-CONJUGATE PARTITIONS

Part of: Combinatorics Additive number theory; partitions

Published online by Cambridge University Press:  11 November 2022

BERNARD L. S. LIN Open the ORCID record for BERNARD L. S. LIN [Opens in a new window]  and
SITONG SUN Open the ORCID record for SITONG SUN [Opens in a new window]
BERNARD L. S. LIN*
Affiliation:
School of Science, Jimei University, Xiamen 361021, PR China
SITONG SUN
Affiliation:
School of Science, Jimei University, Xiamen 361021, PR China e-mail: sunstong@163.com
*
e-mail: linlsjmu@163.com
Get access Rights & Permissions [Opens in a new window]

Abstract

A partition 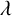$\lambda $ of n is said to be nearly self-conjugate if the Ferrers graph of 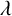$\lambda $ and its transpose have exactly 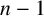$n-1$ cells in common. The generating function of the number of such partitions was first conjectured by Campbell and recently confirmed by Campbell and Chern (‘Nearly self-conjugate integer partitions’, submitted for publication). We present a simple and direct analytic proof and a combinatorial proof of an equivalent statement.

Keywords

nearly self-conjugate integer partitionFrobenius symbolgenerating function

MSC classification

Primary: 11P81: Elementary theory of partitions
Secondary: 05A17: Partitions of integers
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 108 , Issue 1 , August 2023 , pp. 114 - 119
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by the National Natural Science Foundation of China (No. 11871246).

References

Andrews, G. E., The Theory of Partitions (Addison-Wesley, Reading, MA, 1976).Google Scholar
Andrews, G. E. and Ballantine, C., ‘Almost partition identities’, Proc. Natl. Acad. Sci. USA 116 (2019), 5428–5436.CrossRefGoogle ScholarPubMed
Andrews, G. E. and Eriksson, K., Integer Partitions (Cambridge University Press, Cambridge, 2004).CrossRefGoogle Scholar
Campbell, J. M., ‘Sequence A246581’, On-Line Encyclopedia of Integer Sequences, Sloane, N. J. A. (ed.), http://oeis.org.Google Scholar
Sylvester, J. J., ‘A constructive theory of partitions in three acts, an interact, and an exodion’, Amer. J. Math. 5 (1882), 251–330.CrossRefGoogle Scholar