ON THE PARITY OF THE GENERALISED FROBENIUS PARTITION FUNCTIONS 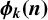$\boldsymbol {\phi _k(n)}$

Abstract

Andrews [Generalized Frobenius Partitions, Memoirs of the American Mathematical Society, 301 (American Mathematical Society, Providence, RI, 1984)] defined two families of functions, 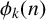$\phi _k(n)$ and 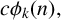$c\phi _k(n),$ enumerating two types of combinatorial objects which he called generalised Frobenius partitions. Andrews proved a number of Ramanujan-like congruences satisfied by specific functions within these two families. Numerous other authors proved similar results for these functions, often with a view towards a specific choice of the parameter 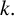$k.$ Our goal is to identify an infinite family of values of k such that 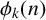$\phi _k(n)$ is even for all n in a specific arithmetic progression; in particular, we prove that, for all positive integers 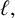$\ell ,$ all primes 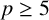$p\geq 5$ and all values 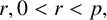$r, 0 < r < p,$ such that 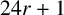$24r+1$ is a quadratic nonresidue modulo 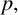$p,$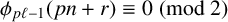

$$ \begin{align*} \phi_{p\ell-1}(pn+r) \equiv 0 \pmod{2} \end{align*} $$

for all 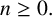$n\geq 0.$ Our proof of this result is truly elementary, relying on a lemma from Andrews’ memoir, classical q-series results and elementary generating function manipulations. Such a result, which holds for infinitely many values of 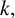$k,$ is rare in the study of arithmetic properties satisfied by generalised Frobenius partitions, primarily because of the unwieldy nature of the generating functions in question.