PROOF OF A CONJECTURE OF BANERJEE AND DASTIDAR ON ODD CRANK

Abstract

Recently, when studying intricate connections between Ramanujan’s theta functions and a class of partition functions, Banerjee and Dastidar [‘Ramanujan’s theta functions and parity of parts and cranks of partitions’, Ann. Comb., to appear] studied some arithmetic properties for 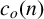$c_o(n)$, the number of partitions of n with odd crank. They conjectured a congruence modulo 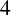$4$ satisfied by 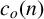$c_o(n)$. We confirm the conjecture and evaluate 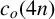$c_o(4n)$ modulo 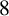$8$ by dissecting some q-series into even powers. Moreover, we give a conjecture on the density of divisibility of odd cranks modulo 4, 8 and 16.

1 Introduction

A partition $\lambda$ of a nonnegative integer n is a finite weakly decreasing sequence of positive integers $\lambda _1\geq \lambda _2\geq \cdots \geq \lambda _r$ such that $\sum _{i=1}^r\lambda _i=n$ . The $\lambda _i$ for $1\leq i\leq r$ are called the parts of the partition $\lambda $ . Let $p(n)$ denote the number of partitions of n. In 1919, Ramanujan [8] discovered three remarkable congruences enjoyed by $p(n)$ , namely,

(1.1) $$ \begin{align} p(5n+4) &\equiv0 \pmod{5}, \end{align} $$

(1.2) $$ \begin{align} p(7n+5) &\equiv0 \pmod{7}, \end{align} $$

(1.3) $$ \begin{align} p(11n+6) &\equiv0 \pmod{11}. \end{align} $$

In 1944, Dyson [7] introduced the notion of the rank, and further conjectured that this partition statistic could provide a combinatorial interpretation for (1.1) and (1.2). Dyson’s conjecture was later confirmed by Atkin and Swinnerton-Dyer [4] in 1954. Unfortunately, this partition statistic cannot interpret (1.3) combinatorially. Therefore, Dyson further conjectured that there exists another statistic, which he named the ‘crank’, providing a combinatorial interpretation of (1.3). This partition statistic was discovered by Andrews and Garvan [3] in 1988. For a partition $\lambda $ , let $l(\lambda )$ denote the largest part of $\lambda $ , let $\omega (\lambda )$ and $\mu (\lambda )$ denote the number of ones in $\lambda $ and the number of parts of $\lambda $ that are larger than $\omega (\lambda )$ , respectively. The crank is defined by

$$ \begin{align*} \textrm{crank}(\lambda)= \begin{cases} l(\lambda) \quad &\textrm{if }\omega(\lambda)=0,\\ \omega(\lambda)-\mu(\lambda) \quad &\textrm{if }\omega(\lambda)>0. \end{cases} \end{align*} $$

Let $c_o(n)$ denote the number of partitions of n with odd crank. The generating function of $c_o(n)$ is given by

$$ \begin{align*} \sum_{n=0}^\infty c_o(n)q^n=\dfrac{1}{2} {\bigg(\dfrac{1}{(q;q)_\infty}-\dfrac{(q;q)_\infty^3}{(q^2;q^2)_\infty^2}\bigg)}. \end{align*} $$

Throughout the rest of this paper, we always assume that q is a complex number such that $|q|<1$ and adopt the following customary notation:

$$ \begin{align*} (a;q)_\infty &:=\prod_{k=0}^\infty(1-aq^k),\\ (a_1,a_2,\ldots,a_m;q)_\infty &:=(a_1;q)_\infty(a_2;q)_\infty\cdots(a_m;q)_\infty. \end{align*} $$

Recently, Banerjee and Dastidar [5] considered some arithmetic properties of $c_o(n)$ . By means of q-series manipulations, Banerjee and Dastidar [5, (1.10)] proved that for any $n\geq 0$ ,

$$ \begin{align*} c_o(5n+4)\equiv0 \pmod{10}. \end{align*} $$

Based on computer experiments, they conjectured a congruence modulo $4$ satisfied by $c_o(n)$ .

Conjecture 1.1. We have $c_o(2n)\equiv 0 \pmod {4}$ for any $n\geq 0$ .

Banerjee and Dastidar [5] verified that Conjecture 1.1 holds for any $1\leq n\leq 2000$ . By using some q-series techniques, we not only confirm the above congruence modulo  $4$ , but also establish another congruence modulo $8$ .

Theorem 1.2. For any $n\geq 0$ ,

(1.4) $$ \begin{align} c_o(2n) &\equiv0 \pmod{4}, \end{align} $$

(1.5) $$ \begin{align} c_o(4n) &\equiv0 \pmod{8}. \end{align} $$

2 Proof of Theorem 1.2

To prove (1.4) and (1.5), we need the following three auxiliary identities.

Lemma 2.1 [2, Lemma 4.1]

We have

(2.1) $$ \begin{align} \dfrac{1}{(q;q)_\infty}=\dfrac{1}{(q^2;q^2)_\infty^2} ((-q^6,-q^{10},q^{16};q^{16})_\infty+q(-q^2,-q^{14},q^{16};q^{16})_\infty). \end{align} $$

Lemma 2.2 (Jacobi’s identity [6, Theorem 1.3.9])

(2.2) $$ \begin{align} (q;q)_\infty^3=\sum_{n=0}^\infty(-1)^n(2n+1)q^{n(n+1)/2}. \end{align} $$

Lemma 2.3 (Jacobi’s triple product identity [1, Lemma 1.2.2])

(2.3) $$ \begin{align} \sum_{n=-\infty}^\infty a^{n(n+1)/2}b^{n(n-1)/2}=(-a,-b,ab;ab)_\infty,\quad|ab|<1. \end{align} $$

Now we are in a position to prove Theorem 1.2.

Proof of Theorem 1.2

Define the sequence $\{A(n)\}_{n\geq 0}$ by

(2.4) $$ \begin{align} \sum_{n=0}^\infty A(n)q^n=\dfrac{1}{(q;q)_\infty}-\dfrac{(q;q)_\infty^3}{(q^2;q^2)_\infty^2}. \end{align} $$

Therefore, (1.4) and (1.5) are equivalent respectively to

(2.5) $$ \begin{align} A(2n) &\equiv0 \pmod{8}, \end{align} $$

and

(2.6) $$ \begin{align} A(4n) &\equiv0 \pmod{16}. \end{align} $$

However, from (2.2),

$$ \begin{align*} (q;q)_\infty^3 &=\sum_{n=0}^\infty(-1)^n(2n+1)q^{n(n+1)/2}\\ &=\sum_{n=0}^\infty(-1)^{8n}(16n+1)q^{4n(8n+1)}+\sum_{n=0}^\infty(-1)^{8n+1}(16n+3)q^{(4n+1)(8n+1)}\\ &\quad+\sum_{n=0}^\infty(-1)^{8n+2}(16n+5)q^{(4n+1)(8n+3)}+\sum_{n=0}^\infty(-1)^{8n+3}(16n+7)q^{(4n+2)(8n+3)}\\ &\quad+\sum_{n=0}^\infty(-1)^{8n+4}(16n+9)q^{(4n+2)(8n+5)}+\sum_{n=0}^\infty(-1)^{8n+5}(16n+11)q^{(4n+3)(8n+5)}\\ &\quad+\sum_{n=0}^\infty(-1)^{8n+6}(16n+13)q^{(4n+3)(8n+7)}+\sum_{n=0}^\infty(-1)^{8n+7}(16n+15)q^{(4n+4)(8n+7)},\end{align*} $$

from which we further obtain that

(2.7) $$ \begin{align} (q;q)_\infty^3 &\equiv\sum_{n=0}^\infty q^{4n(8n+1)}-3\sum_{n=0}^\infty q^{(4n+1)(8n+1)}\notag\\ &\quad+5\sum_{n=0}^\infty q^{(4n+1)(8n+3)}-7\sum_{n=0}^\infty q^{(4n+2)(8n+3)} \nonumber \\&\quad-7\sum_{n=0}^\infty q^{(4n+2)(8n+5)}+5\sum_{n=0}^\infty q^{(4n+3)(8n+5)}\notag\\ &\quad-3\sum_{n=0}^\infty q^{(4n+3)(8n+7)}+\sum_{n=0}^\infty q^{(4n+4)(8n+7)} \pmod{16}. \end{align} $$

Replacing n by $-n-1$ in the last four infinite sums in (2.7),

(2.8) $$ \begin{align} \sum_{n=0}^\infty q^{(4n+2)(8n+5)} &=\sum_{n=-\infty}^{-1}q^{(4n+2)(8n+3)}, \end{align} $$

(2.9) $$ \begin{align} \sum_{n=0}^\infty q^{(4n+3)(8n+5)} &=\sum_{n=-\infty}^{-1}q^{(4n+1)(8n+3)}, \end{align} $$

(2.10) $$ \begin{align} \sum_{n=0}^\infty q^{(4n+3)(8n+7)} &=\sum_{n=-\infty}^{-1}q^{(4n+1)(8n+1)}, \end{align} $$

(2.11) $$ \begin{align} \kern-15pt\sum_{n=0}^\infty q^{(4n+4)(8n+7)} &=\sum_{n=-\infty}^{-1}q^{4n(8n+1)}. \end{align} $$

Substituting (2.8)–(2.11) into (2.9),

$$ \begin{align*} (q;q)_\infty^3 &\equiv\sum_{n=-\infty}^\infty q^{4n(8n+1)}-3\sum_{n=-\infty}^\infty q^{(4n+1)(8n+1)}\notag\\ &\quad+5\sum_{n=-\infty}^\infty q^{(4n+1)(8n+3)}-7\sum_{n=-\infty}^\infty q^{(4n+2)(8n+3)} \pmod{16}. \end{align*} $$

Thanks to (2.3),

(2.12) $$ \begin{align} (q;q)_\infty^3 &\equiv(-q^{28},-q^{36},q^{64};q^{64})_\infty-3q(-q^{20},-q^{44},q^{64};q^{64})_\infty\notag\\[4pt] &\quad+5q^3(-q^{12},-q^{52},q^{64};q^{64})_\infty-7q^6(-q^4,-q^{60},q^{64};q^{64})_\infty \pmod{16}. \end{align} $$

Substituting (2.1) and (2.12) into (2.4) yields

(2.13) $$ \begin{align} \sum_{n=0}^\infty A(n)q^n &\equiv\dfrac{1}{(q^2;q^2)_\infty^2} ((-q^6,-q^{10},q^{16};q^{16})_\infty+q(-q^2,-q^{14},q^{16};q^{16})_\infty)\notag\\ &\quad-\dfrac{1}{(q^2;q^2)_\infty^2}((-q^{28},-q^{36},q^{64};q^{64})_\infty-3q(-q^{20},-q^{44},q^{64};q^{64})_\infty\notag\\[4pt] &\qquad+5q^3(-q^{12},-q^{52},q^{64};q^{64})_\infty-7q^6(-q^4,-q^{60},q^{64};q^{64})_\infty) \pmod{16}.\end{align} $$

Taking all terms of the form $q^{2n}$ in (2.13), after simplification,

(2.14) $$ \begin{align} \sum_{n=0}^\infty A(2n)q^n &\equiv\dfrac{1}{(q;q)_\infty^2} ((-q^3,-q^5,q^8;q^8)_\infty-(-q^{14},-q^{18},q^{32};q^{32})_\infty\notag\\ &\quad+7q^3(-q^2,-q^{30},q^{32};q^{32})_\infty) \pmod{16}. \end{align} $$

According to (2.3),

(2.15) $$ \begin{align} (-q^3,-q^5,q^8;q^8)_\infty &=\sum_{n=-\infty}^\infty q^{4n^2+n}\notag\\ &=\sum_{n=-\infty}^\infty q^{4(2n)^2+2n}+\sum_{n=-\infty}^\infty q^{4(2n-1)^2+(2n-1)}\notag\\ &=\sum_{n=-\infty}^\infty q^{16n^2+2n}+\sum_{n=-\infty}^\infty q^{16n^2-14n+3}\notag\\ &=(-q^{14},-q^{18},q^{32};q^{32})_\infty+q^3(-q^2,-q^{30},q^{32};q^{32})_\infty, \end{align} $$

where we have used (2.3) in the last step. Combining (2.14) and (2.15) gives

(2.16) $$ \begin{align} \sum_{n=0}^\infty A(2n)q^n\equiv 8q^3\dfrac{(-q^2,-q^{30},q^{32};q^{32})_\infty}{(q;q)_\infty^2} \pmod{16}. \end{align} $$

The congruence (2.5) follows immediately from (2.16).

Moreover, from the congruence $(q;q)_\infty ^2\equiv (q^2;q^2)_\infty \pmod {2}$ ,

(2.17) $$ \begin{align} \sum_{n=0}^\infty A(2n)q^n\equiv8q^3\dfrac{(-q^2,-q^{30},q^{32};q^{32})_\infty}{(q^2;q^2)_\infty} \pmod{16}. \end{align} $$

The congruence (2.6) follows immediately from (2.17).

This completes the proof of Theorem 1.2.

3 Concluding remarks

We conclude this paper with two remarks.

First, the numerical evidence suggests the following conjecture.

Conjecture 3.1. We have

$$ \begin{align*} \lim_{n\rightarrow\infty}\dfrac{\#\{m|\:c_o(2m+1)\equiv0 \pmod{4},\;\;1\leq m\leq n\}}{n} &=\dfrac{1}{2},\\ \lim_{n\rightarrow\infty}\dfrac{\#\{m|\:c_o(2m)\equiv0 \pmod{8},\;\;1\leq m\leq n\}}{n} &=\dfrac{1}{4},\\ \lim_{n\rightarrow\infty}\dfrac{\#\{m|\:c_o(4m+2)\equiv0 \pmod{8},\;\;1\leq m\leq n\}}{n} &=\dfrac{1}{2},\\ \lim_{n\rightarrow\infty}\dfrac{\#\{m|\:c_o(4m)\equiv0 \pmod{16},\;\;1\leq m\leq n\}}{n} &=\dfrac{1}{2}. \end{align*} $$

Second, it would be interesting find a combinatorial proof of (1.4) and (1.5).