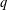 $q$-ANALOGUE OF A HYPERGEOMETRIC CONGRUENCE
$q$-ANALOGUE OF A HYPERGEOMETRIC CONGRUENCEPublished online by Cambridge University Press: 18 July 2019
We give a 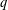 $q$-analogue of the following congruence: for any odd prime
$q$-analogue of the following congruence: for any odd prime 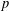 $p$, which was originally conjectured by Long and later proved by Swisher. This confirms a conjecture of the second author [‘A
$p$, which was originally conjectured by Long and later proved by Swisher. This confirms a conjecture of the second author [‘A 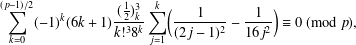 $$\begin{eqnarray}\mathop{\sum }_{k=0}^{(p-1)/2}(-1)^{k}(6k+1)\frac{(\frac{1}{2})_{k}^{3}}{k!^{3}8^{k}}\mathop{\sum }_{j=1}^{k}\biggl(\frac{1}{(2j-1)^{2}}-\frac{1}{16j^{2}}\biggr)\equiv 0\;(\text{mod}\;p),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{k=0}^{(p-1)/2}(-1)^{k}(6k+1)\frac{(\frac{1}{2})_{k}^{3}}{k!^{3}8^{k}}\mathop{\sum }_{j=1}^{k}\biggl(\frac{1}{(2j-1)^{2}}-\frac{1}{16j^{2}}\biggr)\equiv 0\;(\text{mod}\;p),\end{eqnarray}$$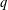 $q$-analogue of the (L.2) supercongruence of Van Hamme’, J. Math. Anal. Appl. 466 (2018), 749–761].
$q$-analogue of the (L.2) supercongruence of Van Hamme’, J. Math. Anal. Appl. 466 (2018), 749–761].
The second author was partially supported by the National Natural Science Foundation of China (grant 11771175).