Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T14:48:41.118Z Has data issue: false hasContentIssue false
  • English
  • Français

THE SLOT LENGTH OF A FAMILY OF MATRICES

Part of: Basic linear algebra

Published online by Cambridge University Press:  05 October 2020

W. E. LONGSTAFF Open the ORCID record for W. E. LONGSTAFF [Opens in a new window]
W. E. LONGSTAFF*
Affiliation:
11 Tussock Crescent, Elanora, Queensland4221, Australia
*
e-mail: bill.longstaff@alumni.utoronto.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce the notion of the slot length of a family of matrices over an arbitrary field 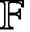${\mathbb {F}}$ . Using this definition it is shown that, if 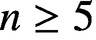$n\ge 5$ and A and B are 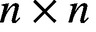$n\times n$ complex matrices with A unicellular and the pair 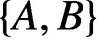$\{A,B\}$ irreducible, the slot length s of 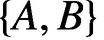$\{A,B\}$ satisfies 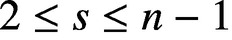$2\le s\le n-1$ , where both inequalities are sharp, for every n. It is conjectured that the slot length of any irreducible pair of 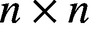$n\times n$ matrices, where 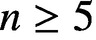$n\ge 5$ , is at most 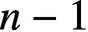$n-1$ . The slot length of a family of rank-one complex matrices can be equal to n.

Keywords

irreduciblelinear span

MSC classification

Primary: 15A30: Algebraic systems of matrices
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 2 , April 2021 , pp. 260 - 270
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Guterman, A. E., Laffey, T., Markova, O. V. and Smigoc, H., ‘A resolution of Paz’s conjecture in the presence of a nonderogatory matrix’, Linear Algebra Appl. 543 (2018), 234–250.CrossRefGoogle Scholar
Lomonosov, V. and Rosenthal, P., ‘The simplest proof of Burnside’s theorem on matrix algebras’, Linear Algebra Appl. 383 (2004), 45–47.CrossRefGoogle Scholar
Longstaff, W. E., ‘Burnside’s theorem: irreducible pairs of transformations’, Linear Algebra Appl. 382 (2004), 247–269.CrossRefGoogle Scholar
Longstaff, W. E., ‘Irreducible families of complex matrices containing a rank one matrix’, Bull. Aust. Math. Soc. 102(2) (2020), 226–236.CrossRefGoogle Scholar
Longstaff, W. E., Niemeyer, A. C. and Panaia, O., ‘On the lengths of pairs of complex matrices of size at most five’, Bull. Aust. Math. Soc. 73 (2006), 461–472.CrossRefGoogle Scholar
Longstaff, W. E. and Rosenthal, P., ‘On the lengths of irreducible pairs of complex matrices’, Proc. Amer. Math. Soc. 139(11) (2011), 3769–3777.CrossRefGoogle Scholar
Markova, O.V., ‘The length function and matrix algebras’, Fundam. Prikl. Mat. 17(6) (2012), 65–173. English transl. J. Math. Sci. (N. Y.) 193(5) (2013), 687–768.Google Scholar
Paz, A., ‘An application of the Cayley-Hamilton theorem to matrix polynomials in several variables’, Linear Multilinear Algebra 15 (1984), 161–170.CrossRefGoogle Scholar
Shitov, Y., ‘An improved bound for the lengths of matrix algebras’ (English summary), Algebra Number Theory 13(6) (2019), 1501–1507.CrossRefGoogle Scholar