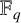Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Asgarli, Shamil
Ghioca, Dragos
and
Yip, Chi Hoi
2023.
Plane curves giving rise to blocking sets over finite fields.
Designs, Codes and Cryptography,
Vol. 91,
Issue. 11,
p.
3643.
Asgarli, Shamil
Ghioca, Dragos
and
Yip, Chi Hoi
2023.
Existence of pencils with nonblocking hypersurfaces.
Finite Fields and Their Applications,
Vol. 92,
Issue. ,
p.
102283.
Asgarli, Shamil
Ghioca, Dragos
and
Reichstein, Zinovy
2023.
Linear families of smooth hypersurfaces over finitely generated fields.
Finite Fields and Their Applications,
Vol. 87,
Issue. ,
p.
102169.
ASGARLI, SHAMIL
and
GHIOCA, DRAGOS
2024.
TANGENT-FILLING PLANE CURVES OVER FINITE FIELDS.
Bulletin of the Australian Mathematical Society,
Vol. 109,
Issue. 2,
p.
301.