No CrossRef data available.
Article contents
TWO SUPERCONGRUENCES RELATED TO MULTIPLE HARMONIC SUMS
Published online by Cambridge University Press: 28 January 2021
Abstract
Let p be a prime and let x be a p-adic integer. We prove two supercongruences for truncated series of the form 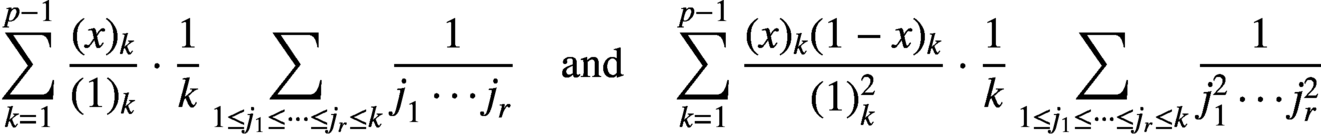
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2021 Australian Mathematical Publishing Association Inc.



