Hostname: page-component-6bf8c574d5-7jkgd Total loading time: 0 Render date: 2025-02-26T14:58:34.731Z Has data issue: false hasContentIssue false
  • English
  • Français

THE ABSOLUTE 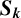$\boldsymbol {S_k}$-MEASURE OF TOTALLY POSITIVE ALGEBRAIC INTEGERS

Part of: Algebraic number theory: global fields Computational number theory Polynomials and matrices

Published online by Cambridge University Press:  11 August 2022

CONG WANG Open the ORCID record for CONG WANG [Opens in a new window] ,
XIAOJUAN PANG Open the ORCID record for XIAOJUAN PANG [Opens in a new window]  and
QIANG WU Open the ORCID record for QIANG WU [Opens in a new window]
CONG WANG
Affiliation:
Department of Mathematics, Southwest University of China, 2 Tiansheng Road, Beibei 400715, Chongqing, China e-mail: wangcong.swu@foxmail.com
XIAOJUAN PANG
Affiliation:
Department of Mathematics, Southwest University of China, 2 Tiansheng Road, Beibei 400715, Chongqing, China e-mail: xiaojuan.pang@foxmail.com
QIANG WU*
Affiliation:
Department of Mathematics, Southwest University of China, 2 Tiansheng Road, Beibei 400715, Chongqing, China
*
e-mail: qiangwu@swu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 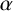$\alpha $ be a totally positive algebraic integer of degree d, with conjugates 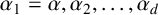$\alpha _1=\alpha , \alpha _2, \ldots , \alpha _d$ . The absolute 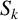$S_k$ -measure of 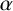$\alpha $ is defined by 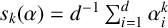$s_k(\alpha )= d^{-1} \sum _{i=1}^{d}\alpha _i^k$ . We compute the lower bounds 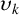$\upsilon _k$ of 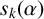$s_k(\alpha )$ for each integer in the range 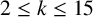$2\leq k \leq 15$ and give a conjecture on the results for integers $k>15$ . Then we derive the lower bounds of 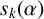$s_k(\alpha )$ for all real numbers 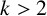$k>2$ . Our computation is based on an improvement in the application of the LLL algorithm and analysis of the polynomials in the explicit auxiliary functions.

Keywords

Sk-measuretotally positive algebraic integerexplicit auxiliary functionLLL algorithmsemi-infinite linear programming

MSC classification

Primary: 11R06: PV-numbers and generalizations; other special algebraic numbers; Mahler measure
Secondary: 11C08: Polynomials 11Y40: Algebraic number theory computations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 107 , Issue 2 , April 2023 , pp. 239 - 249
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported in part by the National Natural Science Foundation of China (grant no. 12071375).

References

Aguirre, J. and Peral, J. C., ‘The trace problem for totally positive algebraic integers’, in: Number Theory and Polynomials, London Mathematical Society Lecture Note Series, 352 (eds. McKee, J. and Smyth, C. J.) (Cambridge University Press, Cambridge, 2008), 1–19. With an appendix by Jean-Pierre Serre.Google Scholar
Amoroso, F., ‘ $f$ -transfinite diameter and number theoretic applications’, Ann. Inst. Fourier (Grenoble) 43 (1993), 1179–1198.CrossRefGoogle Scholar
Borwein, P., Computational Excursions in Analysis and Number Theory, CMS Books in Mathematics, 10 (Springer-Verlag, New York, 2002).CrossRefGoogle Scholar
Flammang, V., ‘Trace of totally positive algebraic integers and integer transfinite diameter’, Math. Comp. 78 (2009), 1119–1125.CrossRefGoogle Scholar
Flammang, V., ‘Comparison of measures of totally positive polynomials’, Bull. Aust. Math. Soc. 89 (2014), 265–270.CrossRefGoogle Scholar
Flammang, V., ‘On the absolute length of polynomials having all zeros in a sector’, J. Number Theory 143 (2014), 385–401.CrossRefGoogle Scholar
Flammang, V., ‘The Mahler measure and its areal analog for totally positive algebraic integers’, J. Number Theory 151 (2015), 211–222.CrossRefGoogle Scholar
Flammang, V., ‘Une nouvelle minoration pour la trace absolue des entiers algébriques totalement positifs’, Preprint, 2016, arXiv:1907.09407.Google Scholar
Flammang, V., ‘An analog to the Schur–Siegel–Smyth trace problem’, Math. Comp. 325 (2020), 2387–2398.CrossRefGoogle Scholar
Lenstra, A. K., Lenstra, H. W. and Lovász, L., ‘Factoring polynomials with rational coefficients’, Math. Ann. 261 (1982), 515–534.CrossRefGoogle Scholar
Liang, Y. and Wu, Q., ‘The trace problem for totally positive algebraic integers’, J. Aust. Math. Soc. 90 (2011), 341–354.CrossRefGoogle Scholar
McAuley, M. J., Topics in J-Fields and a Diameter Problem, MSc thesis, University of Adelaide, 1981.Google Scholar
Mossinghoff, M. J., Rhin, G. and Wu, Q., ‘Minimal Mahler measures’, Exp. Math. 17 (2008), 451–458.CrossRefGoogle Scholar
Mu, Q. and Wu, Q., ‘The measure of totally positive algebraic integers’, J. Number Theory 133 (2013), 12–19.CrossRefGoogle Scholar
Rhin, G. and Wu, Q., ‘On the smallest value of the maximal modulus of an algebraic integer’, Math. Comp. 76 (2007), 1025–1038.CrossRefGoogle Scholar
Robinson, M., ‘Algebraic equations with span less than 4’, Math. Comp. 18 (1964), 547–559.CrossRefGoogle Scholar
Schur, I., ‘Über die Verteilung der Wurzeln bei gewissen algebraischen Gleichungen mit ganzzahligen Koeffizienten’, Math. Z. 1 (1918), 377–402.CrossRefGoogle Scholar
Siegel, C. L., ‘The trace of totally positive and real algebraic integers’, Ann. of Math. (2) 46 (1945), 302–312.CrossRefGoogle Scholar
Smith, A., ‘Algebraic integers with conjugates in a prescribed distribution’, Preprint, 2021, arXiv:2111.12660.Google Scholar
Smyth, C. J., ‘Totally positive algebraic integers of small trace’, Ann. Inst. Fourier (Grenoble) 34 (1984), 1–28.CrossRefGoogle Scholar
Smyth, C. J., ‘The mean values of totally real algebraic integers’, Math. Comp. 42 (1984), 663–681.CrossRefGoogle Scholar
Wang, C., Wu, J. and Wu, Q., ‘Totally positive algebraic integers with small trace’, Math. Comp. 90 (2021), 2317–2332.CrossRefGoogle Scholar
Wu, Q., ‘On the linear independence measure of logarithms of rational numbers’, Math. Comp. 72 (2003), 901–911.CrossRefGoogle Scholar
Wu, Q., ‘The smallest Perron numbers’, Math. Comp. 79 (2010), 2387–2394.CrossRefGoogle Scholar