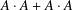Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Li, Jianghua
and
Li, Qiao
2020.
On the distribution of Low Hamming Weight products.
Journal of Inequalities and Applications,
Vol. 2020,
Issue. 1,
Agrawal, Komal
and
Pollack, Paul
2021.
Finite sets containing near-primitive roots.
Journal of Number Theory,
Vol. 225,
Issue. ,
p.
360.
Clokie, Trevor
Lidbetter, Thomas F.
Molina Lovett, Antonio
Shallit, Jeffrey
and
Witzman, Leon
2022.
Computational aspects of sturdy and flimsy numbers.
Theoretical Computer Science,
Vol. 927,
Issue. ,
p.
65.