No CrossRef data available.
Article contents
AN ANALOGUE OF THE SCHUR–SIEGEL–SMYTH TRACE PROBLEM
Published online by Cambridge University Press: 30 August 2022
Abstract
By analogy with the trace of an algebraic integer
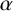 $\alpha $
with conjugates
$\alpha $
with conjugates
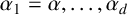 $\alpha _1=\alpha , \ldots , \alpha _d$
, we define the G-measure
$\alpha _1=\alpha , \ldots , \alpha _d$
, we define the G-measure
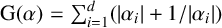 $ {\mathrm {G}} (\alpha )= \sum _{i=1}^d ( |\alpha _i| + 1/ | \alpha _i | )$
and the absolute
$ {\mathrm {G}} (\alpha )= \sum _{i=1}^d ( |\alpha _i| + 1/ | \alpha _i | )$
and the absolute
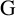 ${\mathrm G}$
-measure
${\mathrm G}$
-measure
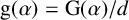 ${\mathrm {g}}(\alpha )={\mathrm {G}}(\alpha )/d$
. We establish an analogue of the Schur–Siegel–Smyth trace problem for totally positive algebraic integers. Then we consider the case where
${\mathrm {g}}(\alpha )={\mathrm {G}}(\alpha )/d$
. We establish an analogue of the Schur–Siegel–Smyth trace problem for totally positive algebraic integers. Then we consider the case where
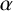 $\alpha $
has all its conjugates in a sector
$\alpha $
has all its conjugates in a sector
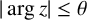 $| \arg z | \leq \theta $
,
$| \arg z | \leq \theta $
,
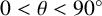 $0 < \theta < 90^{\circ }$
. We compute the greatest lower bound
$0 < \theta < 90^{\circ }$
. We compute the greatest lower bound
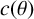 $c(\theta )$
of the absolute G-measure of
$c(\theta )$
of the absolute G-measure of
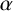 $\alpha $
, for
$\alpha $
, for
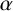 $\alpha $
belonging to
$\alpha $
belonging to
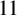 $11$
consecutive subintervals of
$11$
consecutive subintervals of
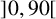 $]0, 90 [$
. This phenomenon appears here for the first time, conforming to a conjecture of Rhin and Smyth on the nature of the function
$]0, 90 [$
. This phenomenon appears here for the first time, conforming to a conjecture of Rhin and Smyth on the nature of the function
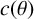 $c(\theta )$
. All computations are done by the method of explicit auxiliary functions.
$c(\theta )$
. All computations are done by the method of explicit auxiliary functions.
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.



