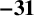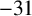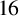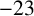The Ramanujan tau function
![]() $\tau $
is defined by
$\tau $
is defined by
 $$ \begin{align*} \Delta(z):=q \prod_{n=1}^{\infty} (1-q^{n})^{24} = \sum_{n=1}^{\infty} \tau(n) q^{n}, \end{align*} $$
$$ \begin{align*} \Delta(z):=q \prod_{n=1}^{\infty} (1-q^{n})^{24} = \sum_{n=1}^{\infty} \tau(n) q^{n}, \end{align*} $$
where
![]() $q:=e^{2 \pi i z}$
(
$q:=e^{2 \pi i z}$
(
![]() $z \in \mathbb {C}$
, Im
$z \in \mathbb {C}$
, Im
![]() $(z)>0$
). In 1930, Wilton [Reference Wilton5] determined
$(z)>0$
). In 1930, Wilton [Reference Wilton5] determined
![]() $\tau (n)$
modulo
$\tau (n)$
modulo
![]() $23$
for all positive integers n. In 2006, Sun and Williams [Reference Sun and Williams3, Corollary 2.2, page 357] obtained Wilton’s congruence for
$23$
for all positive integers n. In 2006, Sun and Williams [Reference Sun and Williams3, Corollary 2.2, page 357] obtained Wilton’s congruence for
![]() $\tau (n)$
modulo
$\tau (n)$
modulo
![]() $23$
as a consequence of their work on binary quadratic forms. Recently Dr. Pieter Moree of the Max Planck Institute for Mathematics in Bonn, Germany, in relation to his recent work [Reference Ciolan, Languasco and Moree1] with Ciolan and Languasco, asked the second author if the analogous congruence modulo
$23$
as a consequence of their work on binary quadratic forms. Recently Dr. Pieter Moree of the Max Planck Institute for Mathematics in Bonn, Germany, in relation to his recent work [Reference Ciolan, Languasco and Moree1] with Ciolan and Languasco, asked the second author if the analogous congruence modulo
![]() $31$
could be obtained using the ideas of [Reference Sun and Williams3] for the function
$31$
could be obtained using the ideas of [Reference Sun and Williams3] for the function
![]() $\tau _{16}(n)$
, where
$\tau _{16}(n)$
, where
 $$ \begin{align*} \Delta(z) E_{4}(z):=\sum_{n=1}^{\infty} \tau_{16}(n) q^{n} \end{align*} $$
$$ \begin{align*} \Delta(z) E_{4}(z):=\sum_{n=1}^{\infty} \tau_{16}(n) q^{n} \end{align*} $$
and
![]() $E_{4}(q)$
is the Eisenstein series
$E_{4}(q)$
is the Eisenstein series
 $$ \begin{align*} E_{4}(z) := 1+ 240 \sum_{n=1}^{\infty} \sigma_{3}(n) q^{n}. \end{align*} $$
$$ \begin{align*} E_{4}(z) := 1+ 240 \sum_{n=1}^{\infty} \sigma_{3}(n) q^{n}. \end{align*} $$
Swinnerton-Dyer [Reference Swinnerton-Dyer, Kuijk and Serre4, page 34], before giving the arguments that prove the congruence relation (3), notes that ‘there seems little prospect’ of proving this congruence using Dedekind’s eta function. In this note, we show that it can be done by giving an explicit proof of the congruence relation (3) using Dedekind’s eta function. Then we combine our results with [Reference Sun and Williams2, Theorem 10.2, page 166] to obtain the following congruence for
![]() $\tau _{16}(n)$
modulo
$\tau _{16}(n)$
modulo
![]() $31$
.
$31$
.
Theorem 1. For any positive integer n,
 $$ \begin{align*} \tau_{16}(n) \equiv \begin{cases} 0 \pmod{31} \hspace{0.5cm} \mbox{if there is a prime }p \mid n\mbox{ with }\scriptsize{\big(\tfrac{p}{31}\big) }=-1\\ \hspace{3cm} \mbox{and }\nu_{p}(n) \equiv 1\pmod{2}\mbox{, or }\scriptsize{\big(\tfrac{p}{31}\big) }=1\mbox{, }\\ \hspace{3cm} p= 2x^{2}+xy+4y^{2}\mbox{ and }\nu_{p}(n) \equiv 2 \pmod{3}\mbox{,}\\ \hspace{2cm} \mbox{ }\\ \displaystyle (-1)^{\mu} \hspace{-15pt}\prod_{\substack{p \mid n,\\ \scriptsize{(\frac{p}{31}) }=1,\\ p= x^{2}+xy+8y^{2}}}\hspace{-15pt} (1+ \nu_{p}(n)) \pmod{31} \hspace{0.5cm} \mbox{otherwise,} \end{cases} \end{align*} $$
$$ \begin{align*} \tau_{16}(n) \equiv \begin{cases} 0 \pmod{31} \hspace{0.5cm} \mbox{if there is a prime }p \mid n\mbox{ with }\scriptsize{\big(\tfrac{p}{31}\big) }=-1\\ \hspace{3cm} \mbox{and }\nu_{p}(n) \equiv 1\pmod{2}\mbox{, or }\scriptsize{\big(\tfrac{p}{31}\big) }=1\mbox{, }\\ \hspace{3cm} p= 2x^{2}+xy+4y^{2}\mbox{ and }\nu_{p}(n) \equiv 2 \pmod{3}\mbox{,}\\ \hspace{2cm} \mbox{ }\\ \displaystyle (-1)^{\mu} \hspace{-15pt}\prod_{\substack{p \mid n,\\ \scriptsize{(\frac{p}{31}) }=1,\\ p= x^{2}+xy+8y^{2}}}\hspace{-15pt} (1+ \nu_{p}(n)) \pmod{31} \hspace{0.5cm} \mbox{otherwise,} \end{cases} \end{align*} $$
where
 $$ \begin{align*} \mu= \hspace{-20pt}\sum_{\substack{p \mid n,\\ \scriptsize{(\frac{p}{31}) }=1,\\ p= 2x^{2}+xy+4y^{2},\\ \nu_{p}(n) \equiv 1 \pmod{3}}}\hspace{-20pt} 1. \end{align*} $$
$$ \begin{align*} \mu= \hspace{-20pt}\sum_{\substack{p \mid n,\\ \scriptsize{(\frac{p}{31}) }=1,\\ p= 2x^{2}+xy+4y^{2},\\ \nu_{p}(n) \equiv 1 \pmod{3}}}\hspace{-20pt} 1. \end{align*} $$
Proof. We use the Dedekind eta function which is defined by
 $$ \begin{align*} \eta(z):=q^{1/24} \prod_{n=1}^{\infty} (1-q^{n}). \end{align*} $$
$$ \begin{align*} \eta(z):=q^{1/24} \prod_{n=1}^{\infty} (1-q^{n}). \end{align*} $$
We have
 $$ \begin{align*} \Delta(z) E_{4}(z) &= \frac{\eta^{32}(z) \eta^{32}(4z)}{\eta^{32}(2z)} + \frac{1}{2}\bigg( \frac{\eta^{64}(2z)}{\eta^{32}(4z)} - \frac{\eta^{64}(z)}{\eta^{32}(2z)} \bigg) \\[6pt] &\quad + 31 \bigg( 69271552 \frac{\eta^{64}(4z)}{\eta^{32}(2z)} -34095104 \frac{\eta^{48}(4z)}{\eta^{8}(z)\eta^{8}(2z)} + 7915008 \frac{\eta^{16}(2z)\eta^{32}(4z)}{\eta^{16}(z)} \\[6pt] &\quad -1050688 \frac{\eta^{40}(2z)\eta^{16}(4z)}{\eta^{24}(z)} + 82977 \frac{\eta^{64}(2z)}{\eta^{32}(z)} -3840 \frac{\eta^{88}(2z)}{\eta^{40}(z)\eta^{16}(4z)}\\[6pt] &\quad + 96 \frac{\eta^{112}(2z)}{\eta^{48}(z)\eta^{32}(4z)} - \frac{\eta^{136}(2z)}{\eta^{56}(z)\eta^{48}(4z)} \bigg). \end{align*} $$
$$ \begin{align*} \Delta(z) E_{4}(z) &= \frac{\eta^{32}(z) \eta^{32}(4z)}{\eta^{32}(2z)} + \frac{1}{2}\bigg( \frac{\eta^{64}(2z)}{\eta^{32}(4z)} - \frac{\eta^{64}(z)}{\eta^{32}(2z)} \bigg) \\[6pt] &\quad + 31 \bigg( 69271552 \frac{\eta^{64}(4z)}{\eta^{32}(2z)} -34095104 \frac{\eta^{48}(4z)}{\eta^{8}(z)\eta^{8}(2z)} + 7915008 \frac{\eta^{16}(2z)\eta^{32}(4z)}{\eta^{16}(z)} \\[6pt] &\quad -1050688 \frac{\eta^{40}(2z)\eta^{16}(4z)}{\eta^{24}(z)} + 82977 \frac{\eta^{64}(2z)}{\eta^{32}(z)} -3840 \frac{\eta^{88}(2z)}{\eta^{40}(z)\eta^{16}(4z)}\\[6pt] &\quad + 96 \frac{\eta^{112}(2z)}{\eta^{48}(z)\eta^{32}(4z)} - \frac{\eta^{136}(2z)}{\eta^{56}(z)\eta^{48}(4z)} \bigg). \end{align*} $$
All of the functions in this modular equation are in
![]() $M_{16}(\Gamma _{0}(4))$
and the identity can be proved using Sturm’s theorem. Thus, we have
$M_{16}(\Gamma _{0}(4))$
and the identity can be proved using Sturm’s theorem. Thus, we have
 $$ \begin{align} \Delta(z) E_{4}(z) \equiv \frac{\eta^{32}(z) \eta^{32}(4z)}{\eta^{32}(2z)} + \frac{1}{2}\bigg( \frac{\eta^{64}(2z)}{\eta^{32}(4z)} - \frac{\eta^{64}(z)}{\eta^{32}(2z)} \bigg) \ \pmod{31}. \end{align} $$
$$ \begin{align} \Delta(z) E_{4}(z) \equiv \frac{\eta^{32}(z) \eta^{32}(4z)}{\eta^{32}(2z)} + \frac{1}{2}\bigg( \frac{\eta^{64}(2z)}{\eta^{32}(4z)} - \frac{\eta^{64}(z)}{\eta^{32}(2z)} \bigg) \ \pmod{31}. \end{align} $$
If
![]() $f:=ax^{2}+bxy+cy^{2}$
is a positive-definite integral binary quadratic form, we denote by
$f:=ax^{2}+bxy+cy^{2}$
is a positive-definite integral binary quadratic form, we denote by
![]() $r(f;n)$
the number of representations of a nonnegative integer n by f. We set
$r(f;n)$
the number of representations of a nonnegative integer n by f. We set
 $$ \begin{align*} \phi_{2}(z)&:=\frac{1}{2}\sum_{n \geq 0} (r(x^{2}+xy+8 y^{2};n)-r(2x^{2}+xy+4 y^{2};n)) q^{n}\\[6pt] &\ = \frac{1}{2} \sum_{x,y=-\infty}^{\infty} (q^{x^{2}+xy+8 y^{2}} - q^{2x^{2}+xy+4 y^{2}}). \end{align*} $$
$$ \begin{align*} \phi_{2}(z)&:=\frac{1}{2}\sum_{n \geq 0} (r(x^{2}+xy+8 y^{2};n)-r(2x^{2}+xy+4 y^{2};n)) q^{n}\\[6pt] &\ = \frac{1}{2} \sum_{x,y=-\infty}^{\infty} (q^{x^{2}+xy+8 y^{2}} - q^{2x^{2}+xy+4 y^{2}}). \end{align*} $$
The theta functions
![]() $\sum _{x,y=-\infty }^{\infty } q^{x^{2}+xy+8 y^{2}}$
and
$\sum _{x,y=-\infty }^{\infty } q^{x^{2}+xy+8 y^{2}}$
and
![]() $\sum _{x,y=-\infty }^{\infty } q^{2x^{2}+xy+4 y^{2}}$
belong to the space
$\sum _{x,y=-\infty }^{\infty } q^{2x^{2}+xy+4 y^{2}}$
belong to the space
![]() $M_{1}(\Gamma _{0}(124),\scriptsize {(\frac{-31}{*}) })$
as do the eta quotients
$M_{1}(\Gamma _{0}(124),\scriptsize {(\frac{-31}{*}) })$
as do the eta quotients
 $$ \begin{align*} \frac{\eta(z) \eta(4z) \eta(31z)\eta(124z)}{\eta(2z)\eta(62z)}, \quad \frac{\eta^{2}(2z)\eta^{2}(62z)}{\eta(4z)\eta(124z)} \quad\mbox{and}\quad \frac{\eta^{2}(z)\eta^{2}(31z)}{\eta(2z)\eta(62z)}. \end{align*} $$
$$ \begin{align*} \frac{\eta(z) \eta(4z) \eta(31z)\eta(124z)}{\eta(2z)\eta(62z)}, \quad \frac{\eta^{2}(2z)\eta^{2}(62z)}{\eta(4z)\eta(124z)} \quad\mbox{and}\quad \frac{\eta^{2}(z)\eta^{2}(31z)}{\eta(2z)\eta(62z)}. \end{align*} $$
Then it is straightforward to prove the modular identity
 $$ \begin{align*} \phi_{2}(z) = \frac{\eta(z) \eta(4z) \eta(31z)\eta(124z)}{\eta(2z)\eta(62z)} + \frac{1}{2}\bigg( \frac{\eta^{2}(2z)\eta^{2}(62z)}{\eta(4z)\eta(124z)} - \frac{\eta^{2}(z)\eta^{2}(31z)}{\eta(2z)\eta(62z)} \bigg) \end{align*} $$
$$ \begin{align*} \phi_{2}(z) = \frac{\eta(z) \eta(4z) \eta(31z)\eta(124z)}{\eta(2z)\eta(62z)} + \frac{1}{2}\bigg( \frac{\eta^{2}(2z)\eta^{2}(62z)}{\eta(4z)\eta(124z)} - \frac{\eta^{2}(z)\eta^{2}(31z)}{\eta(2z)\eta(62z)} \bigg) \end{align*} $$
using Sturm’s theorem. We have
![]() $1-A^{31} \equiv (1-A)^{31}$
(mod
$1-A^{31} \equiv (1-A)^{31}$
(mod
![]() $31$
) by the binomial theorem, so that
$31$
) by the binomial theorem, so that
 $$ \begin{align} \phi_{2}(z) \equiv \frac{\eta^{32}(z) \eta^{32}(4z)}{\eta^{32}(2z)} + \frac{1}{2}\bigg( \frac{\eta^{64}(2z)}{\eta^{32}(4z)} - \frac{\eta^{64}(z)}{\eta^{32}(2z)} \bigg) \ \pmod{31}. \end{align} $$
$$ \begin{align} \phi_{2}(z) \equiv \frac{\eta^{32}(z) \eta^{32}(4z)}{\eta^{32}(2z)} + \frac{1}{2}\bigg( \frac{\eta^{64}(2z)}{\eta^{32}(4z)} - \frac{\eta^{64}(z)}{\eta^{32}(2z)} \bigg) \ \pmod{31}. \end{align} $$
From (1) and (2), we deduce that
Appealing to the formula for
![]() $\tfrac 12(r(x^{2}+xy+8 y^{2};n)-r(2x^{2}+xy+4 y^{2};n))$
given in [Reference Sun and Williams2, Theorem 10.2, page 166], we obtain from (3) the congruence for
$\tfrac 12(r(x^{2}+xy+8 y^{2};n)-r(2x^{2}+xy+4 y^{2};n))$
given in [Reference Sun and Williams2, Theorem 10.2, page 166], we obtain from (3) the congruence for
![]() $\tau _{16}(n)$
stated in the theorem.
$\tau _{16}(n)$
stated in the theorem.