Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T21:39:09.896Z Has data issue: false hasContentIssue false
  • English
  • Français

AN APPLICATION OF SCHUR’S ALGORITHM TO VARIABILITY REGIONS OF CERTAIN ANALYTIC FUNCTIONS II

Part of: Geometric function theory

Published online by Cambridge University Press:  02 December 2021

MD FIROZ ALI ,
VASUDEVARAO ALLU  and
HIROSHI YANAGIHARA
MD FIROZ ALI
Affiliation:
Department of Mathematics, NIT Durgapur, Mahatma Gandhi Avenue, Durgapur 713209, West Bengal, India e-mail: ali.firoz89@gmail.com; firoz.ali@maths.nitdgp.ac.in
VASUDEVARAO ALLU*
Affiliation:
Discipline of Mathematics, School of Basic Sciences, Indian Institute of Technology Bhubaneswar, Argul, Bhubaneswar, Khordha 752050, Odisha, India
HIROSHI YANAGIHARA
Affiliation:
Department of Applied Science, Faculty of Engineering, Yamaguchi University, Tokiwadai, Ube 755, Japan e-mail: hiroshi@yamaguchi-u.ac.jp
*
e-mail: avrao@iitbbs.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

We extend our study of variability regions, Ali et al. [‘An application of Schur algorithm to variability regions of certain analytic functions–I’, Comput. Methods Funct. Theory, to appear] from convex domains to starlike domains. Let 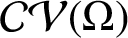$\mathcal {CV}(\Omega )$ be the class of analytic functions f in 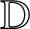${\mathbb D}$ with 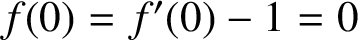$f(0)=f'(0)-1=0$ satisfying 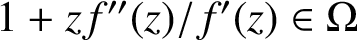$1+zf''(z)/f'(z) \in {\Omega }$ . As an application of the main result, we determine the variability region of 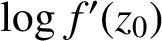$\log f'(z_0)$ when f ranges over 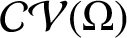$\mathcal {CV}(\Omega )$ . By choosing a particular $\Omega $ , we obtain the precise variability regions of 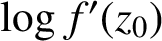$\log f'(z_0)$ for some well-known subclasses of analytic and univalent functions.

Keywords

analytic functionunivalent functionconvex functionstarlike functionBanach spacenormSchur algorithmsubordinationvariability region

MSC classification

Primary: 30C45: Special classes of univalent and multivalent functions (starlike, convex, bounded rotation, etc.)
Secondary: 30C75: Extremal problems for conformal and quasiconformal mappings, other methods
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 105 , Issue 3 , June 2022 , pp. 468 - 481
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The second author thanks SERB-MATRICS for financial support.

References

Ali, M. F. and Vasudevarao, A., ‘Coefficient inequalities and Yamashita’s conjecture for some classes of analytic functions’, J. Aust. Math. Soc. 100 (2016), 1–20.CrossRefGoogle Scholar
Ali, M. F., Allu, V. and Yanagihara, H., ‘An application of Schur algorithm to variability regions of certain analytic functions – I’, Comput. Methods Funct. Theory. doi:10.1007/s40315-021-00362-z.CrossRefGoogle Scholar
Bakonyi, M. and Constantinescu, T., Schur’s Algorithm and Several Applications, Pitman Research Notes in Mathematics, 261 (Longman Scientific and Technical, Harlow, Essex, 1992).Google Scholar
Duren, P., Univalent Functions, Grundlehren der mathematischen Wissenschaften, 259 (Springer, New York 1983).Google Scholar
Finkelstein, M., ‘Growth estimates of convex functions’, Proc. Amer. Math. Soc. 18 (1967), 412–418.Google Scholar
Foias, C. and Frazho, A. E., The Commutant Lifting Approach to Interpolation Problems, Operator Theory: Advances and Applications, 44 (Birkhäuser, Basel, 1990).Google Scholar
Gronwall, T. H., ‘On the distortion in conformal mapping when the second coefficient in the mapping function has an assigned value’, Proc. Natl. Acad. Sci. USA 6 (1920), 300–302.CrossRefGoogle ScholarPubMed
Hallenbeck, D. J. and Ruscheweyh, S., ‘Subordination by convex functions’, Proc. Amer. Math. Soc. 52 (1975), 191–195.CrossRefGoogle Scholar
Janowski, W., ‘Some extremal problems for certain families of analytic functions’, Ann. Polon. Math. 28 (1973), 297–326.CrossRefGoogle Scholar
Kanas, S. and Wiśniowska, A., ‘Conic regions and $k$ -uniform convexity’, J. Comput. Appl. Math. 105 (1999), 327–336.CrossRefGoogle Scholar
Ponnusamy, S. and Vasudevarao, A., ‘Region of variability of two subclasses of univalent functions’, J. Math. Anal. Appl. 332 (2007), 1323–1334.Google Scholar
Ponnusamy, S., Sahoo, S. K. and Yanagihara, H., ‘Radius of convexity of partial sums of functions in the close-to-convex family’, Nonlinear Anal. 95 (2014), 219–228.CrossRefGoogle Scholar
Ponnusamy, S., Vasudevarao, A. and Yanagihara, H., ‘Region of variability of univalent functions $f(z)$ for which $z{f}^{\prime }(z)$ is spirallike’, Houston J. Math. 34 (2008), 1037–1048.Google Scholar
Ronning, F., ‘A survey in uniformly convex and uniformly starlike functions’, Ann. Univ. Mariae Curie-Sklodowska Sect. A 47 (1993), 123–134.Google Scholar
Schur, I., ‘Über Potenzreihen, die im Innern des Einheitskreises beschränkt sind’, J. reine angew. Math. 147 (1917), 205–232.CrossRefGoogle Scholar
Schur, I., ‘On power series which are bounded in the interior of the unit circle I’, in: Schur Methods in Operator Theory and Signal Processing, Operator Theory: Advances and Applications, 18 (ed. Gohberg, I.) (Birkhäuser, Basel, 1986), 31–59, translated from the German by I. Gohberg.CrossRefGoogle Scholar
Suffridge, T. J., ‘Some remarks on convex maps of the unit disk’, Duke Math. J. 37 (1970), 755–777.Google Scholar
Ul-Haq, W., ‘Variability regions for Janowski convex functions’, Complex Var. Elliptic Equ. 59 (2014), 355–361.CrossRefGoogle Scholar
Yanagihara, H., ‘Regions of variability for functions of bounded derivatives’, Kodai Math. J. 28 (2005), 452–462.CrossRefGoogle Scholar
Yanagihara, H., ‘Regions of variability for convex functions’, Math. Nachr. 279 (2006), 1723–1730.CrossRefGoogle Scholar
Yanagihara, H., ‘Variability regions for families of convex functions’, Comput. Methods Funct. Theory 10 (2010), 291–302.Google Scholar