Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-26T19:00:06.223Z Has data issue: false hasContentIssue false
  • English
  • Français

An existence theorem for the generalized complementarity problem

Published online by Cambridge University Press:  17 April 2009

J. Parida  and
B. Sahoo
J. Parida
Affiliation:
Department of Mathematics, Regional Engineering College, Rourkela, Orissa, India.
B. Sahoo
Affiliation:
Department of Mathematics, Regional Engineering College, Rourkela, Orissa, India.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a closed, convex cone S, in Rn, its polar S* and a mapping g from Rn into itself, the generalized nonlinear complementarity problem is to find a z ∈ Rn such that

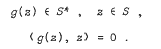
Many existence theorems for the problem have been established under varying conditions on g. We introduce new mappings, denoted by J(S)-functions, each of which is used to guarantee the existence of a solution to the generalized problem under certain coercivity conditions on itself. A mapping g:S → Rn is a J(S)-function if

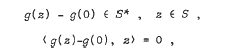
imply that z = 0. It is observed that the new class of functions is a broader class than the previously studied ones.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 19 , Issue 1 , August 1978 , pp. 51 - 58
Copyright
Copyright © Australian Mathematical Society 1979

References

[1]Bazaraa, M.S. and Goode, J.J., “Necessary optimality criteria in mathematical programming in the presence of differentiability”, J. Math. Anal. Appl. 40 (1972), 609–621.CrossRefGoogle Scholar
[2]Habetler, G.J. and Price, A.L., “Existence theory for generalized non-linear complementarity problems”, J. Optimization Theory Appl. 1 (1971), 223–239.CrossRefGoogle Scholar
[3]Karamardian, S., “Generalized complementarity problem”, J. Optimization Theory Appl. 8 (1971), 161–168.CrossRefGoogle Scholar
[4]Karamardian, S., “The complementarity problem”, Math. Programming 2 (1972), 107–129.CrossRefGoogle Scholar
[5]Karamardian, S., “An existence theorem for the complementarity problem”, J. Optimization Theory Appl. 19 (1976), 227–232.CrossRefGoogle Scholar
[6]Moré, Jorge J., “Coercivity conditions in nonlinear complementarity problems”, SIAM Rev. 16 (1974), 1–16.CrossRefGoogle Scholar
[7]Parida, J. and Sahoo, B., “A note on generalised linear complementarity problems”, Bull. Austral. Math. Soc. 18 (1978), 161–168.CrossRefGoogle Scholar