Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T05:00:59.584Z Has data issue: false hasContentIssue false
  • English
  • Français

An interpolation by successive derivatives at a finite set

Published online by Cambridge University Press:  17 April 2009

Soon-Yeong Chung
Soon-Yeong Chung
Affiliation:
Department of Mathematics, Sogang University, Seoul 121-742, Korea e-mail: sychung@ccs.sogang.ac.kr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For an n-times differentiable function f(x) whose derivatives f(j)(xj) at x = xj, j = 0, 1, …, n are specified, we introduce a sequence of fundamental polynomials 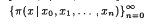to interpolate f(x) with a remainder as

The remainder R(x|x0, x1,… xn) is given in an integral form and Lagrange's form.

In addition, by introducing orthogonality of Sobolev type we verify the best optimality of the approximations and interpret the fundamental polynomials as a kind of Sobolev orthogonal polynomial.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 58 , Issue 3 , December 1998 , pp. 513 - 524
Copyright
Copyright © Australian Mathematical Society 1998

References

[1]Davis, P.J., Interpolation and approximation (Blaisdell, New York, Toronto, London, 1963).Google Scholar
[2]Jung, I.H., Kwon, K.H., and Littlejohn, L.L., ‘Sobolev orthogonal polynomials and spectral differential equations’, Trans. Amer. Math. Soc. 347 (1995), p. 3629–3643.CrossRefGoogle Scholar