Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T06:30:57.900Z Has data issue: false hasContentIssue false
  • English
  • Français

AN OPEN MAPPING THEOREM

Part of: Topological linear spaces and related structures Topological and differentiable algebraic systems

Published online by Cambridge University Press:  08 January 2016

SAAK S. GABRIYELYAN  and
SIDNEY A. MORRIS
SAAK S. GABRIYELYAN
Affiliation:
Department of Mathematics, Ben-Gurion University of the Negev, PO Box 653, Beer-Sheva, Israel email saak@math.bgu.ac.il
SIDNEY A. MORRIS*
Affiliation:
Faculty of Science and Technology, Federation University Australia, PO Box 663, Ballarat, Victoria 3353, Australia Department of Mathematics and Statistics, La Trobe University, Melbourne, Victoria 3086, Australia email morris.sidney@gmail.com
*
✉saak@math.bgu.ac.il
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is proved that any surjective morphism 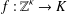$f:\mathbb{Z}^{{\it\kappa}}\rightarrow K$ onto a locally compact group 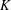$K$ is open for every cardinal ${\it\kappa}$. This answers a question posed by Hofmann and the second author.

Keywords

pro-Lie grouplocally compact abelian groupopen mapping theorem

MSC classification

Primary: 22A05: Structure of general topological groups
Secondary: 46A30: Open mapping and closed graph theorems; completeness (including $B$-, $B_r$-completeness)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 1 , August 2016 , pp. 65 - 69
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Balcerzyk, S., ‘On the algebraically compact groups of I. Kaplansky’, Fund. Math. 44 (1957), 91–93.CrossRefGoogle Scholar
Fabian, M., Habala, P., Hájek, P., Montesinos, V., Pelan, J. and Zizler, V., Banach Space Theory. The Basis for Linear and Nonlinear Analysis (Springer, New York, 2010).Google Scholar
Hewitt, E. and Ross, K. A., Abstract Harmonic Analysis, 2nd edn, Vol. I (Springer, Berlin, 1979).CrossRefGoogle Scholar
Hofmann, K. H. and Morris, S. A., ‘An open mapping theorem for pro-lie groups’, J. Aust. Math. Soc. 83 (2007), 55–77.CrossRefGoogle Scholar
Hofmann, K. H. and Morris, S. A., The Lie Theory of Connected Pro-Lie Groups (EMS Publishing House, Zürich, 2007).CrossRefGoogle Scholar
Hofmann, K. H. and Morris, S. A., ‘The structure of almost connected pro-Lie groups’, J. Lie Theory 21 (2011), 347–383.Google Scholar
Hofmann, K. H. and Morris, S. A., ‘Pro-Lie groups: a survey with open problems’, Axioms 4 (2015), 294–312.CrossRefGoogle Scholar
Koshi, Sh. and Takesaki, M., ‘An open mapping theorem on homogeneous spaces’, J. Aust. Math. Soc. 53 (1992), 51–54.CrossRefGoogle Scholar
Legg, M. W. and Walker, E. A., ‘An algebraic treatment of algebraically compact groups’, Rocky Mountain J. Math. 5 (1975), 291–299.CrossRefGoogle Scholar
Morris, S. A., Pontryagin Duality and the Structure of Locally Compact Abelian Groups (Cambridge University Press, Cambridge, 1977).CrossRefGoogle Scholar