Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kumar, Devendra
2011.
Generalized growth and best approximation of entire functions in L p -norm in several complex variables.
ANNALI DELL'UNIVERSITA' DI FERRARA,
Vol. 57,
Issue. 2,
p.
353.

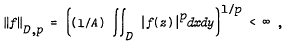 where
where 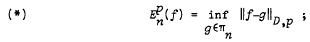
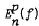 , such that
, such that 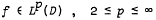 has an analytic continuation as an entire function having finite order and finite type. In the present paper we have considered the approximation error (*) on a Carathéodory domain and have extended the results of Giroux for the case 1 ≤ p < 2.
has an analytic continuation as an entire function having finite order and finite type. In the present paper we have considered the approximation error (*) on a Carathéodory domain and have extended the results of Giroux for the case 1 ≤ p < 2.