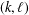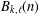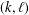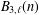Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zhang, Wenlong
and
Shi, Ji
2019.
Congruences for the coefficients of the mock theta function $$\beta (q)$$ β ( q ).
The Ramanujan Journal,
Vol. 49,
Issue. 2,
p.
257.
Tang, Dazhao
2020.
Arithmetic properties for two restricted partitions modulo powers of 5.
Quaestiones Mathematicae,
Vol. 43,
Issue. 2,
p.
169.
Ray, Chiranjit
and
Barman, Rupam
2020.
On Andrews' integer partitions with even parts below odd parts.
Journal of Number Theory,
Vol. 215,
Issue. ,
p.
321.
Ray, Chiranjit
and
Barman, Rupam
2020.
Arithmetic properties of cubic and overcubic partition pairs.
The Ramanujan Journal,
Vol. 52,
Issue. 2,
p.
243.
DA SILVA, ROBSON
and
SELLERS, JAMES A.
2021.
ARITHMETIC PROPERTIES OF 3-REGULAR PARTITIONS IN THREE COLOURS.
Bulletin of the Australian Mathematical Society,
Vol. 104,
Issue. 3,
p.
415.
Kathiravan, T.
2022.
Ramanujan-type congruences modulo m for (l, m)-regular bipartitions .
Indian Journal of Pure and Applied Mathematics,
Vol. 53,
Issue. 2,
p.
375.
Ray, Chiranjit
and
Chakraborty, Kalyan
2022.
Certain eta-quotients and $$\ell $$-regular overpartitions.
The Ramanujan Journal,
Vol. 57,
Issue. 2,
p.
453.
SINGH, AJIT
and
BARMAN, RUPAM
2022.
PROOF OF SOME CONJECTURAL CONGRUENCES OF DA SILVA AND SELLERS.
Bulletin of the Australian Mathematical Society,
Vol. 106,
Issue. 1,
p.
57.
Singh, Ajit
and
Barman, Rupam
2022.
Divisibility of certain $$\ell $$-regular partitions by 2.
The Ramanujan Journal,
Vol. 59,
Issue. 3,
p.
813.
Jindal, Ankita
and
Meher, N K
2023.
Arithmetic density and new congruences for $$\pmb 3$$-core partitions.
Proceedings - Mathematical Sciences,
Vol. 133,
Issue. 2,
Ballantine, Cristina
and
Merca, Mircea
2023.
Congruences modulo 4 for the number of 3-regular partitions.
Comptes Rendus. Mathématique,
Vol. 361,
Issue. G9,
p.
1577.
Baruah, Nayandeep Deka
and
Das, Hirakjyoti
2023.
Congruences for the coefficients of a pair of third and sixth order mock theta functions.
The Ramanujan Journal,
Vol. 61,
Issue. 4,
p.
1269.
Baruah, Nayandeep Deka
Das, Hirakjyoti
and
Talukdar, Pranjal
2023.
Congruences for k-elongated plane partition diamonds.
International Journal of Number Theory,
Vol. 19,
Issue. 09,
p.
2121.
Palani, Murugan
and
Fathima, Syeda Noor
2024.
Ramanujan-Type Congruences for $$(\ell ,m)$$-Regular Bipartitions Modulo 2, 5 and 7.
Vietnam Journal of Mathematics,
Jindal, Ankita
and
Meher, N. K.
2024.
Arithmetic Density and Congruences of t-Core Partitions.
Results in Mathematics,
Vol. 79,
Issue. 1,
Das, Hirakjyoti
2025.
Congruences between the coefficients of certain mock theta functions.
Journal of Mathematical Analysis and Applications,
Vol. 543,
Issue. 2,
p.
128913.
Meher, Nabin Kumar
2025.
Distribution and congruences of $$\ell $$-regular bipartitions.
Rendiconti del Circolo Matematico di Palermo Series 2,
Vol. 74,
Issue. 1,