Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fathi, Ali
Tehranian, Abolfazl
and
Zakeri, Hossein
2015.
Filter Regular Sequences and Generalized Local Cohomology Modules.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 38,
Issue. 2,
p.
467.
Rahimpour Nasbi, Yashar
Vahidi, Alireza
and
Ahmadi Amoli, Khadijeh
2017.
Torsion functors of generalized local cohomology modules.
Communications in Algebra,
Vol. 45,
Issue. 12,
p.
5420.
Jorge Pérez, V. H.
and
Merighe, L. C.
2020.
On a question of D. Rees on classical integral closure and integral closure relative to an Artinian module.
Journal of Algebra and Its Applications,
Vol. 19,
Issue. 02,
p.
2050033.
Hasanzad, Masoumeh
and
A’zami, Jafar
2020.
A short note on annihilators of local cohomology modules.
Journal of Algebra and Its Applications,
Vol. 19,
Issue. 02,
p.
2050026.
Nam, Nguyen Thanh
Nam, Tran Tuan
and
Tri, Nguyen Minh
2021.
On Minimax Modules and Generalized Local Cohomology with Respect to a Pair of Ideals.
Acta Mathematica Vietnamica,
Vol. 46,
Issue. 3,
p.
457.
Carsava Merighe, Liliam
2022.
Counting the number of non-isomorphic top generalized local cohomology modules.
Latin American Journal of Mathematics,
Vol. 1,
Issue. 01,
p.
1.
Shen, Jingwen
and
Yang, Xiaoyan
2023.
The $$\mathfrak a$$-filter Grade of an Ideal $$\mathfrak b$$ and $$(\mathfrak a,\mathfrak b)$$-f-modules.
Frontiers of Mathematics,
Vol. 18,
Issue. 2,
p.
503.


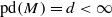 ,
, 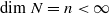 . First, we give the formula for the attached primes of the top generalized local cohomology module
. First, we give the formula for the attached primes of the top generalized local cohomology module 