Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-27T19:43:59.022Z Has data issue: false hasContentIssue false
  • English
  • Français

The average distance property of classical Banach spaces

Published online by Cambridge University Press:  17 April 2009

Aicke Hinrichs
Aicke Hinrichs
Affiliation:
Mathematisches Institut, FSU Jena, D 07743 JenaGermany e-mail: nah@rz.uni-jena.de Current address: Department of Mathematics, Texas A&M University, College Station, TX 77843, United States of America
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A Banach space X has the average distance property (ADP) if there exists a unique real number r such that for each positive integer n and all x1,…,xn in the unit sphere of X there is some x in the unit sphere of X such that .

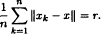It is known that l2 and l∞ have the ADP, whereas lp fails to have the ADP if 1 ≤ p < 2. We show that lp also fails to have the ADP for 3 ≤ p ≤ ∞. Our method seems to be able to decide also the case 2 < p < 3, but the computational difficulties increase as p comes closer to 2.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 62 , Issue 1 , August 2000 , pp. 119 - 134
Copyright
Copyright © Australian Mathematical Society 2000

References

[1]Cleary, J., Morris, A. and Yost, D., ‘Numerical geometry – numbers for shapes’, Amer. Math. Monthly 93 (1986), 260–275.CrossRefGoogle Scholar
[2]Gross, O., ‘The rendezvous value of a metric space’, Ann. of Math. Stud. 52 (1964), 49–53.Google Scholar
[3]Hinrichs, A., ‘Details of some computations on the average distance property of Lp’, http://www.minet.uni-jena.de/~hinrichs/adpcomp/.Google Scholar
[4]Morris, S.A. and Nickolas, P., ‘On the average distance property of compact connected metric spaces’, Arch. Math. 40 (1983), 459–463.CrossRefGoogle Scholar
[5]Lin, P.K., ‘The average distance property of Banach spaces’, Arch. Math. 68 (1997), 496–502.CrossRefGoogle Scholar
[6]Wolf, R., ‘On the average distance property of spheres in Banach spaces’, Arch. Math. 62 (1994), 338–344.CrossRefGoogle Scholar