Published online by Cambridge University Press: 17 April 2009
Let E be a Banach space. The averaging interval AI(E) is defined as the set of positive real numbers α, with the following property: For each n ∈ ℕ and for all (not necessarily distinct) x1, x2, … xn ∈ E with ∥x1∥ = ∥x2∥ = … = ∥xn∥ = 1, there is an x ∈ E, ∥x∥ = 1, such that
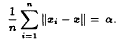
It follows immediately, that AI(E) is a (perhaps empty) interval included in the closed interval [1,2]. For example in this paper it is shown that AI(E) = {α} for some 1 < α < 2, if E has finite dimension. Furthermore a complete discussion of AI(C(X)) is given, where C(X) denotes the Banach space of real valued continuous functions on a compact Hausdorff space X. Also a Banach space E is found, such that AI(E) = [1,2].