Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T12:58:39.469Z Has data issue: false hasContentIssue false
  • English
  • Français

BIASES IN INTEGER PARTITIONS

Part of: Additive number theory; partitions Combinatorics

Published online by Cambridge University Press:  14 January 2021

BYUNGCHAN KIM Open the ORCID record for BYUNGCHAN KIM [Opens in a new window]  and
EUNMI KIM Open the ORCID record for EUNMI KIM [Opens in a new window]
BYUNGCHAN KIM
Affiliation:
School of Liberal Arts, Seoul National University of Science and Technology, 232 Gongneung-ro, Nowon-gu, Seoul1811, Republic of Korea e-mail: bkim4@seoultech.ac.kr
EUNMI KIM*
Affiliation:
Institute of Mathematical Sciences, Ewha Womans University, 52 Ewhayeodae-gil, Seodaemun-gu, Seoul03760, Republic of Korea
*
e-mail: ekim67@ewha.ac.kr
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that there are biases in the number of appearances of the parts in two residue classes in the set of ordinary partitions. More precisely, let 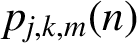$p_{j,k,m} (n)$ be the number of partitions of n such that there are more parts congruent to j modulo m than parts congruent to k modulo m for 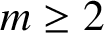$m \geq 2$ . We prove that 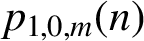$p_{1,0,m} (n)$ is in general larger than 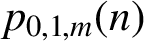$p_{0,1,m} (n)$ . We also obtain asymptotic formulas for 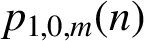$p_{1,0,m}(n)$ and 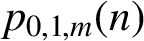$p_{0,1,m}(n)$ for 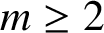$m \geq 2$ .

Keywords

asymptotic formulabiaspartition

MSC classification

Primary: 05A17: Partitions of integers
Secondary: 11P81: Elementary theory of partitions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 104 , Issue 2 , October 2021 , pp. 177 - 186
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Byungchan Kim was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT (NRF-2019R1F1A1043415); Eunmi Kim was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF–2020R1I1A1A01065877, NRF–2019R1A6A1A11051177).

References

Alder, H. L., ‘The nonexistence of certain identities in the theory of partitions and compositions’, Bull. Amer. Math. Soc. 54 (1948), 712–722.CrossRefGoogle Scholar
Alfes, C., Jameson, M. and Lemke Oliver, R. J., ‘Proof of the Alder–Andrews conjecture’, Proc. Amer. Math. Soc. 139(1) (2011), 63–78.CrossRefGoogle Scholar
Andrews, G. E., ‘On a partition problem of H. L. Alder’, Pacific. J. Math. 36 (1971), 279–284.CrossRefGoogle Scholar
Andrews, G. E., ‘Difference of partition functions: the anti-telescoping method’, in: From Fourier Analysis and Number Theory to Radon Transforms and Geometry, Developments in Mathematics, 28 (Springer, New York, 2013), 1–20.CrossRefGoogle Scholar
Berkovich, A. and Grizzell, K., ‘Races among products’, J. Combin. Theory Ser. A 119(8) (2012), 1789–1797.CrossRefGoogle Scholar
Berkovich, A. and Grizzell, K., ‘A partition inequality involving products of two $q$ -Pochhammer symbols’, in: Ramanujan 125, Contemporary Mathematics, 627 (American Mathematical Society, Providence, RI, 2014), 25–39.Google Scholar
Bringmann, K., Jennings-Shaffer, C. and Mahlburg, K., ‘On a Tauberian Theorem of Ingham and Euler–Maclaurin summation’, Ramanujan J., to appear.Google Scholar
Bringmann, K., Mahlburg, K. and Nataraj, K., ‘Distinct parts partitions without sequences’, Electron. J. Combin. 22 (2015), P3.31.CrossRefGoogle Scholar
Garvan, F., ‘New combinatorial interpretations of Ramanujan’s partition congruences mod $5$ , $7$ and $11$ ’, Trans. Amer. Math. Soc. 305(1) (1988), 47–77.Google Scholar
Gasper, G. and Rahman, M., Basic Hypergeometric Series, 2nd edn, Encyclopedia of Mathematics and its Applications, 96 (Cambridge University Press, Cambridge, 2004).CrossRefGoogle Scholar
Ingham, A., ‘A Tauberian theorem for partitions’, Ann. of Math. 42 (1941), 1075–1090.CrossRefGoogle Scholar
Kadell, K. W. J., ‘An injection for the Ehrenpreis Rogers–Ramanujan problem’, J. Combin. Theory Ser. A 86(2) (1999), 390–394.CrossRefGoogle Scholar
Kim, B., Kim, E. and Lovejoy, J., ‘Parity bias in partitions’, European J. Combin . 89 (2020), 103159.CrossRefGoogle Scholar
Yee, A. J., ‘Alder’s conjecture’, J. reine angew. Math. 616 (2008), 67–88.Google Scholar
Zagier, D., ‘The dilogarithm function’, in: Frontiers in Number Theory, Physics, and Geometry. II (Springer, Berlin, 2007), 3–65.CrossRefGoogle Scholar