Hostname: page-component-6bf8c574d5-b4m5d Total loading time: 0 Render date: 2025-02-21T20:31:02.089Z Has data issue: false hasContentIssue false
  • English
  • Français

BIPARTITE SUBGRAPHS OF 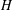$H$-FREE GRAPHS

Part of: Graph theory

Published online by Cambridge University Press:  07 February 2017

QINGHOU ZENG  and
JIANFENG HOU
QINGHOU ZENG*
Affiliation:
Center for Discrete Mathematics, Fuzhou University, Fujian, 350003, China email qinghouzeng@hotmail.com
JIANFENG HOU
Affiliation:
Center for Discrete Mathematics, Fuzhou University, Fujian, 350003, China email jfhou@fzu.edu.cn
*
✉qinghouzeng@hotmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a graph 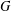$G$, let 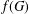$f(G)$ denote the maximum number of edges in a bipartite subgraph of 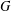$G$. For an integer 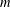$m$ and for a fixed graph 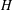$H$, let 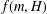$f(m,H)$ denote the minimum possible cardinality of 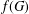$f(G)$ as 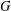$G$ ranges over all graphs on 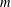$m$ edges that contain no copy of 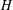$H$. We give a general lower bound for 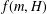$f(m,H)$ which extends a result of Erdős and Lovász and we study this function for any bipartite graph 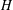$H$ with maximum degree at most 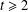$t\geq 2$ on one side.

Keywords

H-free graphpartitionbipartite subgraph

MSC classification

Primary: 05C35: Extremal problems
Secondary: 05C70: Factorization, matching, partitioning, covering and packing
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 1 , August 2017 , pp. 1 - 13
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

This work is supported by NSFC (Grant No. 11671087) and New Century Programming of Fujian Province (Grant No. JA14028).

References

Alon, N., ‘Bipartite subgraphs’, Combinatorica 16 (1996), 301–311.Google Scholar
Alon, N., Bollobás, B., Krivelevich, M. and Sudakov, B., ‘Maximum cuts and judicious partitions in graphs without short cycles’, J. Combin. Theory Ser. B 88 (2003), 329–346.CrossRefGoogle Scholar
Alon, N. and Halperin, E., ‘Bipartite subgraphs of integer weighted graphs’, Discrete Math. 181 (1998), 19–29.CrossRefGoogle Scholar
Alon, N., Krivelevich, M. and Sudakov, B., ‘Turán numbers of bipartite graphs and related Ramsey-type questions’, Combin. Probab. Comput. 12 (2003), 477–494.Google Scholar
Alon, N., Krivelevich, M. and Sudakov, B., ‘Maxcut in H-free graphs’, Combin. Probab. Comput. 14 (2005), 629–647.CrossRefGoogle Scholar
Alon, N., Rónyai, L. and Szabó, T., ‘Norm-graphs: variations and applications’, J. Combin. Theory Ser. B 76 (1999), 280–290.Google Scholar
Bollobás, B. and Scott, A. D., ‘Better bounds for Max Cut’, in: Contemporary Combinatorics, Bolyai Society Mathematical Studies, 10 (Springer, Berlin, 2002), 185–246.Google Scholar
Bollobás, B. and Scott, A. D., ‘Problems and results on judicious partitions’, Random Structures Algorithms 21 (2002), 414–430.Google Scholar
Edwards, C. S., ‘An improved lower bound for the number of edges in a largest bipartite subgraph’, in: Recent Advances in Graph Theory: Proc. 2nd Czechoslovak Sympos. Graph Theory (Academia, Praha, 1975), 167–181.Google Scholar
Erdős, P., ‘Problems and results in graph theory and combinatorial analysis’, in: Graph Theory and Related Topics: Proc. Conf. Waterloo, 1977 (Academic Press, New York, 1979), 153–163.Google Scholar
Erdős, P., Gyárfás, A. and Kohayakawa, Y., ‘The size of the largest bipartite subgraphs’, Discrete Math. 177 (1997), 267–271.Google Scholar
Janson, S., Łuczak, T. and Ruciński, A., Random Graphs (John Wiley, New York, 2000).Google Scholar
Jensen, T. R. and Toft, B., Graph Coloring Problems, Wiley-Interscience Series in Discrete Mathematics and Optimization (John Wiley, New York, 1995).Google Scholar
Kostochka, A., Sudakov, B. and Verstraëte, J., ‘Cycles in triangle-free graphs of large chromatic number’, Combinatorica doi:10.1007/s00493-015-3262-0.Google Scholar
Li, Y., Rousseau, C. and Zang, W., ‘Asymptotic upper bounds for Ramsey functions’, Graphs Combin. 17 (2001), 123–128.Google Scholar
Poljak, S. and Tuza, Zs., ‘Bipartite subgraphs of triangle-free graphs’, SIAM J. Discrete Math. 7 (1994), 307–313.Google Scholar
Scott, A. D., ‘Judicious partitions and related problems’, in: Surveys in Combinatorics, London Mathematical Society Lecture Note Series, 327 (Cambridge University Press, Cambridge, 2005), 95–117.Google Scholar
Shearer, J., ‘A note on independence number of triangle-free graphs’, Discrete Math. 46 (1983), 83–87.Google Scholar
Shearer, J., ‘A note on bipartite subgraphs of triangle-free graphs’, Random Structures Algorithms 3 (1992), 223–226.CrossRefGoogle Scholar
Shearer, J., ‘On the independence number of sparse graphs’, Random Structures Algorithms 7 (1995), 269–271.Google Scholar
Wei, V. K., ‘A lower bound on the stability number of a simple graph’, Bell Laboratories Technical Memorandum 81-11217-9, 1981.Google Scholar