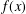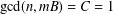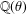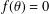Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jones, Lenny
2021.
MONOGENICALLY STABLE POLYNOMIALS.
Albanian Journal of Mathematics,
Vol. 15,
Issue. 2,
Jones, Lenny
2021.
Infinite families of non-monogenic trinomials.
Acta Scientiarum Mathematicarum,
Vol. 87,
Issue. 1-2,
p.
95.
Harrington, Joshua
and
Jones, Lenny
2021.
Some new polynomial discriminant formulas.
Lithuanian Mathematical Journal,
Vol. 61,
Issue. 4,
p.
483.
Jones, Lenny
2022.
On necessary and sufficient conditions for the monogeneity of a certain class of polynomials.
Mathematica Slovaca,
Vol. 72,
Issue. 3,
p.
591.
Gajdzica, Krystian
2022.
Discriminants of special quadrinomials.
Rocky Mountain Journal of Mathematics,
Vol. 52,
Issue. 5,
KAUR, SUMANDEEP
and
KUMAR, SURENDER
2024.
ON A CONJECTURE OF LENNY JONES ABOUT CERTAIN MONOGENIC POLYNOMIALS.
Bulletin of the Australian Mathematical Society,
Vol. 110,
Issue. 1,
p.
72.
Gaál, István
2024.
Monogenity and Power Integral Bases: Recent Developments.
Axioms,
Vol. 13,
Issue. 7,
p.
429.
Jakhar, Anuj
Kalwaniya, Ravi
and
Yadav, Prabhakar
2024.
On the monogenity and Galois group of certain classes of polynomials.
Mathematica Slovaca,
Vol. 74,
Issue. 5,
p.
1147.
Dietmann, Rainer
Ostafe, Alina
and
Shparlinski, Igor E.
2024.
Discriminants of fields generated by polynomials of given height.
Israel Journal of Mathematics,
Vol. 260,
Issue. 1,
p.
73.
JAKHAR, ANUJ
2024.
CHARACTERISATION OF PRIMES DIVIDING THE INDEX OF A CLASS OF POLYNOMIALS AND ITS APPLICATIONS.
Bulletin of the Australian Mathematical Society,
Vol. 110,
Issue. 3,
p.
460.
Jakhar, Anuj
Laishram, Shanta
and
Yadav, Prabhakar
2025.
Explicit discriminant of a class of polynomial, monogenity and Galois group.
Communications in Algebra,
Vol. 53,
Issue. 7,
p.
2937.
Jakhar, Anuj
Kotyada, Srinivas
and
Mukhopadhyay, Arunabha
2025.
Monogenic polynomials and symmetric Galois groups: a quantitative study.
The Ramanujan Journal,
Vol. 67,
Issue. 3,
Kaur, Sumandeep
Kumar, Surender
and
Remete, László
2025.
On the index of power compositional polynomials.
Finite Fields and Their Applications,
Vol. 107,
Issue. ,
p.
102642.
Jakhar, Anuj
Kalwaniya, Ravi
and
Kotyada, Srinivas
2025.
On monogenity of number fields and Galois group.
International Journal of Number Theory,
Vol. 21,
Issue. 08,
p.
1995.
KUMAR, SURENDER
2025.
MONOGENITY OF THE COMPOSITION OF POLYNOMIALS.
Bulletin of the Australian Mathematical Society,
p.
1.