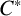 $C^*$-ALGEBRAS OF SELF-SIMILAR ACTION OF GROUPOIDS ON ROW-FINITE DIRECTED GRAPHS
$C^*$-ALGEBRAS OF SELF-SIMILAR ACTION OF GROUPOIDS ON ROW-FINITE DIRECTED GRAPHSPublished online by Cambridge University Press: 08 November 2022
For amenable discrete groupoids 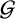 $\mathcal {G}$ and row-finite directed graphs E, let
$\mathcal {G}$ and row-finite directed graphs E, let 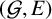 $(\mathcal {G},E)$ be a self-similar groupoid and let
$(\mathcal {G},E)$ be a self-similar groupoid and let 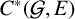 $C^*(\mathcal {G}, E)$ be the associated
$C^*(\mathcal {G}, E)$ be the associated 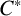 $C^*$-algebra. We introduce a weaker faithfulness condition than those in the existing literature that still guarantees that
$C^*$-algebra. We introduce a weaker faithfulness condition than those in the existing literature that still guarantees that 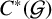 $C^*(\mathcal {G})$ embeds in
$C^*(\mathcal {G})$ embeds in 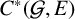 $C^*(\mathcal {G}, E)$. Under this faithfulness condition, we prove a gauge-invariant uniqueness theorem.
$C^*(\mathcal {G}, E)$. Under this faithfulness condition, we prove a gauge-invariant uniqueness theorem.
This work is supported by a PhD scholarship of The Ministry of Education, Culture, Research and Technology of the Republic of Indonesia.