No CrossRef data available.
Article contents
CENTRAL SEQUENCES IN SUBHOMOGENEOUS UNITAL C*-ALGEBRAS
Part of:
Selfadjoint operator algebras
Published online by Cambridge University Press: 02 October 2020
Abstract
Suppose that
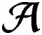 $\mathcal {A}$
is a unital subhomogeneous C*-algebra. We show that every central sequence in
$\mathcal {A}$
is a unital subhomogeneous C*-algebra. We show that every central sequence in
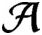 $\mathcal {A}$
is hypercentral if and only if every pointwise limit of a sequence of irreducible representations is multiplicity free. We also show that every central sequence in
$\mathcal {A}$
is hypercentral if and only if every pointwise limit of a sequence of irreducible representations is multiplicity free. We also show that every central sequence in
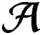 $\mathcal {A}$
is trivial if and only if every pointwise limit of irreducible representations is irreducible. Finally, we give a nice representation of the latter algebras.
$\mathcal {A}$
is trivial if and only if every pointwise limit of irreducible representations is irreducible. Finally, we give a nice representation of the latter algebras.
MSC classification
Primary:
46L40: Automorphisms
- Type
- Research Article
- Information
- Copyright
- © 2020 Australian Mathematical Publishing Association Inc.
References
Akemann, C. A. and Pedersen, G. K., ‘Central sequences and inner derivations of separable C*-algebras’, Amer. J. Math. 101(5) (1979), 1047–1061.CrossRefGoogle Scholar
Ando, H. and Kirchberg, E., ‘Non-commutativity of the central sequence algebra for separable non-type I C*-algebras’, J. Lond. Math. Soc. (2) 94(1) (2016), 280–294.CrossRefGoogle Scholar
Glimm, J., ‘A Stone–Weierstrass theorem for C*-algebras’, Ann. of Math. (2) 72 (1960), 216–244.CrossRefGoogle Scholar
McDuff, D., ‘Central sequences and the hyperfinite factor’, Proc. Lond. Math. Soc. (3) 21 (1970), 443–461.CrossRefGoogle Scholar
Pendharkar, H., Central Sequences and C*-Algebras, PhD Dissertation, University of New Hampshire, 1999.Google Scholar
Phillips, J., ‘Central sequences and automorphisms of C*-algebras’, Amer. J. Math. 110(6) (1988), 1095–1117.CrossRefGoogle Scholar
Robert, L., ‘Is there an upper bound on the dimension for irreducible representations of a continuous trace C*-algebra?’ Mathoverflow, https://mathoverflow.net/q/110582 (version: 2012-10-26).Google Scholar



