Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-24T20:48:23.511Z Has data issue: false hasContentIssue false
  • English
  • Français

CHARACTER CLUSTERS FOR LIE ALGEBRA MODULES OVER A FIELD OF NONZERO CHARACTERISTIC

Part of: Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  07 June 2013

DONALD W. BARNES
DONALD W. BARNES*
Affiliation:
Little Wonga Road, Cremorne, NSW 2090, Australia email donwb@iprimus.com.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a Lie algebra 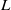$L$ over an algebraically closed field 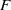$F$ of nonzero characteristic, every finite dimensional 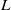$L$-module can be decomposed into a direct sum of submodules such that all composition factors of a summand have the same character. Using the concept of a character cluster, this result is generalised to fields which are not algebraically closed. Also, it is shown that if the soluble Lie algebra 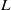$L$ is in the saturated formation 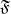$\mathfrak{F}$ and if 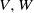$V, W$ are irreducible 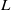$L$-modules with the same cluster and the 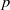$p$-operation vanishes on the centre of the 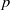$p$-envelope used, then 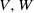$V, W$ are either both 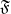$\mathfrak{F}$-central or both 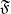$\mathfrak{F}$-eccentric. Clusters are used to generalise the construction of induced modules.

Keywords

Lie algebrassaturated formationsinduced modules

MSC classification

Secondary: 17B10: Representations, algebraic theory (weights)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 89 , Issue 2 , April 2014 , pp. 234 - 242
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Barnes, D. W., ‘On $\mathfrak{F}$-hyperexcentric modules for Lie algebras’, J. Aust. Math. Soc. 74 (2003), 235–238.CrossRefGoogle Scholar
Barnes, D. W., ‘Ado-Iwasawa extras’, J. Aust. Math. Soc. 78 (2005), 407–421.Google Scholar
Barnes, D. W., ‘On locally defined formations of soluble Lie and Leibnitz algebras’, Bull. Aust. Math. Soc. 86 (2012), 322–326.Google Scholar
Kelarev, A. V., ‘Directed graphs and Lie superalgebras of matrices’, J. Algebra 285 (2005), 1–10.Google Scholar
Rakhimov, I. S. and Hassan, M. A., ‘On one-dimensional Leibnitz central extensions of a filiform Lie algebra’, Bull. Aust. Math. Soc. 84 (2011), 205–224.Google Scholar
Shahryari, M., ‘A note on derivations of Lie algebras’, Bull. Aust. Math. Soc. 84 (2011), 444–446.Google Scholar
Strade, H. and Farnsteiner, R., Modular Lie Algebras and their Representations (Marcel Dekker, Inc., New York, Basel, 1988).Google Scholar