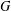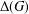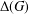Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ebrahimi, Mahdi
2022.
n-Exact character graphs.
Communications in Algebra,
Vol. 50,
Issue. 7,
p.
3149.