Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-10T15:43:01.104Z Has data issue: false hasContentIssue false
  • English
  • Français

A CHARACTERISATION OF CENTRAL ELEMENTS IN 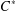$C^{\ast }$ -ALGEBRAS

Part of: Selfadjoint operator algebras Special classes of linear operators

Published online by Cambridge University Press:  19 October 2016

LAJOS MOLNÁR
LAJOS MOLNÁR*
Affiliation:
Department of Analysis, Bolyai Institute, University of Szeged, H-6720 Szeged, Aradi vértanúk tere 1, Hungary MTA-DE ‘Lendület’ Functional Analysis Research Group, Institute of Mathematics, University of Debrecen, H-4010 Debrecen, PO Box 12, Hungary email molnarl@math.u-szeged.hu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Wu [‘An order characterization of commutativity for 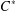$C^{\ast }$ -algebras’, Proc. Amer. Math. Soc.129 (2001), 983–987] proved that if the exponential function on the set of all positive elements of a 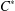$C^{\ast }$ -algebra is monotone in the usual partial order, then the algebra in question is necessarily commutative. In this note, we present a local version of that result and obtain a characterisation of central elements in 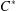$C^{\ast }$ -algebras in terms of the order.

Keywords

C ∗ -algebracentral elementorderexponential function

MSC classification

Primary: 46L05: General theory of $C^*$-algebras
Secondary: 47B49: Transformers, preservers (operators on spaces of operators)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 95 , Issue 1 , February 2017 , pp. 138 - 143
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Fukamiya, M., Misonou, Y. and Takeda, Z., ‘On order and commutativity of B ∗ -algebras’, Tôhoku Math. J. (2) 6 (1954), 89–93.CrossRefGoogle Scholar
Kadison, R. V. and Ringrose, J. R., Fundamentals of the Theory of Operator Algebras, Vol. I (Academic Press, New York, 1983).Google Scholar
Kadison, R. V. and Ringrose, J. R., Fundamentals of the Theory of Operator Algebras, Vol. II (Academic Press, New York, 1986).Google Scholar
Ogasawara, T., ‘A theorem on operator algebras’, J. Sci. Hiroshima Univ. Ser. A. 18 (1955), 307–309.Google Scholar
Pedersen, G. K., C ∗ -Algebras and Their Automorphism Groups, London Mathematical Society Monographs, 14 (Academic Press, London, New York, 1979).Google Scholar
Pedersen, G. K., ‘Operator differentiable functions’, Publ. Res. Inst. Math. Sci. 36 (2000), 139–157.CrossRefGoogle Scholar
Sherman, S., ‘Order in operator algebras’, Amer. J. Math. 73 (1951), 227–232.Google Scholar
Wu, W., ‘An order characterization of commutativity for C ∗ -algebras’, Proc. Amer. Math. Soc. 129 (2001), 983–987.Google Scholar