Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-10T15:40:26.091Z Has data issue: false hasContentIssue false
  • English
  • Français

CHARACTERISATIONS OF PARTITION OF UNITIES GENERATED BY ENTIRE FUNCTIONS IN 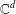$\mathbb{C}^{d}$

Part of: Harmonic analysis in several variables Nontrigonometric harmonic analysis

Published online by Cambridge University Press:  05 January 2017

OLE CHRISTENSEN ,
HONG OH KIM  and
RAE YOUNG KIM
OLE CHRISTENSEN
Affiliation:
Department of Applied Mathematics and Computer Science, Technical University of Denmark, Building 303, 2800 Lyngby, Denmark email ochr@dtu.dk
HONG OH KIM
Affiliation:
Department of Mathematical Sciences, UNIST, 50 UNIST-gil, Ulsan, 44919, Republic of Korea email hkim2031@unist.ac.kr
RAE YOUNG KIM*
Affiliation:
Department of Mathematics, Yeungnam University, 280 Daehak-Ro, Gyeongsan, Gyeongbuk, 38541, Republic of Korea email rykim@ynu.ac.kr
*
✉rykim@ynu.ac.kr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Collections of functions forming a partition of unity play an important role in analysis. In this paper we characterise for any 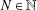$N\in \mathbb{N}$ the entire functions 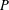$P$ for which the partition of unity condition 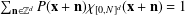$\sum _{\mathbf{n}\in \mathbb{Z}^{d}}P(\mathbf{x}+\mathbf{n})\unicode[STIX]{x1D712}_{[0,N]^{d}}(\mathbf{x}+\mathbf{n})=1$ holds for all 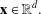$\mathbf{x}\in \mathbb{R}^{d}.$ The general characterisation leads to various easy ways of constructing such entire functions as well. We demonstrate the flexibility of the approach by showing that additional properties like continuity or differentiability of the functions 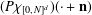$(P\unicode[STIX]{x1D712}_{[0,N]^{d}})(\cdot +\mathbf{n})$ can be controlled. In particular, this leads to easy ways of constructing entire functions 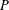$P$ such that the functions in the partition of unity belong to the Feichtinger algebra.

Keywords

entire functionspartition of unityFeichtinger algebra

MSC classification

Primary: 42C40: Wavelets and other special systems
Secondary: 42B05: Fourier series and coefficients
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 95 , Issue 2 , April 2017 , pp. 281 - 290
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

This work was supported by the 2016 Yeungnam University Research Grant and by the National Institute for Mathematical Sciences (NIMS) (A23100000).

References

Christensen, O., Kim, H. O. and Kim, R. Y., ‘On entire functions restricted to intervals, partition of unities, and dual Gabor frames’, Appl. Comput. Harmon. Anal. 38 (2015), 72–86.CrossRefGoogle Scholar
Christensen, O., Kim, H. O. and Kim, R. Y., ‘On partition of unities generated by entire functions and Gabor frames in L 2(ℝ d ) and ℓ 2(ℤ d )’, J. Fourier Anal. Appl. 22 (2016), 1121–1140.Google Scholar
Feichtinger, H. G., ‘On a new Segal algebra’, Monatsh. Math. 92 (1981), 269–289.CrossRefGoogle Scholar
Feichtinger, H. G., ‘Atomic characterizations of modulation spaces through Gabor-type representations’, Rocky Mountain J. Math. 19 (1989), 113–125.Google Scholar
Jakobsen, M. S., ‘On a (no longer new) Segal algebra’, Preprint, 2016.Google Scholar
Janssen, A. J. E. M., ‘The duality condition for Weyl–Heisenberg frames’, in: Gabor Analysis: Theory and Applications (eds. Feichtinger, H. G. and Strohmer, T.) (Birkhäuser, Boston, 1998), 33–84.Google Scholar
Ron, A. and Shen, Z., ‘Frames and stable bases for shift-invariant subspaces of L 2(ℝ d )’, Canad. J. Math. 47(5) (1995), 1051–1094.Google Scholar
Rudin, W., Real and Complex Analysis (McGraw-Hill, New York, 1986).Google Scholar