Hostname: page-component-6bf8c574d5-b4m5d Total loading time: 0 Render date: 2025-02-26T14:52:51.207Z Has data issue: false hasContentIssue false
  • English
  • Français

CLOSURE OPERATORS, FRAMES AND NEATEST REPRESENTATIONS

Part of: Algebraic logic Ordered sets

Published online by Cambridge University Press:  21 June 2017

ROB EGROT Open the ORCID record for ROB EGROT [Opens in a new window]
ROB EGROT*
Affiliation:
Faculty of Information and Communication Technology, Mahidol University, 999 Phuttamonthon 4 Road, Salaya, Nakhon Pathom 73170, Thailand email robert.egr@mahidol.ac.th
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a poset 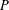$P$ and a standard closure operator 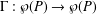$\unicode[STIX]{x1D6E4}:{\wp}(P)\rightarrow {\wp}(P)$, we give a necessary and sufficient condition for the lattice of 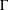$\unicode[STIX]{x1D6E4}$-closed sets of 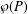${\wp}(P)$ to be a frame in terms of the recursive construction of the 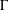$\unicode[STIX]{x1D6E4}$-closure of sets. We use this condition to show that, given a set 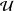${\mathcal{U}}$ of distinguished joins from 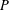$P$, the lattice of 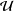${\mathcal{U}}$-ideals of 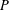$P$ fails to be a frame if and only if it fails to be 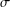$\unicode[STIX]{x1D70E}$-distributive, with 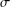$\unicode[STIX]{x1D70E}$ depending on the cardinalities of sets in 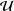${\mathcal{U}}$. From this we deduce that if a poset has the property that whenever 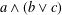$a\wedge (b\vee c)$ is defined for 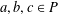$a,b,c\in P$ it is necessarily equal to 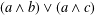$(a\wedge b)\vee (a\wedge c)$, then it has an 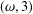$(\unicode[STIX]{x1D714},3)$-representation.

Keywords

posetsclosure operatorsrepresentations

MSC classification

Primary: 06A15: Galois correspondences, closure operators
Secondary: 03G10: Lattices and related structures
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 3 , December 2017 , pp. 361 - 373
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Abian, A., ‘Boolean rings with isomorphisms preserving suprema and infima’, J. Lond. Math. Soc. (2) 3 (1971), 618–620.CrossRefGoogle Scholar
Balbes, R., ‘A representation theory for prime and implicative semilattices’, Trans. Amer. Math. Soc. 136 (1969), 261–267.CrossRefGoogle Scholar
Cheng, Y. and Kemp, P., ‘Representation of posets’, Zeitschr. f. math. Logik und Grundlagen d. Math 38 (1992), 269–276.CrossRefGoogle Scholar
Cornish, W. and Hickman, R., ‘Weakly distributive semilattices’, Acta Math. Acad. Sci. Hungar. 32 (1978), 5–16.CrossRefGoogle Scholar
Doctor, H. P., ‘Extensions of a partially ordered set’, PhD Thesis, McMaster University (Canada), 1967.Google Scholar
Egrot, R., ‘No finite axiomatizations for posets embeddable into distributive lattices’, Preprint, 2016, arXiv:1610.00858.Google Scholar
Egrot, R., ‘Representable posets’, J. Appl. Log. 16 (2016), 60–71.CrossRefGoogle Scholar
Erné, M., ‘Closure’, in: Beyond Topology, Contemporary Mathematics, 486 (Amer. Math. Soc., Providence, RI, 2009), 163–238.CrossRefGoogle Scholar
Erné, M. and Wilke, G., ‘Standard completions for quasiordered sets’, Semigroup Forum 27(1–4) (1983), 351–376.CrossRefGoogle Scholar
Grätzer, G. and Schmidt, E. T., ‘On congruence lattices of lattices’, Acta Math. Acad. Sci. Hungar. 13 (1962), 179–185.CrossRefGoogle Scholar
Hickman, R., ‘Distributivity in semilattices’, Acta Math. Acad. Sci. Hungar. 32 (1978), 35–45.CrossRefGoogle Scholar
Hickman, R. C. and Monro, G. P., ‘Distributive partially ordered sets’, Fund. Math. 120 (1984), 151–166.CrossRefGoogle Scholar
Kearnes, K., ‘The class of prime semilattices is not finitely axiomatizable’, Semigroup Forum 55 (1997), 133–134.CrossRefGoogle Scholar
Kemp, P., ‘Representation of partially ordered sets’, Algebra Universalis 30 (1993), 348–351.CrossRefGoogle Scholar
Schein, B., ‘On the definition of distributive semilattices’, Algebra Universalis 2 (1972), 1–2.CrossRefGoogle Scholar
Schmidt, J., ‘Universal and internal properties of some completions of k-join-semilattices and k-join-distributive partially ordered sets’, J. reine angew. Math. 255 (1972), 8–22.Google Scholar
Schmidt, J., ‘Each join-completion of a partially ordered set is the solution of a universal problem’, J. Aust. Math. Soc. 17 (1974), 406–413.CrossRefGoogle Scholar
Schmidt, J., ‘Universal and internal properties of some extensions of partially ordered sets’, J. reine angew. Math. 253 (1972), 28–42.Google Scholar
Van Alten, C., ‘Embedding ordered sets into distributive lattices’, Order 33 (2016), 419–427.CrossRefGoogle Scholar
Varlet, J. C., ‘On separation properties in semilattices’, Semigroup Forum 10 (1975), 220–228.CrossRefGoogle Scholar