Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-10T19:49:57.670Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPACTNESS OF SPACES OF CONVEX AND SIMPLE QUADRILATERALS

Part of: Topological manifolds General convexity

Published online by Cambridge University Press:  09 September 2016

AHTZIRI GONZÁLEZ  and
JORGE L. LÓPEZ-LÓPEZ
AHTZIRI GONZÁLEZ
Affiliation:
Facultad de Ciencias Físico-Matemáticas, Universidad Michoacana de San Nicolás de Hidalgo, Edificio Alfa, Ciudad Universitaria, C.P. 58040, Morelia, Michoacán, México email ahtziri@cimat.mx
JORGE L. LÓPEZ-LÓPEZ*
Affiliation:
Facultad de Ciencias Físico-Matemáticas, Universidad Michoacana de San Nicolás de Hidalgo, Edificio Alfa, Ciudad Universitaria, C.P. 58040, Morelia, Michoacán, México email jllopez@umich.mx
*
✉jllopez@umich.mx
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The space of shapes of quadrilaterals can be identified with 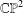$\mathbb{CP}^{2}$. We deal with the subset of 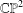$\mathbb{CP}^{2}$ corresponding to convex quadrilaterals and the subset which corresponds to simple (that is, without self-intersections) quadrilaterals. We provide a complete description of the topological closures in 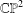$\mathbb{CP}^{2}$ of both spaces. Although the interior of each space is homeomorphic to a disjoint union 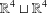$\mathbb{R}^{4}\sqcup \mathbb{R}^{4}$, their closures are topologically different. In particular, the boundary of the space corresponding to convex quadrilaterals is homeomorphic to a pair of three-dimensional spheres glued along a Möbius strip while the boundary of the space corresponding to simple quadrilaterals is more complicated.

Keywords

similarity classshapequadrilateralcompactification

MSC classification

Primary: 57N25: Shapes
Secondary: 57N13: Topology of $E^4$, $4$-manifolds 52A10: Convex sets in $2$ dimensions (including convex curves)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 3 , December 2016 , pp. 507 - 521
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Bavard, C. and Ghys, E., ‘Polygones du plan et polyèdres hyperboliques’, Geom. Dedicata 43(2) (1992), 207–224.CrossRefGoogle Scholar
Freedman, M. H., ‘The topology of four-dimensional manifolds’, J. Differential Geom. 17(3) (1982), 357–453.CrossRefGoogle Scholar
González, A., Topological Properties of the Spaces of Simple and Convex Polygons up to Orientation-Preserving Similarities (in spanish), PhD Thesis, CIMAT, August 2014.Google Scholar
Hatcher, A., Algebraic Topology (Cambridge University Press, Cambridge, 2002).Google Scholar
Kapovich, M. and Millson, J., ‘On the moduli space of polygons in the Euclidean plane’, J. Differential Geom. 42(1) (1995), 133–164.Google Scholar
Kojima, S. and Yamashita, Y., ‘Shapes of stars’, Proc. Amer. Math. Soc. 117(3) (1993), 845–851.Google Scholar
Randrup, T. and Røgen, P., ‘How to twist a knot’, Arch. Math. (Basel) 68 (1997), 252–264.CrossRefGoogle Scholar
Stein, E. M. and Shakarchi, R., Complex Analysis, Princeton Lectures in Analysis II (Princeton University Press, Princeton, 2003).Google Scholar
Thurston, W., ‘Shapes of polyhedra and triangulations of the sphere’, in: The Epstein Birthday Schrift, Geometry & Topology Monographs, vol. 1 (University of Warwick, UK, 1998), 511–549.Google Scholar
Zorich, V. A., Mathematical Analysis II (Universitext, Springer, 2004).Google Scholar