No CrossRef data available.
Article contents
CONGRUENCE OF SYMMETRIC INNER PRODUCTS OVER FINITE COMMUTATIVE RINGS OF ODD CHARACTERISTIC
Published online by Cambridge University Press: 08 June 2017
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let 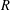 $R$ be a finite commutative ring of odd characteristic and let
$R$ be a finite commutative ring of odd characteristic and let 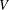 $V$ be a free
$V$ be a free 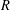 $R$-module of finite rank. We classify symmetric inner products defined on
$R$-module of finite rank. We classify symmetric inner products defined on 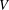 $V$ up to congruence and find the number of such symmetric inner products. Additionally, if
$V$ up to congruence and find the number of such symmetric inner products. Additionally, if 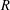 $R$ is a finite local ring, the number of congruent symmetric inner products defined on
$R$ is a finite local ring, the number of congruent symmetric inner products defined on 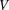 $V$ in each congruence class is determined.
$V$ in each congruence class is determined.
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 96 , Issue 3 , December 2017 , pp. 389 - 397
- Copyright
- © 2017 Australian Mathematical Publishing Association Inc.
References
Bini, G. and Flamini, F., Finite Commutative Rings and Their Applications (Spinger, New York, 2002).CrossRefGoogle Scholar
Casselman, W., ‘Quadratic forms over finite fields’, 2011,http://www.math.ubc.ca/ cass/siegel/Minkowski.pdf.Google Scholar
MacWilliams, J., ‘Orthogonal matrices over finite fields’, Amer. Math. Monthly
76(2) (1969), 152–164.CrossRefGoogle Scholar
McDonald, B. R. and Hershberger, B., ‘The orthogonal group over a full ring’, J. Algebra.
51 (1978), 536–549.CrossRefGoogle Scholar


