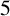1 Introduction
A partition of a positive integer n is a sequence of nonincreasing positive integers whose sum equals n. Let
![]() $p(n)$
denote the number of partitions of n. Ramanujan found and proved the three famous congruences:
$p(n)$
denote the number of partitions of n. Ramanujan found and proved the three famous congruences:
Dyson [Reference Dyson9] defined the rank of a partition to be the largest part minus the number of parts and conjectured that ranks of partitions provided combinatorial interpretations to Ramanujan’s congruences (1.1) and (1.2). Atkin and Swinnerton-Dyer [Reference Atkin and Swinnerton-Dyer3] proved these conjectures. Namely,
where
![]() $N(m,k,n)$
denotes the number of partitions of n with rank congruent to m modulo k. They also obtained the generating functions for every rank difference
$N(m,k,n)$
denotes the number of partitions of n with rank congruent to m modulo k. They also obtained the generating functions for every rank difference
![]() $N(b,\ell ,\ell n+d)-N(c,\ell ,\ell n+d)$
with
$N(b,\ell ,\ell n+d)-N(c,\ell ,\ell n+d)$
with
![]() $\ell =5, 7$
and
$\ell =5, 7$
and
![]() $0\leq b,c,d\leq \ell $
.
$0\leq b,c,d\leq \ell $
.
Inspired by the works of Atkin and Swinnerton-Dyer, many authors studied properties of ranks of partitions. For equalities between
![]() $N(t,k,n)$
and
$N(t,k,n)$
and
![]() $N(s,k,n)$
, see [Reference Andrews, Berndt, Chan, Kim and Malik1, Reference Fan, Xia and Zhao10, Reference Lewis12, Reference Santa-Gadea17]. For example, Andrews et. al. [Reference Andrews, Berndt, Chan, Kim and Malik1] found that
$N(s,k,n)$
, see [Reference Andrews, Berndt, Chan, Kim and Malik1, Reference Fan, Xia and Zhao10, Reference Lewis12, Reference Santa-Gadea17]. For example, Andrews et. al. [Reference Andrews, Berndt, Chan, Kim and Malik1] found that
 $$ \begin{align*} \begin{aligned} N(0,4; 2 n)-N(2,4; 2 n) & = (-1)^n(N(0,8; 2 n)-N(4,8; 2 n)), \\ N(0,4; 2 n+1)-N(2,4; 2 n+1) & = (-1)^n(N(0,8; 2 n+1)+N(1,8; 2 n+1) \\ &\quad -2 N(3,8; 2 n+1)-N(4,8; 2 n+1)). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} N(0,4; 2 n)-N(2,4; 2 n) & = (-1)^n(N(0,8; 2 n)-N(4,8; 2 n)), \\ N(0,4; 2 n+1)-N(2,4; 2 n+1) & = (-1)^n(N(0,8; 2 n+1)+N(1,8; 2 n+1) \\ &\quad -2 N(3,8; 2 n+1)-N(4,8; 2 n+1)). \end{aligned} \end{align*} $$
In [Reference Andrews and Lewis2], Andrews and Lewis made conjectures on inequalities between ranks of partitions modulo
![]() $3$
. Bringmann [Reference Bringmann4] first proved these conjectures: for
$3$
. Bringmann [Reference Bringmann4] first proved these conjectures: for
![]() $n \geq 0$
,
$n \geq 0$
,
 $$ \begin{align} N(0,3,3 n) & < N(1,3,3 n) \quad(n \neq 1,3,7), \\N(0,3,3 n+1) &> N(1,3,3 n+1),\nonumber \\N(0,3,3 n+2) &< N(1,3,3 n+2) .\nonumber \end{align} $$
$$ \begin{align} N(0,3,3 n) & < N(1,3,3 n) \quad(n \neq 1,3,7), \\N(0,3,3 n+1) &> N(1,3,3 n+1),\nonumber \\N(0,3,3 n+2) &< N(1,3,3 n+2) .\nonumber \end{align} $$
When
![]() $n=1,3,7$
, we have equality in (1.4). Bringmann’s proof relies on the circle method to obtain asymptotic results on ranks of partitions modulo
$n=1,3,7$
, we have equality in (1.4). Bringmann’s proof relies on the circle method to obtain asymptotic results on ranks of partitions modulo
![]() $3$
. For more studies on the asymptotic behaviour of ranks of partitions, see [Reference Bringmann and Kane5, Reference Bringmann and Mahlburg6]. Later, Chan and the author provided refinements of these inequalities by using elementary q-series manipulation (see [Reference Chan and Mao7, Corollary 1.7]).
$3$
. For more studies on the asymptotic behaviour of ranks of partitions, see [Reference Bringmann and Kane5, Reference Bringmann and Mahlburg6]. Later, Chan and the author provided refinements of these inequalities by using elementary q-series manipulation (see [Reference Chan and Mao7, Corollary 1.7]).
More recently, Chen et al. [Reference Chen, Chen and Garvan8] studied congruences for ranks of partitions. Let
They proved that, for all
![]() $\alpha \geq 3$
and all
$\alpha \geq 3$
and all
![]() $n \geq 0$
,
$n \geq 0$
,
where
![]() $\delta _\alpha $
satisfies
$\delta _\alpha $
satisfies
![]() $0<\delta _\alpha <5^\alpha $
and
$0<\delta _\alpha <5^\alpha $
and
![]() $24 \delta _\alpha \equiv 1\ (\bmod\ 5^\alpha )$
. In this paper, we establish the following congruences.
$24 \delta _\alpha \equiv 1\ (\bmod\ 5^\alpha )$
. In this paper, we establish the following congruences.
Theorem 1.1. For integers
![]() $\alpha \geq 0$
, let
$\alpha \geq 0$
, let
 $$ \begin{align*} \lambda_{ \alpha} := \left\{\!\! \begin{array}{ll} \dfrac{23\cdot 5^{\alpha}-19}{24}&\textrm{ if } \alpha \text{ is odd,} \\[8pt] \dfrac{19\cdot(5^{\alpha}-1)}{24}&\textrm{ if } \alpha \text{ is even.} \end{array} \right.\!\! \end{align*} $$
$$ \begin{align*} \lambda_{ \alpha} := \left\{\!\! \begin{array}{ll} \dfrac{23\cdot 5^{\alpha}-19}{24}&\textrm{ if } \alpha \text{ is odd,} \\[8pt] \dfrac{19\cdot(5^{\alpha}-1)}{24}&\textrm{ if } \alpha \text{ is even.} \end{array} \right.\!\! \end{align*} $$
Then,
Remark 1.2. From the proof of Proposition 3.1,
Thus,
We prove Theorem 1.1 by arguments similar to those in [Reference Mao and Zhou14, Reference Paule and Radu16, Reference Wang and Yang18]. We first establish some identities between modular functions on
![]() $\Gamma _0(10)$
in Section 2. Then we prove Theorem 1.1 in Section 3.
$\Gamma _0(10)$
in Section 2. Then we prove Theorem 1.1 in Section 3.
2 Preliminaries
Recall the Dedekind eta-function given by
In the above equation and for the rest of this article, we use the notation
 $$ \begin{align*} (x)_{\infty}&:=(x; q)_{\infty}:=\prod_{k=0}^{\infty}(1-x q^{k}) , \end{align*} $$
$$ \begin{align*} (x)_{\infty}&:=(x; q)_{\infty}:=\prod_{k=0}^{\infty}(1-x q^{k}) , \end{align*} $$
where
![]() $q=e^{2\pi i\tau }$
with
$q=e^{2\pi i\tau }$
with
![]() $\text {Im}(\tau )>0$
. We also need
$\text {Im}(\tau )>0$
. We also need
 $$ \begin{align*} \rho&:= \rho(\tau):=\frac{\eta^2(2 \tau) \eta^4(5 \tau)}{\eta^4(\tau) \eta^2(10 \tau)},\\ t&:= t(\tau):=\frac{\eta^2(5 \tau) \eta^2(10 \tau)}{\eta^2(\tau) \eta^2(2 \tau)} ,\\ M&:=M(\tau):=\frac{\eta^2(2\tau)}{\eta^2(50\tau)},\\ K&:=K(\tau)=\frac{\eta(25\tau)}{\eta(\tau)}. \end{align*} $$
$$ \begin{align*} \rho&:= \rho(\tau):=\frac{\eta^2(2 \tau) \eta^4(5 \tau)}{\eta^4(\tau) \eta^2(10 \tau)},\\ t&:= t(\tau):=\frac{\eta^2(5 \tau) \eta^2(10 \tau)}{\eta^2(\tau) \eta^2(2 \tau)} ,\\ M&:=M(\tau):=\frac{\eta^2(2\tau)}{\eta^2(50\tau)},\\ K&:=K(\tau)=\frac{\eta(25\tau)}{\eta(\tau)}. \end{align*} $$
By the criteria for the modularity of eta-products [Reference Newman15, Theorem 4.7],
![]() $\rho , t$
are modular functions on
$\rho , t$
are modular functions on
![]() $\Gamma _0(10)$
and
$\Gamma _0(10)$
and
![]() $M, K$
are on
$M, K$
are on
![]() $\Gamma _0(50)$
and
$\Gamma _0(50)$
and
![]() $\Gamma _0(25)$
, respectively.
$\Gamma _0(25)$
, respectively.
For
![]() $g(\tau ):=\sum _{n=-\infty }^{\infty } a_{g}(n) q^{n}$
, the operator
$g(\tau ):=\sum _{n=-\infty }^{\infty } a_{g}(n) q^{n}$
, the operator
![]() $U_{k}$
is defined by
$U_{k}$
is defined by
 $$ \begin{align*} U_{ k}(g)(\tau):=\frac{1}{k}\sum_{\lambda=0}^{k-1}g\bigg(\frac{\tau+\lambda}{k}\bigg). \end{align*} $$
$$ \begin{align*} U_{ k}(g)(\tau):=\frac{1}{k}\sum_{\lambda=0}^{k-1}g\bigg(\frac{\tau+\lambda}{k}\bigg). \end{align*} $$
One can easily verify that
 $$ \begin{align*} U_{k}(f(q^k)g)(\tau)&=f(q) \sum_{n=-\infty}^{\infty} a_{g}(k n) q^{n}. \end{align*} $$
$$ \begin{align*} U_{k}(f(q^k)g)(\tau)&=f(q) \sum_{n=-\infty}^{\infty} a_{g}(k n) q^{n}. \end{align*} $$
We need the following fundamental lemma.
Lemma 2.1 (See [Reference Wang and Yang18, Lemma 2.3]).
Let
 $$ \begin{align*} & a_0(t)=-t, \\ & a_1(t)=-t(2 \cdot 5+5^2 t), \\& a_2(t)=-t(11 \cdot 5+2 \cdot 5^3 t+5^4 t^2), \\ & a_3(t)=-t(28 \cdot 5+11 \cdot 5^3 t+2 \cdot 5^5 t^2+5^6 t^3), \\ & a_4(t)=-t(7 \cdot 5^2+28 \cdot 5^3 t+11 \cdot 5^5 t^2+2 \cdot 5^7 t^3+5^8 t^4). \end{align*} $$
$$ \begin{align*} & a_0(t)=-t, \\ & a_1(t)=-t(2 \cdot 5+5^2 t), \\& a_2(t)=-t(11 \cdot 5+2 \cdot 5^3 t+5^4 t^2), \\ & a_3(t)=-t(28 \cdot 5+11 \cdot 5^3 t+2 \cdot 5^5 t^2+5^6 t^3), \\ & a_4(t)=-t(7 \cdot 5^2+28 \cdot 5^3 t+11 \cdot 5^5 t^2+2 \cdot 5^7 t^3+5^8 t^4). \end{align*} $$
Then, for
![]() $u: \mathbb {H} \rightarrow \mathbb {C}$
and
$u: \mathbb {H} \rightarrow \mathbb {C}$
and
![]() $j \in \mathbb {Z}$
,
$j \in \mathbb {Z}$
,
 $$ \begin{align} U_5(u t^j)=-\sum_{l=0}^4 a_l(t) U_5(u t^{j+l-5}). \end{align} $$
$$ \begin{align} U_5(u t^j)=-\sum_{l=0}^4 a_l(t) U_5(u t^{j+l-5}). \end{align} $$
Lemma 2.2. Let
![]() $U^{(0,j)}(f):=U_5(K\cdot \rho ^j\cdot f), \ U^{(1,j)}(f):=U_5(M\cdot \rho ^j\cdot f)$
. Then we have four groups of identities.
$U^{(0,j)}(f):=U_5(K\cdot \rho ^j\cdot f), \ U^{(1,j)}(f):=U_5(M\cdot \rho ^j\cdot f)$
. Then we have four groups of identities.
 $$ \begin{align*} & \kern-62pt Group\ I\\U^{(0,0)}(1)&=5\rho t\\ U^{(0,0)}(t^{-1})&=\rho\\ U^{(0,0)}(t^{-2})&=1-4\cdot 5t-5^3t^2+\rho(-4+5^2t)\\ U^{(0,0)}(t^{-3})&=-6+7\cdot5^2t+2\cdot5^4t^2+5^5t^3+\rho(5-4\cdot5^2t)\\ U^{(0,0)}(t^{-4})&=13-18\cdot5^2t-2\cdot5^4t^2+2\cdot5^5t^3+5^7t^4\\&\quad+\rho(2\cdot5^2-5^4t-2\cdot5^5t^2-2\cdot5^6t^3).\\[4pt]& \kern-62pt Group\ II\\U^{(0,1)}(1)&=4t-9\cdot5^2t^2-9\cdot5^4 t^3-31\cdot5^5t^4-7\cdot5^7t^5-5^9t^6\\&\quad+\rho(29\cdot5t+57 \cdot5^3t^2+37\cdot 5^5t^3+63\cdot5^6t^4+11\cdot5^8t^5+5^{10}t^6)\\ U^{(0,1)}( t^{-1})&=-5t+\rho(1+5^2t)\\ U^{(0,1)}( t^{-2})&=-4\cdot5 t-5^3t^2+\rho(1+5^2t)\\ U^{(0,1)}( t^{-3})&=1+18\cdot5t+7\cdot5^3t^2+5^5t^3+\rho(-2\cdot5-3\cdot5^2t-5^4t^2)\\ U^{(0,1)}( t^{-4})&=-2\cdot5+7\cdot5^2t+4\cdot5^4t^2+5^6t^3+5^7t^4 +\rho(9\cdot5-2\cdot5^3t-5^6t^3).\\[4pt]& \kern-62pt Group\ III\\U^{(1,0)}(1)&=-1\\ U^{(1,0)}(t^{-1})&=3\cdot5+4\cdot5^2t+\rho (t^{-1}-5^2)\\ U^{(1,0)}(t^{-2})&=-12\cdot 5- 4\cdot5^3t-5^4t^2+\rho(-4t^{-1}+4\cdot5^2)\\ U^{(1,0)}(t^{-3})&=t^{-1}- 5^5t^2-5^6t^3+\rho(2\cdot5^3+5^5t+5^6t^2)\\ U^{(1,0)}(t^{-4})&=-2\cdot5 t^{-1}+54\cdot5^2+18\cdot5^4t+2\cdot5^6t^2-5^8t^4\\&\quad+\rho(18\cdot5t^{-1}-38\cdot5^3-2\cdot5^6t-2\cdot5^7t^2).\\[4pt]& \kern-62pt Group\ IV\\U^{(1,1)}(1)&=-4-5^2t-5^4t^2+\rho(11\cdot5+5^4t+5^5t^2)\\ U^{(1,1)}( t^{-1})&=2\cdot5+4\cdot5^2t+\rho(t^{-1}-4\cdot5) \\ U^{(1,1)}( t^{-2})&=-5^3t- 5^4t^2+5^3\rho t\\ U^{(1,1)}( t^{-3})&=-33\cdot 5-11\cdot5^3t-5^5t^2-5^6t^3 +\rho(-11t^{-1}+11\cdot5^2+5^5t^2)\\ U^{(1,1)}( t^{-4})&= t^{-1}+33\cdot5^2+11\cdot5^4t-5^5t^2-5^7t^3-5^8t^4\\&\quad+\rho(11\cdot5t^{-1}-9\cdot5^3+5^5t+5^6t^2+5^7t^3).\end{align*} $$
$$ \begin{align*} & \kern-62pt Group\ I\\U^{(0,0)}(1)&=5\rho t\\ U^{(0,0)}(t^{-1})&=\rho\\ U^{(0,0)}(t^{-2})&=1-4\cdot 5t-5^3t^2+\rho(-4+5^2t)\\ U^{(0,0)}(t^{-3})&=-6+7\cdot5^2t+2\cdot5^4t^2+5^5t^3+\rho(5-4\cdot5^2t)\\ U^{(0,0)}(t^{-4})&=13-18\cdot5^2t-2\cdot5^4t^2+2\cdot5^5t^3+5^7t^4\\&\quad+\rho(2\cdot5^2-5^4t-2\cdot5^5t^2-2\cdot5^6t^3).\\[4pt]& \kern-62pt Group\ II\\U^{(0,1)}(1)&=4t-9\cdot5^2t^2-9\cdot5^4 t^3-31\cdot5^5t^4-7\cdot5^7t^5-5^9t^6\\&\quad+\rho(29\cdot5t+57 \cdot5^3t^2+37\cdot 5^5t^3+63\cdot5^6t^4+11\cdot5^8t^5+5^{10}t^6)\\ U^{(0,1)}( t^{-1})&=-5t+\rho(1+5^2t)\\ U^{(0,1)}( t^{-2})&=-4\cdot5 t-5^3t^2+\rho(1+5^2t)\\ U^{(0,1)}( t^{-3})&=1+18\cdot5t+7\cdot5^3t^2+5^5t^3+\rho(-2\cdot5-3\cdot5^2t-5^4t^2)\\ U^{(0,1)}( t^{-4})&=-2\cdot5+7\cdot5^2t+4\cdot5^4t^2+5^6t^3+5^7t^4 +\rho(9\cdot5-2\cdot5^3t-5^6t^3).\\[4pt]& \kern-62pt Group\ III\\U^{(1,0)}(1)&=-1\\ U^{(1,0)}(t^{-1})&=3\cdot5+4\cdot5^2t+\rho (t^{-1}-5^2)\\ U^{(1,0)}(t^{-2})&=-12\cdot 5- 4\cdot5^3t-5^4t^2+\rho(-4t^{-1}+4\cdot5^2)\\ U^{(1,0)}(t^{-3})&=t^{-1}- 5^5t^2-5^6t^3+\rho(2\cdot5^3+5^5t+5^6t^2)\\ U^{(1,0)}(t^{-4})&=-2\cdot5 t^{-1}+54\cdot5^2+18\cdot5^4t+2\cdot5^6t^2-5^8t^4\\&\quad+\rho(18\cdot5t^{-1}-38\cdot5^3-2\cdot5^6t-2\cdot5^7t^2).\\[4pt]& \kern-62pt Group\ IV\\U^{(1,1)}(1)&=-4-5^2t-5^4t^2+\rho(11\cdot5+5^4t+5^5t^2)\\ U^{(1,1)}( t^{-1})&=2\cdot5+4\cdot5^2t+\rho(t^{-1}-4\cdot5) \\ U^{(1,1)}( t^{-2})&=-5^3t- 5^4t^2+5^3\rho t\\ U^{(1,1)}( t^{-3})&=-33\cdot 5-11\cdot5^3t-5^5t^2-5^6t^3 +\rho(-11t^{-1}+11\cdot5^2+5^5t^2)\\ U^{(1,1)}( t^{-4})&= t^{-1}+33\cdot5^2+11\cdot5^4t-5^5t^2-5^7t^3-5^8t^4\\&\quad+\rho(11\cdot5t^{-1}-9\cdot5^3+5^5t+5^6t^2+5^7t^3).\end{align*} $$
Sketch of proof.
The equations in Groups I–IV are identities between modular functions on
![]() $\Gamma _0(10)$
. One can automatically prove them by the MAPLE package ETA [Reference Garvan11]. For example, the Maple commands for verifying the second identity in Group II are provided at https://github.com/dongpanghu/code5.
$\Gamma _0(10)$
. One can automatically prove them by the MAPLE package ETA [Reference Garvan11]. For example, the Maple commands for verifying the second identity in Group II are provided at https://github.com/dongpanghu/code5.
We call a map
![]() $d: \mathbb {Z} \times \mathbb {Z} \longrightarrow \mathbb {Z}$
a discrete array if for each i, the map
$d: \mathbb {Z} \times \mathbb {Z} \longrightarrow \mathbb {Z}$
a discrete array if for each i, the map
![]() ${d(i,-): \mathbb {Z} \longrightarrow \mathbb {Z}}$
given by
${d(i,-): \mathbb {Z} \longrightarrow \mathbb {Z}}$
given by
![]() $j \mapsto d(i, j)$
has finite support.
$j \mapsto d(i, j)$
has finite support.
Lemma 2.3. There exist discrete arrays
![]() $a_{i,j}, b_{i,j}$
with
$a_{i,j}, b_{i,j}$
with
![]() $0\leq i, j\leq 1$
such that for
$0\leq i, j\leq 1$
such that for
![]() $k\in \mathbb {Z}$
,
$k\in \mathbb {Z}$
,
 $$ \begin{align} U^{(i,j)}( t^k)= \sum_{n=\lceil{(k-s_{i,j})}/{5}\rceil}^{\infty} a_{i,j}(k, n) t^n+\rho\,\bigg(\sum_{n=\lceil{(k-s_{i,j})}/{5}\rceil}^{\infty} b_{i,j}(k, n) t^n\bigg), \end{align} $$
$$ \begin{align} U^{(i,j)}( t^k)= \sum_{n=\lceil{(k-s_{i,j})}/{5}\rceil}^{\infty} a_{i,j}(k, n) t^n+\rho\,\bigg(\sum_{n=\lceil{(k-s_{i,j})}/{5}\rceil}^{\infty} b_{i,j}(k, n) t^n\bigg), \end{align} $$
where
 $$ \begin{align*} s_{i,j}=\left\{\!\! \begin{array}{cl} -1 & \text{when}\ (i,j)=(0,0),\\ - 1 & \text{when}\ (i,j)=(0,1),\\ 4 & \text{when}\ (i,j)=(1,0),\\ 4 & \text{when}\ (i,j)=(1,1). \end{array} \right.\!\! \end{align*} $$
$$ \begin{align*} s_{i,j}=\left\{\!\! \begin{array}{cl} -1 & \text{when}\ (i,j)=(0,0),\\ - 1 & \text{when}\ (i,j)=(0,1),\\ 4 & \text{when}\ (i,j)=(1,0),\\ 4 & \text{when}\ (i,j)=(1,1). \end{array} \right.\!\! \end{align*} $$
Moreover, the values of
![]() $a_{i,j}(k, n)$
and
$a_{i,j}(k, n)$
and
![]() $b_{i,j}(k, n)$
for
$b_{i,j}(k, n)$
for
![]() $-4 \leq k\leq 0$
are given in Groups I–IV of Lemma 2.2 and, for other
$-4 \leq k\leq 0$
are given in Groups I–IV of Lemma 2.2 and, for other
![]() $k, a_{i,j}(k, n), b_{i,j}(k, n)$
, satisfy the recurrence relation in [Reference Wang and Yang18, (2.17)]:
$k, a_{i,j}(k, n), b_{i,j}(k, n)$
, satisfy the recurrence relation in [Reference Wang and Yang18, (2.17)]:
 $$ \begin{align} m( k, n)&= (7 \cdot 5^2 m( k-1, n-1)+28 \cdot 5^3 m( k-1, n-2)+11 \cdot 5^5 m( k-1, n-3)\nonumber\\ &\quad +2 \cdot 5^7 m( k-1, n-4)+5^8 m( k-1, n-5))+(28 \cdot 5 m( k-2, n-1)\nonumber \\ &\quad +11 \cdot 5^3 m( k-2, n-2)+2 \cdot 5^5 m( k-2, n-3)+5^6 m( k-2, n-4)) \nonumber\\ &\quad +(11 \cdot 5 m( k-3, n-1)+2 \cdot 5^3 m( k-3, n-2)+5^4 m( k-3, n-3)) \nonumber\\ &\quad + (2 \cdot 5 m( k-4, n-1)+5^2 m( k-4, n-2))+m( k-5, n-1). \end{align} $$
$$ \begin{align} m( k, n)&= (7 \cdot 5^2 m( k-1, n-1)+28 \cdot 5^3 m( k-1, n-2)+11 \cdot 5^5 m( k-1, n-3)\nonumber\\ &\quad +2 \cdot 5^7 m( k-1, n-4)+5^8 m( k-1, n-5))+(28 \cdot 5 m( k-2, n-1)\nonumber \\ &\quad +11 \cdot 5^3 m( k-2, n-2)+2 \cdot 5^5 m( k-2, n-3)+5^6 m( k-2, n-4)) \nonumber\\ &\quad +(11 \cdot 5 m( k-3, n-1)+2 \cdot 5^3 m( k-3, n-2)+5^4 m( k-3, n-3)) \nonumber\\ &\quad + (2 \cdot 5 m( k-4, n-1)+5^2 m( k-4, n-2))+m( k-5, n-1). \end{align} $$
Proof. We verify that the result holds for
![]() $-4 \leq k\leq 0$
by Groups I–IV in Lemma 2.2. Then we apply (2.1) to prove Lemma 2.3 by induction on k.
$-4 \leq k\leq 0$
by Groups I–IV in Lemma 2.2. Then we apply (2.1) to prove Lemma 2.3 by induction on k.
Denote the
![]() $5$
-adic order of n by
$5$
-adic order of n by
![]() $\pi (n)$
and set
$\pi (n)$
and set
![]() $\pi (0)=+\infty $
.
$\pi (0)=+\infty $
.
Lemma 2.4 [Reference Wang and Yang18, Lemma 2.8].
Let
![]() $g(k, n)$
be integers which satisfy the recurrence relation (2.3). Suppose there exists an integer l and a constant
$g(k, n)$
be integers which satisfy the recurrence relation (2.3). Suppose there exists an integer l and a constant
![]() $\gamma $
such that, for
$\gamma $
such that, for
![]() $l \leq k \leq l+4$
,
$l \leq k \leq l+4$
,
Then (2.4) holds for any
![]() $k \in \mathbb {Z}$
.
$k \in \mathbb {Z}$
.
Lemma 2.5. Recall that
![]() $a_{i, j}, b_{i, j}$
are given in Lemma 2.3. For
$a_{i, j}, b_{i, j}$
are given in Lemma 2.3. For
![]() $n, k\in \mathbb {Z}$
,
$n, k\in \mathbb {Z}$
,
 $$ \begin{align*} \pi(a_{0,0}(k, n)) \geq\bigg\lfloor\frac{5 n-k-2}{3}\bigg\rfloor , &\quad \pi(b_{0,0}(k, n)) \geq\bigg\lfloor\frac{5 n-k}{3}\bigg\rfloor , \\ \pi(a_{0,1}(k, n)) \geq\bigg\lfloor\frac{5 n-k-3}{3}\bigg\rfloor , &\quad \pi(b_{0,1}(k, n)) \geq\bigg\lfloor\frac{5 n-k}{3}\bigg\rfloor ,\\ \pi(a_{1,0}(k, n)) \geq\bigg\lfloor\frac{5 n-k+2}{3}\bigg\rfloor , &\quad \pi(b_{1,0}(k, n)) \geq\bigg\lfloor\frac{5 n-k+5}{3}\bigg\rfloor ,\\ \pi(a_{1,1}(k, n)) \geq\bigg\lfloor\frac{5 n-k+2}{3}\bigg\rfloor , &\quad \pi(b_{1,1}(k, n)) \geq\bigg\lfloor\frac{5 n-k+4}{3}\bigg\rfloor. \end{align*} $$
$$ \begin{align*} \pi(a_{0,0}(k, n)) \geq\bigg\lfloor\frac{5 n-k-2}{3}\bigg\rfloor , &\quad \pi(b_{0,0}(k, n)) \geq\bigg\lfloor\frac{5 n-k}{3}\bigg\rfloor , \\ \pi(a_{0,1}(k, n)) \geq\bigg\lfloor\frac{5 n-k-3}{3}\bigg\rfloor , &\quad \pi(b_{0,1}(k, n)) \geq\bigg\lfloor\frac{5 n-k}{3}\bigg\rfloor ,\\ \pi(a_{1,0}(k, n)) \geq\bigg\lfloor\frac{5 n-k+2}{3}\bigg\rfloor , &\quad \pi(b_{1,0}(k, n)) \geq\bigg\lfloor\frac{5 n-k+5}{3}\bigg\rfloor ,\\ \pi(a_{1,1}(k, n)) \geq\bigg\lfloor\frac{5 n-k+2}{3}\bigg\rfloor , &\quad \pi(b_{1,1}(k, n)) \geq\bigg\lfloor\frac{5 n-k+4}{3}\bigg\rfloor. \end{align*} $$
3 Proof of Theorem 1.1
We first need the following generating function.
Proposition 3.1. We have
 $$ \begin{align} \sum_{n=0}^{\infty}(N(1,10,5n+4)-N(5,10,5n+4))q^n=\frac{(q^{10}; q^{10})^2_{\infty}} {(q; q)_{\infty}}. \end{align} $$
$$ \begin{align} \sum_{n=0}^{\infty}(N(1,10,5n+4)-N(5,10,5n+4))q^n=\frac{(q^{10}; q^{10})^2_{\infty}} {(q; q)_{\infty}}. \end{align} $$
Proof. We deduce from [Reference Mao13, (1.14)] that
 $$ \begin{align} &\sum_{n=0}^{\infty}(N(0,10,5n+4)+N(1,10,5n+4) -N(4,10,5n+4) -N(5,10,5n+4))q^n\nonumber\\ &\quad =\frac{2(q^{10}; q^{10})^2_{\infty}} {(q; q)_{\infty}}. \end{align} $$
$$ \begin{align} &\sum_{n=0}^{\infty}(N(0,10,5n+4)+N(1,10,5n+4) -N(4,10,5n+4) -N(5,10,5n+4))q^n\nonumber\\ &\quad =\frac{2(q^{10}; q^{10})^2_{\infty}} {(q; q)_{\infty}}. \end{align} $$
Note that
and
which together with (1.3) give
Define
 $$ \begin{align*} \sum_{n=0}^\infty e(n)q^n:=\frac{(q^{10}; q^{10})^2_{\infty}} {(q; q)_{\infty}}. \end{align*} $$
$$ \begin{align*} \sum_{n=0}^\infty e(n)q^n:=\frac{(q^{10}; q^{10})^2_{\infty}} {(q; q)_{\infty}}. \end{align*} $$
Then Proposition 3.1 implies
Let
![]() $ L_0:=1$
and, for
$ L_0:=1$
and, for
![]() $\alpha \geq 1$
,
$\alpha \geq 1$
,
 $$ \begin{align*} L_{2\alpha -1}& :=\frac{(q^{5}; q^{5})_{\infty}}{(q^2; q^2)^2_{\infty}}\sum_{n=0}^\infty e(5^{2\alpha -1}n+\lambda_{2\alpha-1})q^{n+1},\\ L_{2 \alpha} & :=\frac{(q; q)_{\infty}}{(q^{10}; q^{10})^2_{\infty}} \sum_{n=0}^{\infty} e(5^{2 \alpha} n+\lambda_{2 \alpha}) q^{n}. \end{align*} $$
$$ \begin{align*} L_{2\alpha -1}& :=\frac{(q^{5}; q^{5})_{\infty}}{(q^2; q^2)^2_{\infty}}\sum_{n=0}^\infty e(5^{2\alpha -1}n+\lambda_{2\alpha-1})q^{n+1},\\ L_{2 \alpha} & :=\frac{(q; q)_{\infty}}{(q^{10}; q^{10})^2_{\infty}} \sum_{n=0}^{\infty} e(5^{2 \alpha} n+\lambda_{2 \alpha}) q^{n}. \end{align*} $$
Lemma 3.2. For all
![]() $\alpha \geq 0$
,
$\alpha \geq 0$
,
Proof. For any
![]() $\alpha \geq 0$
,
$\alpha \geq 0$
,
 $$ \begin{align*} U^{(0,0)}(L_{2 \alpha})& =U_5\bigg(\frac{q(q^{25}; q^{25})_{\infty}}{(q; q)_{\infty}}\cdot\frac{(q; q)_{\infty}}{(q^{10}; q^{10})^2_{\infty}} \sum_{n=0}^{\infty} e(5^{2 \alpha} n+\lambda_{2 \alpha}) q^{n}\bigg) \\ & =\frac{(q^{5}; q^{5})_{\infty}}{(q^2; q^2)^2_{\infty}} \cdot U_5\bigg(\sum^\infty_{n =0} e(5^{2 \alpha}n+\lambda_{2 \alpha}) q^{n+1}\bigg) \\ & =\frac{(q^{5}; q^{5})_{\infty}}{(q^2; q^2)^2_{\infty}} \cdot \sum^\infty_{n =0} e(5^{2 \alpha}(5n+4)+\lambda_{2 \alpha}) q^{n+1}\\ & =\frac{(q^{5}; q^{5})_{\infty}}{(q^2; q^2)^2_{\infty}} \cdot \sum^\infty_{n =0} e(5^{2 \alpha+1}n+\lambda_{2 \alpha+1}) q^{n+1} \\ &=L_{2\alpha+1}. \end{align*} $$
$$ \begin{align*} U^{(0,0)}(L_{2 \alpha})& =U_5\bigg(\frac{q(q^{25}; q^{25})_{\infty}}{(q; q)_{\infty}}\cdot\frac{(q; q)_{\infty}}{(q^{10}; q^{10})^2_{\infty}} \sum_{n=0}^{\infty} e(5^{2 \alpha} n+\lambda_{2 \alpha}) q^{n}\bigg) \\ & =\frac{(q^{5}; q^{5})_{\infty}}{(q^2; q^2)^2_{\infty}} \cdot U_5\bigg(\sum^\infty_{n =0} e(5^{2 \alpha}n+\lambda_{2 \alpha}) q^{n+1}\bigg) \\ & =\frac{(q^{5}; q^{5})_{\infty}}{(q^2; q^2)^2_{\infty}} \cdot \sum^\infty_{n =0} e(5^{2 \alpha}(5n+4)+\lambda_{2 \alpha}) q^{n+1}\\ & =\frac{(q^{5}; q^{5})_{\infty}}{(q^2; q^2)^2_{\infty}} \cdot \sum^\infty_{n =0} e(5^{2 \alpha+1}n+\lambda_{2 \alpha+1}) q^{n+1} \\ &=L_{2\alpha+1}. \end{align*} $$
Similarly,
 $$ \begin{align*} U^{(1,0)}( L_{2 \alpha+1}) & =U_5\bigg(\frac{(q^2; q^2)^2_{\infty}}{q^4(q^{50}; q^{50})^2_{\infty}}\cdot\frac{(q^{5}; q^{5})_{\infty}}{(q^2; q^2)^2_{\infty}}\sum_{n=0}^\infty e(5^{2\alpha +1}n+\lambda_{2\alpha+1})q^{n+1}\bigg) \\ & =\frac{(q; q)_{\infty}}{(q^{10}; q^{10})^2_{\infty}} \cdot U_5\bigg(\sum^\infty_{n =0} e(5^{2 \alpha+1}n+\lambda_{2 \alpha+1}) q^{n-3}\bigg) \\ & =\frac{(q; q)_{\infty}}{(q^{10}; q^{10})^2_{\infty}} \cdot \sum^\infty_{n =0} e(5^{2 \alpha+1}(5n+3)+\lambda_{2 \alpha+1}) q^{n} \\ & =\frac{(q; q)_{\infty}}{(q^{10}; q^{10})^2_{\infty}} \cdot \sum^\infty_{n =0} e(5^{2 \alpha+2}n+\lambda_{2 \alpha+2}) q^{n} \\ &=L_{2\alpha+2}.\\[-35pt] \end{align*} $$
$$ \begin{align*} U^{(1,0)}( L_{2 \alpha+1}) & =U_5\bigg(\frac{(q^2; q^2)^2_{\infty}}{q^4(q^{50}; q^{50})^2_{\infty}}\cdot\frac{(q^{5}; q^{5})_{\infty}}{(q^2; q^2)^2_{\infty}}\sum_{n=0}^\infty e(5^{2\alpha +1}n+\lambda_{2\alpha+1})q^{n+1}\bigg) \\ & =\frac{(q; q)_{\infty}}{(q^{10}; q^{10})^2_{\infty}} \cdot U_5\bigg(\sum^\infty_{n =0} e(5^{2 \alpha+1}n+\lambda_{2 \alpha+1}) q^{n-3}\bigg) \\ & =\frac{(q; q)_{\infty}}{(q^{10}; q^{10})^2_{\infty}} \cdot \sum^\infty_{n =0} e(5^{2 \alpha+1}(5n+3)+\lambda_{2 \alpha+1}) q^{n} \\ & =\frac{(q; q)_{\infty}}{(q^{10}; q^{10})^2_{\infty}} \cdot \sum^\infty_{n =0} e(5^{2 \alpha+2}n+\lambda_{2 \alpha+2}) q^{n} \\ &=L_{2\alpha+2}.\\[-35pt] \end{align*} $$
Theorem 3.3. There exists discrete arrays
![]() $c, d$
such that for
$c, d$
such that for
![]() $\alpha \geq 1$
,
$\alpha \geq 1$
,
 $$ \begin{align*} L_{\alpha}= \sum_{n\geq\delta_\alpha}c(\alpha,n)t^n+\rho\bigg(\sum_{n\geq\delta_\alpha}d(\alpha,n)t^n\bigg), \end{align*} $$
$$ \begin{align*} L_{\alpha}= \sum_{n\geq\delta_\alpha}c(\alpha,n)t^n+\rho\bigg(\sum_{n\geq\delta_\alpha}d(\alpha,n)t^n\bigg), \end{align*} $$
where
 $$ \begin{align*} \delta_\alpha=\left\{\!\! \begin{array}{ll} 1&\text{if}\ \alpha \text{ is odd},\\ 0&\text{otherwise}. \end{array} \right. \end{align*} $$
$$ \begin{align*} \delta_\alpha=\left\{\!\! \begin{array}{ll} 1&\text{if}\ \alpha \text{ is odd},\\ 0&\text{otherwise}. \end{array} \right. \end{align*} $$
Moreover,
 $$ \begin{align} \pi(c(\alpha,n))\geq\left\{\!\! \begin{array}{ll} \dfrac{\alpha-1}{2}+\bigg\lfloor\dfrac{5 n-2}{3}\bigg\rfloor &\text{if}\ \alpha \text{ is odd},\\[5pt] \dfrac{\alpha}{2}+\bigg\lfloor\dfrac{5 n+1}{3}\bigg\rfloor & \text{otherwise} \end{array} \right. \end{align} $$
$$ \begin{align} \pi(c(\alpha,n))\geq\left\{\!\! \begin{array}{ll} \dfrac{\alpha-1}{2}+\bigg\lfloor\dfrac{5 n-2}{3}\bigg\rfloor &\text{if}\ \alpha \text{ is odd},\\[5pt] \dfrac{\alpha}{2}+\bigg\lfloor\dfrac{5 n+1}{3}\bigg\rfloor & \text{otherwise} \end{array} \right. \end{align} $$
and
 $$ \begin{align} \pi(d(\alpha,n))\geq\left\{\!\! \begin{array}{ll} \dfrac{\alpha-1}{2}+\bigg\lfloor\dfrac{5 n}{3}\bigg\rfloor & \text{if}\ \alpha \text{ is odd,}\\[5pt] \dfrac{\alpha}{2}+\bigg\lfloor\dfrac{5 n+3}{3}\bigg\rfloor & \text{otherwise.} \end{array} \right.\!\! \end{align} $$
$$ \begin{align} \pi(d(\alpha,n))\geq\left\{\!\! \begin{array}{ll} \dfrac{\alpha-1}{2}+\bigg\lfloor\dfrac{5 n}{3}\bigg\rfloor & \text{if}\ \alpha \text{ is odd,}\\[5pt] \dfrac{\alpha}{2}+\bigg\lfloor\dfrac{5 n+3}{3}\bigg\rfloor & \text{otherwise.} \end{array} \right.\!\! \end{align} $$
Proof. Let
![]() $c(1,k)=0$
for
$c(1,k)=0$
for
![]() $k\geq 1$
and
$k\geq 1$
and
![]() $d(1,1)=5, d(1,k)=0$
for
$d(1,1)=5, d(1,k)=0$
for
![]() $k\geq 2$
. For
$k\geq 2$
. For
![]() $\alpha \geq 1$
, define
$\alpha \geq 1$
, define
 $$ \begin{align*} c(2\alpha,n)&=\sum_{k\geq1}[c(2\alpha-1,k)a_{1,0}(k,n)+d(2\alpha-1,k)a_{1,1}(k,n)],\\ d(2\alpha,n)&=\sum_{k\geq1}[c(2\alpha-1,k)b_{1,0}(k,n)+d(2\alpha-1,k)b_{1,1}(k,n)],\\ c(2\alpha+1,n)&=\sum_{k\geq0}[c(2\alpha,k)a_{0,0}(k,n)+d(2\alpha,k)a_{0,1}(k,n)],\\ d(2\alpha+1,n)&=\sum_{k\geq0}[c(2\alpha,k)b_{0,0}(k,n)+d(2\alpha,k)b_{0,1}(k,n)]. \end{align*} $$
$$ \begin{align*} c(2\alpha,n)&=\sum_{k\geq1}[c(2\alpha-1,k)a_{1,0}(k,n)+d(2\alpha-1,k)a_{1,1}(k,n)],\\ d(2\alpha,n)&=\sum_{k\geq1}[c(2\alpha-1,k)b_{1,0}(k,n)+d(2\alpha-1,k)b_{1,1}(k,n)],\\ c(2\alpha+1,n)&=\sum_{k\geq0}[c(2\alpha,k)a_{0,0}(k,n)+d(2\alpha,k)a_{0,1}(k,n)],\\ d(2\alpha+1,n)&=\sum_{k\geq0}[c(2\alpha,k)b_{0,0}(k,n)+d(2\alpha,k)b_{0,1}(k,n)]. \end{align*} $$
From Lemma 2.2, Group I and (3.5),
 $$ \begin{align*} L_1=U^{(0,0)}(L_0)=U^{(0,0)}(1)=\rho\bigg(\sum_{n=1}^1d(1,n)t^n\bigg), \end{align*} $$
$$ \begin{align*} L_1=U^{(0,0)}(L_0)=U^{(0,0)}(1)=\rho\bigg(\sum_{n=1}^1d(1,n)t^n\bigg), \end{align*} $$
which gives
![]() $\pi (c(1,n))\geq \lfloor {(5 n-2)}/{3}\rfloor $
and
$\pi (c(1,n))\geq \lfloor {(5 n-2)}/{3}\rfloor $
and
![]() $\pi (d(1,n))\geq \lfloor {5 n}/{3}\rfloor $
. From (3.6),
$\pi (d(1,n))\geq \lfloor {5 n}/{3}\rfloor $
. From (3.6),
 $$ \begin{align*} L_2&=U^{(1,0)}(L_1)=U_5(M\cdot L_1) \nonumber =\sum_{n=1}^1d(1,n)U_5(M\rho t^n) \nonumber =\sum_{n=1}^1d(1,n)U^{(1,1)}( t^n)\nonumber \\&=\sum_{n=1}^1d(1,n) \bigg(\sum_{k\geq\lceil{(n-4)}/{5}\rceil}a_{1,1}(n,k)t^k+\rho\bigg(\sum_{k\geq\lceil{(n-4)}/{5}\rceil} b_{1,1}(n,k)t^k\bigg)\bigg)\qquad\qquad\textrm{(by (2.2))} \\&=\sum_{n\geq0}\bigg[\sum_{k=1}^1d(1,k)a_{1,1}(k,n)\bigg]t^n+ \rho\bigg\{\sum_{n\geq0}\bigg[\sum_{k=1}^1d(1,k)b_{1,1}(k,n)\bigg]t^n\bigg\} \\&=\sum_{n\geq0}c(2,n)t^n+\rho\bigg(\sum_{n\geq0}d(2,n)t^n\bigg). \end{align*} $$
$$ \begin{align*} L_2&=U^{(1,0)}(L_1)=U_5(M\cdot L_1) \nonumber =\sum_{n=1}^1d(1,n)U_5(M\rho t^n) \nonumber =\sum_{n=1}^1d(1,n)U^{(1,1)}( t^n)\nonumber \\&=\sum_{n=1}^1d(1,n) \bigg(\sum_{k\geq\lceil{(n-4)}/{5}\rceil}a_{1,1}(n,k)t^k+\rho\bigg(\sum_{k\geq\lceil{(n-4)}/{5}\rceil} b_{1,1}(n,k)t^k\bigg)\bigg)\qquad\qquad\textrm{(by (2.2))} \\&=\sum_{n\geq0}\bigg[\sum_{k=1}^1d(1,k)a_{1,1}(k,n)\bigg]t^n+ \rho\bigg\{\sum_{n\geq0}\bigg[\sum_{k=1}^1d(1,k)b_{1,1}(k,n)\bigg]t^n\bigg\} \\&=\sum_{n\geq0}c(2,n)t^n+\rho\bigg(\sum_{n\geq0}d(2,n)t^n\bigg). \end{align*} $$
From Lemma 2.5,
 $$ \begin{align*} \pi(c(2,n))&=\pi(d(1,1))+\pi(a_{1,1}(1,n))\geq1+\bigg\lfloor\frac{5 n+1}{3}\bigg\rfloor , \\ \pi(d(2,n))&=\pi(d(1,1))+\pi(b_{1,1}(1,n))\geq1+\bigg\lfloor\frac{5 n+3}{3}\bigg\rfloor. \end{align*} $$
$$ \begin{align*} \pi(c(2,n))&=\pi(d(1,1))+\pi(a_{1,1}(1,n))\geq1+\bigg\lfloor\frac{5 n+1}{3}\bigg\rfloor , \\ \pi(d(2,n))&=\pi(d(1,1))+\pi(b_{1,1}(1,n))\geq1+\bigg\lfloor\frac{5 n+3}{3}\bigg\rfloor. \end{align*} $$
Thus, the result holds for
![]() $L_{\alpha }$
when
$L_{\alpha }$
when
![]() $\alpha =1, 2$
. We proceed by induction. Suppose that the result holds for
$\alpha =1, 2$
. We proceed by induction. Suppose that the result holds for
![]() $L_{2\alpha }$
. Then, applying (2.2) and (3.5),
$L_{2\alpha }$
. Then, applying (2.2) and (3.5),
 $$ \begin{align*} L_{2\alpha+1}&=U^{(0,0)}(L_{2\alpha})=U_5(K\cdot L_{2\alpha})\\ &=\sum_{n\geq0}c(2\alpha,n) U_5(K t^n)+\sum_{n\geq0}d(2\alpha,n)U_5(K\rho t^n) \\ &=\sum_{n\geq0}c(2\alpha,n)\nonumber \nonumber U^{(0,0)}( t^n)+\sum_{n\geq0}d(2\alpha,n) U^{(0,1)}(t^n)\\ &=\sum_{n\geq0}c(2\alpha,n) \bigg(\sum_{k=\lceil{(n+1)}/{5}\rceil}^{\infty} a_{0,0}(n, k) t^k+\rho\bigg(\sum_{k=\lceil{(n+1)}/{5}\rceil}^{\infty} b_{0,0}(n, k) t^k\bigg)\bigg)\nonumber \\ &\quad+\sum_{n\geq0}d(2\alpha,n) \bigg(\sum_{k=\lceil{(n+1}/{5}\rceil}^{\infty} a_{0,1}(n, k) t^k+\rho\bigg(\sum_{k=\lceil{(n+1)}/{5}\rceil}^{\infty} b_{0,1}(n, k) t^k\bigg)\bigg)\nonumber \\ &=\sum_{n\geq1} \bigg[\sum_{k=0}^{\infty}(c(2\alpha,k) a_{0,0}(k, n) +d(2\alpha,k) a_{0,1}(k, n))\bigg]t^n\nonumber \\&\quad+\rho\bigg\{\sum_{n\geq1}\nonumber \bigg[\sum_{k=0}^{\infty}(c(2\alpha,k) b_{0,0}(k, n) +d(2\alpha,k) b_{0,1}(k, n))\bigg]t^n\bigg\}\\ &=\sum_{n\geq1}c(2\alpha+1,n)t^n+\rho\bigg(\sum_{n\geq1}d(2\alpha+1,n)t^n\bigg). \end{align*} $$
$$ \begin{align*} L_{2\alpha+1}&=U^{(0,0)}(L_{2\alpha})=U_5(K\cdot L_{2\alpha})\\ &=\sum_{n\geq0}c(2\alpha,n) U_5(K t^n)+\sum_{n\geq0}d(2\alpha,n)U_5(K\rho t^n) \\ &=\sum_{n\geq0}c(2\alpha,n)\nonumber \nonumber U^{(0,0)}( t^n)+\sum_{n\geq0}d(2\alpha,n) U^{(0,1)}(t^n)\\ &=\sum_{n\geq0}c(2\alpha,n) \bigg(\sum_{k=\lceil{(n+1)}/{5}\rceil}^{\infty} a_{0,0}(n, k) t^k+\rho\bigg(\sum_{k=\lceil{(n+1)}/{5}\rceil}^{\infty} b_{0,0}(n, k) t^k\bigg)\bigg)\nonumber \\ &\quad+\sum_{n\geq0}d(2\alpha,n) \bigg(\sum_{k=\lceil{(n+1}/{5}\rceil}^{\infty} a_{0,1}(n, k) t^k+\rho\bigg(\sum_{k=\lceil{(n+1)}/{5}\rceil}^{\infty} b_{0,1}(n, k) t^k\bigg)\bigg)\nonumber \\ &=\sum_{n\geq1} \bigg[\sum_{k=0}^{\infty}(c(2\alpha,k) a_{0,0}(k, n) +d(2\alpha,k) a_{0,1}(k, n))\bigg]t^n\nonumber \\&\quad+\rho\bigg\{\sum_{n\geq1}\nonumber \bigg[\sum_{k=0}^{\infty}(c(2\alpha,k) b_{0,0}(k, n) +d(2\alpha,k) b_{0,1}(k, n))\bigg]t^n\bigg\}\\ &=\sum_{n\geq1}c(2\alpha+1,n)t^n+\rho\bigg(\sum_{n\geq1}d(2\alpha+1,n)t^n\bigg). \end{align*} $$
Moreover, using Lemma 2.5, (3.7) and (3.8), we find that
 $$ \begin{align*} \pi(c(2\alpha+1,n))&\geq\min_{k\geq0}\{\pi(c(2\alpha,k))+\pi( a_{0,0}(k, n)), \pi(d(2\alpha,k))+\pi( a_{0,1}(k, n))\}\\ &\geq\alpha+\bigg\lfloor\frac{5 n-2}{3}\bigg\rfloor \end{align*} $$
$$ \begin{align*} \pi(c(2\alpha+1,n))&\geq\min_{k\geq0}\{\pi(c(2\alpha,k))+\pi( a_{0,0}(k, n)), \pi(d(2\alpha,k))+\pi( a_{0,1}(k, n))\}\\ &\geq\alpha+\bigg\lfloor\frac{5 n-2}{3}\bigg\rfloor \end{align*} $$
and
 $$ \begin{align*} \pi(d(2\alpha+1,n))&\geq\min_{k\geq0}\{\pi(c(2\alpha,k))+\pi( b_{0,0}(k, n)), \pi(d(2\alpha,k))+\pi( b_{0,1}(k, n))\} \\ &\geq\alpha+\bigg\lfloor\frac{5 n}{3}\bigg\rfloor. \end{align*} $$
$$ \begin{align*} \pi(d(2\alpha+1,n))&\geq\min_{k\geq0}\{\pi(c(2\alpha,k))+\pi( b_{0,0}(k, n)), \pi(d(2\alpha,k))+\pi( b_{0,1}(k, n))\} \\ &\geq\alpha+\bigg\lfloor\frac{5 n}{3}\bigg\rfloor. \end{align*} $$
Next, we consider
![]() $L_{2\alpha +2}$
. Using (2.2) and (3.6),
$L_{2\alpha +2}$
. Using (2.2) and (3.6),
 $$ \begin{align*} L_{2\alpha+2}&=U^{(1,0)}(L_{2\alpha+1})=U_5(M\cdot L_{2\alpha+1})\nonumber\\ &=\sum_{n\geq1}c(2\alpha+1,n) U_5(M t^n)+\sum_{n\geq1}d(2\alpha+1,n)U_5(M\rho t^n)\nonumber \\ &=\sum_{n\geq1}c(2\alpha+1,n)\nonumber \nonumber U^{(1,0)}( t^n)+\sum_{n\geq1}d(2\alpha+1,n) U^{(1,1)}(t^n)\\ &=\sum_{n\geq1}c(2\alpha+1,n) \bigg(\sum_{k=\lceil{(n-4)}/{5}\rceil}^{\infty} a_{1,0}(n, k) t^k+\rho\bigg(\sum_{k=\lceil{(n-4)}/{5}\rceil}^{\infty} b_{1,0}(n, k) t^k\bigg)\bigg)\nonumber \\ &\quad+\sum_{n\geq1}d(2\alpha+1,n) \bigg(\sum_{k=\lceil{(n-4)}/{5}\rceil}^{\infty} a_{1,1}(n, k) t^k+\rho\bigg(\sum_{k=\lceil{(n-4)}/{5}\rceil}^{\infty} b_{1,1}(n, k) t^k\bigg)\bigg)\nonumber \\ &=\sum_{n\geq0} \bigg[\sum_{k=1}^{\infty}(c(2\alpha+1,k) a_{1,0}(k, n) +d(2\alpha+1,k) a_{1,1}(k, n))\bigg]t^n\nonumber \\&\quad+\rho\bigg\{\sum_{n\geq0}\nonumber \bigg[\sum_{k=1}^{\infty}(c(2\alpha+1,k) b_{1,0}(k, n) +d(2\alpha+1,k) b_{1,1}(k, n))\bigg]t^n\bigg\}\\ &=\sum_{n\geq0}c(2\alpha+2,n)t^n+\rho\bigg(\sum_{n\geq0}d(2\alpha+2,n)t^n\bigg). \end{align*} $$
$$ \begin{align*} L_{2\alpha+2}&=U^{(1,0)}(L_{2\alpha+1})=U_5(M\cdot L_{2\alpha+1})\nonumber\\ &=\sum_{n\geq1}c(2\alpha+1,n) U_5(M t^n)+\sum_{n\geq1}d(2\alpha+1,n)U_5(M\rho t^n)\nonumber \\ &=\sum_{n\geq1}c(2\alpha+1,n)\nonumber \nonumber U^{(1,0)}( t^n)+\sum_{n\geq1}d(2\alpha+1,n) U^{(1,1)}(t^n)\\ &=\sum_{n\geq1}c(2\alpha+1,n) \bigg(\sum_{k=\lceil{(n-4)}/{5}\rceil}^{\infty} a_{1,0}(n, k) t^k+\rho\bigg(\sum_{k=\lceil{(n-4)}/{5}\rceil}^{\infty} b_{1,0}(n, k) t^k\bigg)\bigg)\nonumber \\ &\quad+\sum_{n\geq1}d(2\alpha+1,n) \bigg(\sum_{k=\lceil{(n-4)}/{5}\rceil}^{\infty} a_{1,1}(n, k) t^k+\rho\bigg(\sum_{k=\lceil{(n-4)}/{5}\rceil}^{\infty} b_{1,1}(n, k) t^k\bigg)\bigg)\nonumber \\ &=\sum_{n\geq0} \bigg[\sum_{k=1}^{\infty}(c(2\alpha+1,k) a_{1,0}(k, n) +d(2\alpha+1,k) a_{1,1}(k, n))\bigg]t^n\nonumber \\&\quad+\rho\bigg\{\sum_{n\geq0}\nonumber \bigg[\sum_{k=1}^{\infty}(c(2\alpha+1,k) b_{1,0}(k, n) +d(2\alpha+1,k) b_{1,1}(k, n))\bigg]t^n\bigg\}\\ &=\sum_{n\geq0}c(2\alpha+2,n)t^n+\rho\bigg(\sum_{n\geq0}d(2\alpha+2,n)t^n\bigg). \end{align*} $$
Then again by Lemma 2.5, (3.7) and (3.8),
 $$ \begin{align*} \pi(c(2\alpha+2,n))&\geq\min_{k\geq1}\{\pi(c(2\alpha+1,k))+\pi( a_{1,0}(k, n)), \pi(d(2\alpha+1,k))+\pi( a_{1,1}(k, n))\}\nonumber\\ &\geq\alpha+1+\bigg\lfloor\frac{5 n+1}{3}\bigg\rfloor \nonumber \end{align*} $$
$$ \begin{align*} \pi(c(2\alpha+2,n))&\geq\min_{k\geq1}\{\pi(c(2\alpha+1,k))+\pi( a_{1,0}(k, n)), \pi(d(2\alpha+1,k))+\pi( a_{1,1}(k, n))\}\nonumber\\ &\geq\alpha+1+\bigg\lfloor\frac{5 n+1}{3}\bigg\rfloor \nonumber \end{align*} $$
and
 $$ \begin{align*} \pi(d(2\alpha+2,n))&\geq\min_{k\geq1}\{\pi(c(2\alpha+1,k))+\pi( b_{1,0}(k, n)), \pi(d(2\alpha+1,k))+\pi( b_{1,1}(k, n))\}\nonumber\\ &\geq\alpha+1+\bigg\lfloor\frac{5 n+3}{3}\bigg\rfloor \nonumber. \end{align*} $$
$$ \begin{align*} \pi(d(2\alpha+2,n))&\geq\min_{k\geq1}\{\pi(c(2\alpha+1,k))+\pi( b_{1,0}(k, n)), \pi(d(2\alpha+1,k))+\pi( b_{1,1}(k, n))\}\nonumber\\ &\geq\alpha+1+\bigg\lfloor\frac{5 n+3}{3}\bigg\rfloor \nonumber. \end{align*} $$
Thus, the result holds for
![]() $L_{2\alpha +2}$
. This proves Theorem 3.3 by induction.
$L_{2\alpha +2}$
. This proves Theorem 3.3 by induction.
Corollary 3.4. For
![]() $\alpha \geq 1$
,
$\alpha \geq 1$
,
Note that (3.4) together with Corollary 3.4 implies (1.5). Thus, the proof of Theorem 1.1 is complete.