A CONJECTURE OF MERCA ON CONGRUENCES MODULO POWERS OF 2 FOR PARTITIONS INTO DISTINCT PARTS

Abstract

Let 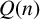$Q(n)$ denote the number of partitions of n into distinct parts. Merca [‘Ramanujan-type congruences modulo 4 for partitions into distinct parts’, An. Şt. Univ. Ovidius Constanţa 30(3) (2022), 185–199] derived some congruences modulo 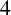$4$ and 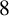$8$ for 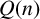$Q(n)$ and posed a conjecture on congruences modulo powers of 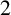$2$ enjoyed by 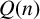$Q(n)$. We present an approach which can be used to prove a family of internal congruence relations modulo powers of 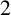$2$ concerning 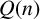$Q(n)$. As an immediate consequence, we not only prove Merca’s conjecture, but also derive many internal congruences modulo powers of 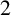$2$ satisfied by 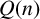$Q(n)$. Moreover, we establish an infinite family of congruence relations modulo 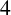$4$ for 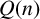$Q(n)$.

1 Introduction

A partition $\pi $ of a positive integer n is a finite weakly decreasing sequence of positive integers $\pi _1\geq \pi _2\geq \cdots \geq \pi _r$ such that $\sum _{i=1}^r\pi _i=n$ . The $\pi _i$ are called the parts of the partition $\pi $ . Let $p(n)$ denote the number of partitions of n with the convention that $p(0)=1$ . The generating function of $p(n)$ , derived by Euler, is given by

$$ \begin{align*} \sum_{n=0}^{\infty} p(n)q^n=\dfrac{1}{(q;q)_{\infty}}, \end{align*} $$

where, here and throughout this paper, we always assume that q is a complex number such that $|q|<1$ and adopt the customary notation:

$$ \begin{align*} (a;q)_{\infty}=\prod_{j=0}^{\infty}(1-aq^j). \end{align*} $$

In 1919, Ramanujan discovered three celebrated congruences for the partition function $p(n)$ (see [4]), which were later confirmed by Atkin [2] and Watson [15]: for any $n\geq 0$ and $\alpha \geq 1$ ,

(1.1) $$ \begin{align} \kern3pt p(5^{\alpha} n+\delta_{5,\alpha}) &\equiv0\pmod{5^{\alpha}}, \end{align} $$

(1.2) $$ \begin{align} \kern24pt p(7^{\alpha} n+\delta_{7,\alpha}) &\equiv0\pmod{7^{\lfloor\alpha/2\rfloor+1}}, \end{align} $$

(1.3) $$ \begin{align} p(11^{\alpha} n+\delta_{11,\alpha}) &\equiv0\pmod{11^{\alpha}}, \end{align} $$

where $\delta _{p,\alpha }$ is the least positive integer satisfying $24\delta _{p,\alpha }\equiv 1\pmod {p^{\alpha }}$ with ${p\in \{5,7,11\}}$ . Since then, congruence properties for various partition functions have been a hot topic in the theory of partitions and have motivated a large amount of research.

Another ingredient of the theory of partitions is the study of partition identities. In 1748, Euler [7] proved the most well-known partition theorem which states that there are as many partitions of n into distinct parts as into odd parts. In terms of the generating function,

(1.4) $$ \begin{align} \sum_{n=0}^{\infty} Q(n)q^n=(-q;q)_{\infty}=\dfrac{1}{(q;q^2)_{\infty}}=\dfrac{(q^2;q^2)_{\infty}}{(q;q)_{\infty}}, \end{align} $$

where $Q(n)$ denotes the number of partitions of n into distinct parts. According to Euler’s pentagonal number theorem [1, page 17, (1.4.11)],

$$ \begin{align*} (q;q)_{\infty}=\sum_{n=-\infty}^{\infty}(-1)^nq^{n(3n-1)/2}, \end{align*} $$

we find that almost all values of $Q(n)$ are even, that is,

(1.5) $$ \begin{align} \lim_{X\rightarrow\infty}\dfrac{\#\{0\leq n\leq X\colon Q(n)\equiv0\pmod{2}\}}{X}=1. \end{align} $$

Indeed, $Q(n)$ is odd if and only if n is a generalised pentagonal number. Motivated by (1.1)–(1.5), many scholars subsequently investigated congruence properties and arithmetic density properties of $Q(n)$ . For instance, in 1997, Gordon and Ono [8] proved the striking result that for any positive integer m, $Q(n)$ is divisible by $2^m$ for almost all nonnegative integers n, that is,

(1.6) $$ \begin{align} \lim_{X\rightarrow\infty}\dfrac{\#\{0\leq n\leq X\colon Q(n)\equiv0\pmod{2^m}\}}{X}=1. \end{align} $$

The identity (1.6) is a powerful result on the arithmetic properties of $Q(n)$ . However, it is not a constructive result and the theory of modular forms used in the proof of (1.6) cannot be applied to derive the explicit congruences enjoyed by $Q(n)$ . Therefore, it is still of interest to find explicit congruences for $Q(n)$ .

In a recent paper, Merca [9] derived some congruences modulo $4$ and $8$ for $Q(n)$ by using Smoot’s Mathematica implementation [13] of Radu’s algorithm [12] on Ramanujan–Kolberg identities for partition functions. At the end of his paper, Merca posed the following conjecture on congruences modulo powers of 2 for $Q(n)$ .

Conjecture 1.1 (Merca [9], Conjecture).

Let $(p,k)\in S$ . For any $n\not \equiv 0\pmod {p}$ ,

$$ \begin{align*} Q{\bigg(pn+\dfrac{p^2-1}{24}\bigg)}\equiv0\pmod{2^k}, \end{align*} $$

where

(1.7) $$ \begin{align} S\in\{ &(11,5),(13,6),(17,8),(19,9),(23,11),(31,3),(37,6),\nonumber\\ &(41,8),(43,9),(47,11),(59,6),(61,6),(67,10),(71,13),\nonumber\\ &(79,3),(83,5),(89,9),(103,3),(107,6),(109,6),(113,9)\}. \end{align} $$

In this paper, we prove the following result.

Theorem 1.2. Let S be defined as in (1.7). Then for any $(p,k)\in S$ ,

(1.8) $$ \begin{align} \sum_{n=0}^{\infty} Q{\bigg(pn+\dfrac{p^2-1}{24}\bigg)}q^n\equiv c_p\sum_{n=0}^{\infty} Q(n)q^{pn}\pmod{2^k}, \end{align} $$

where $c_p$ is given in Table 1.

Table 1 A table of values of $c_p$ .

As an immediate consequence of (1.8), we obtain the following congruences and internal congruences enjoyed by $Q(n)$ , which confirms Conjecture 1.1.

Corollary 1.3. Let S be defined as in (1.7). Then for any $(p,k)\in S$ and $1\leq i\leq p-1$ ,

$$ \begin{align*} Q\kern1pt{\bigg(p^2n+\dfrac{(24i+p)p-1}{24}\bigg)}\equiv0\pmod{2^k}. \end{align*} $$

Moreover, for any $n\geq 0$ ,

$$ \begin{align*} Q{\bigg(p^2n+\dfrac{p^2-1}{24}\bigg)}\equiv c_pQ(n)\pmod{2^k}, \end{align*} $$

where $c_p$ is given in Table 1.

The following theorem shows that there are an infinite family of congruence relations of the form (1.8) satisfied by $Q(n)$ .

Theorem 1.4. Let $p\geq 5$ be a prime number. If $\big(\frac{-24}{p}\big)=-1$ , then

(1.9) $$ \begin{align} \sum_{n=0}^{\infty} Q{\bigg(pn+\dfrac{p^2-1}{24}\bigg)}q^n\equiv(-1)^{(\pm p-1)/6}\sum_{n=0}^{\infty} Q(n)q^{pn}\pmod{4}, \end{align} $$

where $\big (\frac {\cdot }{p}\big )$ is the Legendre symbol and

(1.10) $$ \begin{align} (\pm p-1)/6= \begin{cases} (p-1)/6 &\textrm{if } p\equiv1\pmod{6},\\ (-p-1)/6 &\textrm{if } p\equiv5\pmod{6}. \end{cases} \end{align} $$

The rest of this paper is organised as follows. In Section 2, we collect some notation and terminology on modular forms. The proof of Theorem 1.2 is presented in Section 3 and that of Theorem 1.4 in Section 4. Finally, we pose a conjecture on congruence relations for $Q(n)$ modulo $4$ which strengthens both (1.9) and a result of Merca.

2 Preliminaries

We first recall some terminology from the theory of modular forms. The full modular group is given by

$$ \begin{align*} \Gamma=\bigg\{\begin{pmatrix}a &b\\ c &d\end{pmatrix}\colon a, b, c, d\in\mathbb{Z}, \text{ and } ad-bc=1\bigg\}, \end{align*} $$

and for a positive integer N, the congruence subgroup $\Gamma _0(N)$ is defined by

$$ \begin{align*} \Gamma_0(N)=\bigg\{\begin{pmatrix}a &b\\ c &d\end{pmatrix}\in\Gamma \colon c\equiv 0\pmod{N}\bigg\}. \end{align*} $$

Let $\gamma $ be the matrix $(\begin {smallmatrix}a &b\\ c &d\end {smallmatrix})$ from now on. Then $\gamma $ acts on $\tau \in \mathbb {C}$ by the linear fractional transformation

$$ \begin{align*} \gamma\tau = \frac{a\tau+b}{c\tau+d} \quad \text{and} \quad \gamma\infty =\lim_{\tau\rightarrow \infty} \gamma\tau. \end{align*} $$

Let N, k be positive integers and $\mathbb {H}=\{\tau \in \mathbb {C}\colon \mathrm {Im}(\tau )>0\}$ . A holomorphic function $f\colon \mathbb {H}\rightarrow \mathbb {C}$ is called a modular function of weight k for $\Gamma _0(N)$ if it satisfies the following two conditions:

1. (1) for all $\gamma \in \Gamma _0(N)$ , $f(\gamma \tau )=(c\tau +d)^kf(\tau )$ ;

2. (2) for any $\gamma \in \Gamma $ , $(c\tau +d)^{-k}f(\gamma \tau )$ has a Fourier expansion of the form

   $$ \begin{align*} (c\tau+d)^{-k}f(\gamma\tau)=\sum_{n=n_{\gamma}}^{\infty} a(n)q_{w_{\gamma}}^n, \end{align*} $$

   where $a(n_{\gamma })\neq 0$ , $q_{w_{\gamma }}=e^{2\pi i\tau /w_{\gamma }}$ and $w_{\gamma }={N}/{\gcd (c^2, N)}$ .

In particular, if $n_{\gamma } \geq 0$ for all $\gamma \in \Gamma $ , then we call f a modular form of weight k for $\Gamma _0(N)$ . A modular function with weight 0 for $\Gamma _0(N)$ is referred to as a modular function for $\Gamma _0(N)$ . For a modular function $f(\tau )$ of weight k with respect to $\Gamma _0(N)$ , the order of $f(\tau )$ at the cusp $a/c\in \mathbb {Q}\cup \{\infty \}$ is defined by

$$ \begin{align*} \mathrm{ord}_{a/c}(f)=n_{\gamma} \end{align*} $$

for some $\gamma \in \Gamma $ such that $\gamma \infty =a/c$ ; $\mathrm {ord}_{a/c}(f)$ is well defined (see [6, page 72]).

Radu [12] developed the Ramanujan–Kolberg algorithm to derive the Ramanujan– Kolberg identities on a class of partition functions defined in terms of eta-quotients using modular functions for $\Gamma _0(N)$ (see [11]). Smoot [13] developed a Mathematica package $\mathtt {RaduRK}$ to implement Radu’s algorithm.

Let the partition function $a(n)$ be defined by

(2.1) $$ \begin{align} \sum_{n=0}^{\infty} a(n)q^n=\prod_{\delta|M} (q^{\delta}, q^{\delta})_{\infty}^{r_{\delta}}, \end{align} $$

where M, $\delta $ are positive integers and $r_{\delta }$ are integers. For any $m\geq 1$ and $0\leq t\leq m-1$ , Radu [12] defined

$$ \begin{align*} g_{m,t}(\tau) = q^{{(t+\ell)}/{m}}\sum\limits_{n=0}^{\infty} a(mn+t)q^n, \end{align*} $$

where

$$ \begin{align*} \ell=\frac{1}{24}\sum\limits_{\delta|M}\delta r_{\delta}, \end{align*} $$

and gave a criterion for a function involving $g_{m,t}(\tau )$ to be a modular function with respect to $\Gamma _0(N)$ , where N satisfies the following conditions, with $\kappa =\gcd (1-m^2, 24)$ :

1. (1) for every prime p, $p \mid m$ implies $p \mid N$ ;

2. (2) for every $\delta $ dividing M with $r_{\delta }\neq 0$ , $\delta \mid M$ implies $\delta \mid mN$ ;

3. (3) $\kappa mN^2\sum _{\delta |M}{r_{\delta }}/{\delta }\equiv 0\pmod {24}$ ;

4. (4) $\kappa N \sum _{\delta |M} r_{\delta } \equiv 0\pmod {8}$ ;

5. (5) ${24 m}/{\gcd (\kappa (-24 t-\sum _{\delta |M}\delta r_{\delta }), 24 m)} \mid N ;$

6. (6) if $2 \mid m$ , then $\kappa N\equiv 0\pmod {4}$ and $8 \mid Ns$ , or $2 \mid s$ and $8 \mid N(1-j)$ , where $\prod _{\delta |M} \delta ^{|r_{\delta }|}=2^sj$ and $j, s\in \mathbb {Z}$ with j odd.

Given a positive integer n and an integer x, we denote by $[x]_n$ the residue class of x modulo n. Let

$$ \begin{align*} \mathbb{Z}_n^*=\{[x]_n\in\mathbb{Z}_n : \gcd(x,n)=1\} \quad \text{and} \quad \mathbb{S}_n=\{y^2: y\in\mathbb{Z}_n^*\}. \end{align*} $$

Define the set

$$ \begin{align*} P_m(t)=\bigg\{\bigg[ts+\frac{s-1}{24}\sum_{\delta|M}\delta r_{\delta}\bigg]_m : s\in\mathbb{S}_{24m}\bigg\}. \end{align*} $$

Recall that the Dedekind eta-function $\eta (\tau )$ is defined by

$$ \begin{align*} \eta(\tau)=q^{{1}/{24}}\prod_{n=1}^{\infty}(1-q^n), \end{align*} $$

where $q=e^{2\pi i \tau }$ and $\tau \in \mathbb {H}$ .

Theorem 2.1 [12, Theorem 45].

For a partition function $a(n)$ defined as in (2.1), and integers $m\geq 1, 0\leq t\leq m-1$ , suppose that N is a positive integer satisfying the conditions (1)–(6). Let

$$ \begin{align*} F(\tau)=\prod_{\delta|N} \eta^{s_{\delta}}(\delta\tau)\prod_{t'\in P_{m}(t)}g_{m,t'}(\tau), \end{align*} $$

where $s_{\delta }$ are integers. Then $F(\tau )$ is a modular function for $\Gamma _0(N)$ if and only if the $s_{\delta }$ satisfy the following conditions:

1. (1) $|P_m(t)| \sum _{\delta |M}r_{\delta }+\sum _{\delta |N} s_{\delta } =0;$

2. (2) $\sum _{t'\in P_m(t)}{(1-m^2)(24t'+\sum _{\delta |M}\delta r_{\delta })}/{m} +|P_m(t)|m\sum _{\delta |M}\delta r_{\delta }+\sum _{\delta |N}\delta s_{\delta }\equiv 0\pmod {24};$

3. (3) $|P_m(t)|mN\sum _{\delta |M}{r_{\delta }}/{\delta }+\sum _{\delta |N} ({N}/{\delta })s_{\delta } \equiv 0\pmod {24};$

4. (4) ${(\prod _{\delta |M}(m\delta )^{|r_{\delta }|})}^{|P_{m}(t)|}\prod _{\delta |N}\delta ^{|s_{\delta }|}$ is a square.

Radu [12, Theorem 47] also gave lower bounds for the orders of $F(\tau )$ at cusps of $\Gamma _0(N)$ .

Theorem 2.2. For a partition function $a(n)$ defined as in (2.1) and integers $m\geq 1$ , $0\leq t\leq m-1$ , let

$$ \begin{align*} F(\tau)=\prod_{\delta|N} \eta^{s_{\delta}}(\delta\tau)\prod_{t'\in P_{m}(t)}g_{m,t'}(\tau) \end{align*} $$

be a modular function for $\Gamma _0(N)$ , where $s_{\delta }$ are integers and N satisfies the conditions (1)–(6). Let $\{s_1, s_2,\ldots ,s_{\epsilon }\}$ be a complete set of inequivalent cusps of $\Gamma _0(N)$ and, for $1\leq i \leq \epsilon $ , let $\gamma _i\in \Gamma $ be such that $\gamma _i\infty = s_i$ . Then

$$ \begin{align*} \mathrm{ord}_{s_i}(F(\tau)) \geq \frac{N}{\gcd(c^2, N)}(|P_m(t)|p(\gamma_i)+p^*(\gamma_i)), \end{align*} $$

where

$$ \begin{align*} p(\gamma_i)=\min_{\lambda\in\{0, 1, \ldots, m-1\}}\frac{1}{24}\sum_{\delta|M} r_{\delta}\frac{\gcd^2(\delta(a+\kappa\lambda c), mc)}{\delta m} \end{align*} $$

and

$$ \begin{align*} p^*(\gamma_i)=\frac{1}{24}\sum_{\delta|N}s_{\delta}\frac{\gcd^2(\delta, c)}{\delta}. \end{align*} $$

The following theorem of Sturm [14, Theorem 1] plays an important role in proving congruences using the theory of modular forms.

Theorem 2.3. Let k be an integer and $g(\tau )=\sum _{n=0}^{\infty } c(n)q^n$ a modular form of weight k for $\Gamma _0(N)$ . For any given positive integer u, if $c(n)\equiv 0\pmod {u}$ holds for all $n\leq ({kN}/{12})\prod _{p|N, \, p\mathrm {~prime}}{(1+{1}/{p})}$ , then $c(n)\equiv 0\pmod {u}$ holds for any $n\geq 0$ .

3 Proof of Theorem 1.2

This section is devoted to the proof of Theorem 1.2. The following lemma plays a vital role in the proof of Theorem 1.2.

Lemma 3.1. Let $p$ be a prime with $p\ge5$ and define $k_1 = \lceil(p^2-1)/48p\rceil$ and ${k_2 = \lceil(p^2-1)/48p^2\rceil}$ . Then for any constant c,

$$ \begin{align*} \frac{\eta^{24k_1}(\tau)\eta^{16k_2}(2p\tau)}{\eta^{8k_2}(p\tau)} {\bigg(q^{{p}/{24}}\dfrac{\eta(p\tau)}{\eta(2p\tau)}\sum_{n=0}^{\infty} Q{\bigg(pn+\frac{p^2-1}{24}\bigg)}q^n-c\bigg)} \end{align*} $$

is a modular form of weight $12k_1+4k_2$ for $\Gamma _0(2p)$ .

Proof. Recall that the generating function of $Q(n)$ is

$$ \begin{align*} \sum_{n=0}^{\infty} Q(n)q^n=\frac{(q^2; q^2)_{\infty}}{(q; q)_{\infty}}. \end{align*} $$

Taking $M=2$ , $(r_1, r_2)=(-1,1)$ , $m=p$ , $t=(p^2-1)/24$ in Theorem 2.1, one can find that $N=2p$ satisfies the conditions (1)–(6), and for $(s_1, s_2, s_p, s_{2p})=(0,0,1, -1)$ ,

$$ \begin{align*} F(\tau)=q^{{p}/{24}}\frac{\eta(p\tau)}{\eta(2p\tau)} \sum_{n=0}^{\infty} Q{\bigg(pn+\frac{p^2-1}{24}\bigg)}q^n \end{align*} $$

is a modular function for $\Gamma _0(2p)$ .

By Theorem 2.2, we derive lower bounds for the orders of $F(\tau )$ at the cusps of $\Gamma _0(2p)$ :

$$ \begin{align*} \mathrm{ord}_0(F(\tau)) \geq-\frac{p^2-1}{24}, &\quad \mathrm{ord}_{1/2}(F(\tau))\geq -\frac{1}{24p},\\ \mathrm{ord}_{1/p}(F(\tau)) \geq \frac{2p^2-1}{24p}, &\quad \mathrm{ord}_{\infty}(F(\tau))\geq -\frac{p^2-1}{24p}, \end{align*} $$

which implies that

$$ \begin{align*} \mathrm{ord}_0(F(\tau)-c) \geq -\frac{p^2-1}{24}, &\quad \mathrm{ord}_{1/2}(F(\tau)-c) \geq 0,\\ \mathrm{ord}_{1/p}(F(\tau)-c) \geq 0, &\quad \mathrm{ord}_{\infty}(F(\tau)-c) \geq -\frac{p^2-1}{24p}. \end{align*} $$

By [10, Theorems 1.64 and 1.65], one easily shows

$$ \begin{align*} F_1(\tau)=\eta^{24}(\tau) \quad \text{and} \quad F_2(\tau)=\frac{\eta^{16}(2p\tau)}{\eta^8(p\tau)} \end{align*} $$

are modular forms with weight 12 and 4 for $\Gamma _0(2p)$ , respectively, and the orders at the cusps of $\Gamma _0(2p)$ are

$$ \begin{align*} \mathrm{ord}_0(F_1(\tau)) =2p, \quad \mathrm{ord}_{1/2}(F_1(\tau)) =p, &\quad \mathrm{ord}_{1/p}(F_1(\tau)) =2, \quad \mathrm{ord}_{\infty}(F_1(\tau)) =1,\\ \mathrm{ord}_0(F_2(\tau)) =0, \quad \mathrm{ord}_{1/2}(F_2(\tau)) =1, &\quad \mathrm{ord}_{1/p}(F_2(\tau)) =0, \quad \mathrm{ord}_{\infty}(F_2(\tau)) =p. \end{align*} $$

Therefore, the orders of $F^{k_1}_1(\tau )F^{k_2}_2(\tau )F(\tau )$ at all cusps of $\Gamma _0(2p)$ are nonnegative, and so $F^{k_1}_1(\tau )F^{k_2}_2(\tau )F(\tau )$ is a modular form with weight $12k_2+4k_2$ for $\Gamma _0(2p)$ . This completes the proof.

Proof of Theorem 1.2.

Fix $k\ge 1$ . By Lemma 3.1 and Sturm’s theorem, to prove

$$ \begin{align*} \dfrac{(q^p;q^p)_{\infty}}{(q^{2p};q^{2p})_{\infty}} \sum_{n=0}^{\infty} Q{\bigg(pn+\frac{p^2-1}{24}\bigg)}q^n-c_p\equiv 0\pmod{2^k}, \end{align*} $$

we only need to check that the coefficients of the first $l_p=(p+1)(3k_1+k_2)$ terms of the expansion of

$$ \begin{align*} \frac{\eta^{24k_1}(\tau)\eta^{16k_2}(2p\tau)}{\eta^{8k_2}(p\tau)} {\bigg(q^{{p}/{24}}\dfrac{\eta(p\tau)}{\eta(2p\tau)} \sum_{n=0}^{\infty} Q{\bigg(pn+\frac{p^2-1}{24}\bigg)}q^n-c_p\bigg)} \end{align*} $$

are congruent to 0 modulo $2^k$ . Here, $k_1$ and $k_2$ are defined in Lemma 3.1 and the corresponding $l_p$ are displayed in Table 2. This information allows us to do the computations to complete the proof of Theorem 1.2.

Table 2 A table of values of $l_p$ .

4 Proof of Theorem 1.4

In this section, we give a proof of Theorem 1.4. Before starting the proof, we need to introduce Ramanujan’s theta function, given by

(4.1) $$ \begin{align} f(a,b)=\sum_{n=0}^{\infty} a^{n(n+1)/2}b^{n(n-1)/2}=(-a,-b,ab;ab)_{\infty},\quad|ab|<1, \end{align} $$

where the last identity in (4.1) is the celebrated Jacobi triple product [1, page 17, (1.4.8)]. Two important cases of $f(a,b)$ are

(4.2) $$ \begin{align} \varphi(q) &:=f(q,q)=\sum_{n=0}^{\infty} q^{n^2}=\dfrac{(q^2;q^2)_{\infty}^5}{(q;q)_{\infty}^2(q^4;q^4)_{\infty}^2},\\ f(-q) &:=f(-q,-q^2)=\sum_{n=-\infty}^{\infty} q^{n(3n+1)/2}=(q;q)_{\infty}.\nonumber \end{align} $$

Replacing q by $-q$ in (4.2) yields

$$ \begin{align*} \varphi(-q)=\dfrac{(q;q)_{\infty}^2}{(q^2;q^2)_{\infty}}. \end{align*} $$

The following p-dissections for $\varphi (-q)$ and $f(-q)$ play an important role in the proof of Theorem 1.4.

Lemma 4.1. Let $p\geq 5$ be a prime number. Then

(4.3) $$ \begin{align} \varphi(-q) &=\varphi({-}q^{p^2})+2\sum_{j=1}^{(p-1)/2}q^{{\kern1.2pt}j^2} f({-}q^{p^2+2pj},-q^{p^2-2pj}), \end{align} $$

(4.4) $$ \begin{align} f(-q) &=\sum_{\substack{k=-(p-1)/2\\ k\neq(\pm p-1)/6}}^{(p-1)/2}(-1)^kq^{k(3k+1)/2} f({-}q^{(3p^2+(6k+1)p)/2},-q^{(3p^2-(6k+1)p)/2})\nonumber\\ &\quad+(-1)^{(\pm p-1)/6}q^{(p^2-1)/24}f({-}q^{p^2}), \end{align} $$

where $(\pm p-1)/6$ is defined as in (1.10). Further, for $-(p-1)/2\leq k\leq (p-1)/2$ and $k\neq (\pm p-1)/6$ ,

$$ \begin{align*} \dfrac{3k^2+k}{2}\not\equiv\dfrac{p^2-1}{24}\pmod{p}. \end{align*} $$

Proof. The identity (4.3) follows immediately from [3, page 49]. The identity (4.4) appears in [5, Theorem 2.2].

Proof of Theorem 1.4.

From (1.4), we find that

(4.5) $$ \begin{align} \sum_{n=0}^{\infty} Q(n)q^n=\dfrac{(q^2;q^2)_{\infty}}{(q;q)_{\infty}}=\dfrac{(q^2;q^2)_{\infty}^2}{(q;q)_{\infty}^4}\cdot \dfrac{(q;q)_{\infty}^3}{(q^2;q^2)_{\infty}}\equiv\varphi(-q)\cdot f(-q)\pmod{4}. \end{align} $$

For a prime $p\geq 5$ , $0\leq j\leq (p-1)/2$ , $-(p-1)/2\leq k\leq (p-1)/2$ , assume that

$$ \begin{align*} j^2+\dfrac{3k^2+k}{2}\equiv\dfrac{p^2-1}{24}\pmod{p}, \end{align*} $$

which implies that

$$ \begin{align*} 24j^2+(6k+1)^2\equiv0\pmod{p}. \end{align*} $$

Since $\big(\frac{-24}{p}\big)=-1$ , we get $j=0$ and $k=(\pm p-1)/6$ . Substituting (4.3) and (4.4) into (4.5), we find that

$$ \begin{align*} \sum_{n=0}^{\infty} Q{\bigg(pn+\dfrac{p^2-1}{24}\bigg)}q^n &\equiv(-1)^{(\pm p-1)/6}\varphi({-}q^p)f({-}q^p)\nonumber\\ &\equiv(-1)^{(\pm p-1)/6}\sum_{n=0}^{\infty} Q(n)q^{pn}\pmod{4}, \end{align*} $$

where we have used (4.5) in the last congruence. The congruence (1.9) follows. This completes the proof of Theorem 1.4.

5 Concluding remarks

One can use Lemma 3.1 to establish congruence relations satisfied by $Q(n)$ similar to (1.8) for other primes p. For example,

$$ \begin{align*} \sum_{n=0}^{\infty} Q(127n+672)q^n &\equiv\sum_{n=0}^{\infty} Q(n)q^{127n}\pmod{2^3},\\ \sum_{n=0}^{\infty} Q(131n+715)q^n &\equiv43\sum_{n=0}^{\infty} Q(n)q^{131n}\pmod{2^7},\\ \sum_{n=0}^{\infty} Q(137n+782)q^n &\equiv71\sum_{n=0}^{\infty} Q(n)q^{137n}\pmod{2^8},\\ \sum_{n=0}^{\infty} Q(139n+805)q^n &\equiv803\sum_{n=0}^{\infty} Q(n)q^{139n}\pmod{2^{10}}. \end{align*} $$

However, the corresponding bound $l_p$ will become much larger as p increases.

Merca [9] proved the following infinite family of congruences modulo $4$ for $Q(n)$ .

Theorem 5.1. Let $p\geq 5$ be a prime number such that $p\not \equiv 1\pmod {24}$ . Then for any $n\not \equiv 0\pmod {p}$ ,

(5.1) $$ \begin{align} Q{\bigg(pn+\dfrac{p^2-1}{24}\bigg)}\equiv0\pmod{4}. \end{align} $$

The congruence (1.8) together with numerical evidence suggests the following conjecture, which contains (1.9) and (5.1) as special cases.

Conjecture 5.2. Let $p\geq 5$ be a prime number such that $p\not \equiv 1\pmod {24}$ . Then

$$ \begin{align*} \sum_{n=0}^{\infty} Q{\bigg(pn+\dfrac{p^2-1}{24}\bigg)}q^n\equiv c_p\sum_{n=0}^{\infty} Q(n)q^{pn}\pmod{4}, \end{align*} $$

where $c_p=-1$ or $1$ .