Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T00:25:07.805Z Has data issue: false hasContentIssue false
  • English
  • Français

THE CONNECTION BETWEEN PSEUDO ALMOST PERIODIC FUNCTIONS DEFINED ON TIME SCALES AND ON THE REAL LINE

Part of: Harmonic analysis in one variable Real functions: Miscellaneous topics

Published online by Cambridge University Press:  22 February 2017

CHAO-HONG TANG  and
HONG-XU LI
CHAO-HONG TANG
Affiliation:
Department of Mathematics, Sichuan University, Chengdu, Sichuan 610064, PR China email 836188248@qq.com
HONG-XU LI*
Affiliation:
Department of Mathematics, Sichuan University, Chengdu, Sichuan 610064, PR China email hoxuli@scu.edu.cn
*
✉hoxuli@scu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A necessary and sufficient condition for a continuous function 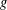$g$ to be almost periodic on time scales is the existence of an almost periodic function 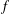$f$ on 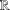$\mathbb{R}$ such that 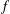$f$ is an extension of 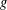$g$. Our aim is to study this question for pseudo almost periodic functions. We prove the necessity of the condition for pseudo almost periodic functions. An example is given to show that the sufficiency of the condition does not hold for pseudo almost periodic functions. Nevertheless, the sufficiency is valid for uniformly continuous pseudo almost periodic functions. As applications, we give some results on the connection between the pseudo almost periodic (or almost periodic) solutions of dynamic equations on time scales and of the corresponding differential equations.

Keywords

almost periodicpseudo almost periodictime scales

MSC classification

Primary: 42A75: Classical almost periodic functions, mean periodic functions
Secondary: 26E70: Real analysis on time scales or measure chains
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 95 , Issue 3 , June 2017 , pp. 482 - 494
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

This work is supported by National Natural Science Foundation (NNSF) of China (Grant Nos. 11471227, 11561077).

References

Cabada, A. and Vivero, D. R., ‘Expression of the Lebesgue 𝛥-integral on time scales as a usual Lebesgue integral. Application to the calculus of 𝛥-antiderivatives’, J. Math. Anal. Appl. 43 (2006), 194–207.Google Scholar
Hilger, S., Ein Maßkettenkalkül mit Anwendung auf Zentrumsmanningfaltigkeiten, PhD Thesis, Universität Würzburg, 1988.Google Scholar
Li, H. X., ‘Pseudo almost periodic sequences and some nonlinear differential equations with piecewise constant argument’, Nonlinear Funct. Anal. Appl. 10 (2005), 479–493.Google Scholar
Li, Y. K. and Wang, C., ‘Almost periodic functions on time scales and applications’, Discrete Dyn. Nat. Soc. 2011 (2011), 727068.Google Scholar
Li, Y. K. and Wang, C., ‘Uniformly almost periodic functions and almost periodic solutions to dynamic equations on time scales’, Abstr. Appl. Anal. 2011 (2011), 341520.Google Scholar
Li, Y. K. and Wang, C., ‘Pseudo almost periodic functions and pseudo almost periodic solutions to dynamic equations on time scales’, Adv. Difference Equ. 2012(77) (2012).Google Scholar
Li, Y. K. and Zhao, L. L., ‘Weighted pseudo-almost periodic functions on time scales with applications to cellular neural networks with discrete delays’, Math. Methods Appl. Sci., to appear, 2016, doi:10.1002/mma.4107.Google Scholar
Lizama, C. and Mesquita, J. G., ‘Almost automorphic solutions of dynamic equations on time scales’, J. Funct. Anal. 265 (2013), 2267–2311.CrossRefGoogle Scholar
Lizama, C., Mesquita, J. G. and Ponce, R., ‘A connection between almost periodic functions defined on timescales and ℝ’, Appl. Anal. 93 (2014), 2547–2558.Google Scholar
Wang, C. and Agarwal, R. P., ‘Weighted piecewise pseudo almost automorphic functions with applications to abstract impulsive 𝛻-dynamic equations on time scales’, Adv. Difference Equ. 2014(153) (2014).Google Scholar
Zhang, L. L. and Li, H. X., ‘Weighted pseudo almost periodic solutions for differential equations with piecewise constant arguments’, Bull. Aust. Math. Soc. 92 (2015), 238–250.CrossRefGoogle Scholar