Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T21:57:03.118Z Has data issue: false hasContentIssue false
  • English
  • Français

CONSTRUCTING PERMUTATION POLYNOMIALS OVER FINITE FIELDS

Part of: General field theory Finite fields and commutative rings (number-theoretic aspects)

Published online by Cambridge University Press:  07 August 2013

XIAOER QIN  and
SHAOFANG HONG
XIAOER QIN
Affiliation:
Mathematical College, Sichuan University, Chengdu 610064, PR China email qincn328@sina.com College of Mathematics and Computer Science, Yangtze Normal University, Chongqing 408100, PR China email qincn328@sina.com
SHAOFANG HONG*
Affiliation:
Yangtze Center of Mathematics, Sichuan University, Chengdu 610064, PR China email s-f.hong@tom.com, hongsf02@yahoo.com Mathematical College, Sichuan University, Chengdu 610064, PR China email s-f.hong@tom.com, hongsf02@yahoo.com
*
✉sfhong@scu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we construct several new permutation polynomials over finite fields. First, using the linearised polynomials, we construct the permutation polynomial of the form 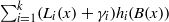${ \mathop{\sum }\nolimits}_{i= 1}^{k} ({L}_{i} (x)+ {\gamma }_{i} ){h}_{i} (B(x))$ over 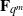${\mathbf{F} }_{{q}^{m} } $, where 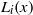${L}_{i} (x)$ and 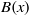$B(x)$ are linearised polynomials. This extends a theorem of Coulter, Henderson and Matthews. Consequently, we generalise a result of Marcos by constructing permutation polynomials of the forms 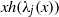$xh({\lambda }_{j} (x))$ and 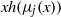$xh({\mu }_{j} (x))$, where 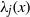${\lambda }_{j} (x)$ is the 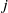$j$th elementary symmetric polynomial of 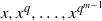$x, {x}^{q} , \ldots , {x}^{{q}^{m- 1} } $ and 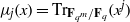${\mu }_{j} (x)= {\mathrm{Tr} }_{{\mathbf{F} }_{{q}^{m} } / {\mathbf{F} }_{q} } ({x}^{j} )$. This answers an open problem raised by Zieve in 2010. Finally, by using the linear translator, we construct the permutation polynomial of the form 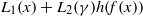${L}_{1} (x)+ {L}_{2} (\gamma )h(f(x))$ over ${\mathbf{F} }_{{q}^{m} } $, which extends a result of Kyureghyan.

Keywords

permutation polynomiallinearised polynomiallinear translatorelementary symmetric polynomial

MSC classification

Secondary: 11T06: Polynomials 12E20: Finite fields (field-theoretic aspects)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 89 , Issue 3 , June 2014 , pp. 420 - 430
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Ayad, M., Belghaba, K. and Kihel, O., ‘On permutation binomials over finite fields’, Bull. Aust. Math. Soc., doi:10.1017/S0004972713000208. Published online March 28, 2013.Google Scholar
Charpin, P. and Kyureghyan, G., ‘When does $F(x)+ \gamma Tr(H(x))$ permute ${F}_{{p}^{n} } $?’, Finite Fields Appl. 15 (2009), 615–632.Google Scholar
Coulter, R., Henderson, M. and Matthews, R., ‘A note on constructing permutation polynomials’, Finite Fields Appl. 15 (2009), 553–557.CrossRefGoogle Scholar
Kyureghyan, G., ‘Constructuring permutations of finite fields via linear translators’, J. Combin. Theory Ser. A 118 (2011), 1052–1061.CrossRefGoogle Scholar
Laigle-Chapuy, Y., ‘Permutation polynomials and applications to coding theory’, Finite Fields Appl. 13 (2007), 58–70.CrossRefGoogle Scholar
Lidl, R. and Mullen, G. L., ‘When does a polynomial over a finite field permute the elements of the field?’, Amer. Math. Monthly 95 (1988), 243–246.Google Scholar
Lidl, R. and Niederreiter, H., Finite Fields, 2nd edn, Encyclopedia of Mathematics and its Applications, 20 (Cambridge University Press, Cambridge, 1997).Google Scholar
Marcos, J. E., ‘Specific permutation polynomials over finite fields’, Finite Fields Appl. 17 (2011), 105–112.CrossRefGoogle Scholar
Masuda, A. and Zieve, M. E., ‘Permutation binomials over finite fields’, Trans. Amer. Math. Soc. 361 (2009), 4169–4180.Google Scholar
Schwenk, J. and Huber, K., ‘Public key encryption and digital signatures based on permutation polynomials’, Electron. Lett. 34 (1998), 759–760.Google Scholar
Wan, D. and Lidl, R., ‘Permutation polynomials of the form ${x}^{r} f({x}^{(q- 1)/ d} )$ and their group structure’, Monatsh. Math. 112 (1991), 149–163.Google Scholar
Zieve, M. E., ‘Some families of permutation polynomials over finite fields’, Int. J. Number Theory 4 (2008), 851–857.CrossRefGoogle Scholar
Zieve, M. E., ‘On some permutation polynomials over ${F}_{q} $ of the form ${x}^{r} h({x}^{(q- 1)/ d} )$’, Proc. Amer. Math. Soc. 137 (2009), 2209–2216.CrossRefGoogle Scholar
Zieve, M. E., ‘Classes of permutation polynomials based on cylotomy and an additive analogue’, in: Additive Number Theory (Springer, 2010), 355–361.CrossRefGoogle Scholar