Published online by Cambridge University Press: 02 November 2016
Because of its practical and theoretical importance in rheology, numerous algorithms have been proposed and utilised to solve the convolution equation 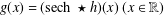 $g(x)=(\text{sech}\,\star h)(x)\;(x\in \mathbb{R})$ for
$g(x)=(\text{sech}\,\star h)(x)\;(x\in \mathbb{R})$ for 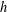 $h$ , given
$h$ , given 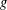 $g$ . There are several approaches involving the use of series expansions of derivatives of
$g$ . There are several approaches involving the use of series expansions of derivatives of 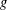 $g$ , which are then truncated to a small number of terms for practical application. Such truncations can only be expected to be valid if the infinite series converge. In this note, we examine two specific truncations and provide a rigorous analysis to obtain sufficient conditions on
$g$ , which are then truncated to a small number of terms for practical application. Such truncations can only be expected to be valid if the infinite series converge. In this note, we examine two specific truncations and provide a rigorous analysis to obtain sufficient conditions on 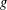 $g$ (and equivalently on
$g$ (and equivalently on 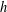 $h$ ) for the convergence of the series concerned.
$h$ ) for the convergence of the series concerned.