No CrossRef data available.
Article contents
Convexité holomorphe intermédiaire des revetements d'un domaine pseudoconvexe
Published online by Cambridge University Press: 17 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let M be a complex manifold and L → M be a positive holomorphic line bundle over M equipped with a Hermitian metric h of class C2. If D ⊂⊂ M is a pseudoconvex domain which is relatively compact in M then there exists an integer r0 such that for every r ≥ r0 and for every connected holomorphic covering π: 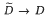 the covering
the covering 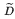 is holomorphically convex with respect to holomorphic sections of
is holomorphically convex with respect to holomorphic sections of 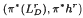 .
.
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 56 , Issue 2 , October 1997 , pp. 285 - 290
- Copyright
- Copyright © Australian Mathematical Society 1997
References
Bibliographie
[1]Asserda, S., ‘The Levi problem on projective manifolds’, Math. Z. 219 (1995), 631–636.CrossRefGoogle Scholar
[2]Demailly, J.P., ‘Estimations L 2 pour l'opérateur ∂ d'un fibré holomorphe semi-positif au dessus d'une variété kähleriénne complète’, Ann. Sci. Écol. Norm. Sup. 15 (1982), 457–511.CrossRefGoogle Scholar
[4]Grauert, H., ‘Bemerkenswerte pseudokonvexe mannifaltigkeiten’, Math. Z. 81 (1963), 377–392.CrossRefGoogle Scholar
[5]Hörmander, L., An introducion to complex analsis in several variables, North-Holland Mathematical Library, (Third Edition – revised), 1990.Google Scholar
[6]Napier, T., ‘Convexity properties of coverings of smooth projective varieties’, Math. Ann. 286 (1990), 433–479.CrossRefGoogle Scholar
[7]Napier, T., ‘Covering spaces of families of compact Riemann surfaces’, Math. Ann. 294 (1992), 523–549.CrossRefGoogle Scholar
[8]Stein, K., ‘Uberlayerungen holomorph-vollstandiger komplexer Râume’, Arch. Math. 7 (1956), 354–361.CrossRefGoogle Scholar


