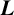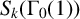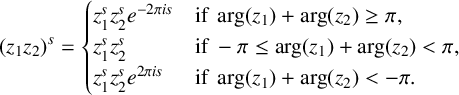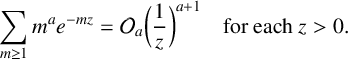1 Introduction
Let
be a normalised cuspidal Hecke eigenform of weight k on
![]() $\Gamma _0(1):=\mathrm {SL}_2(\mathbb {Z})$
. It is well known that its associated L-function
$\Gamma _0(1):=\mathrm {SL}_2(\mathbb {Z})$
. It is well known that its associated L-function
![]() $L(f,s)$
, defined for
$L(f,s)$
, defined for
![]() $ \mathrm {Re}(s)> {(k+1)}/{2}$
by the absolutely convergent series
$ \mathrm {Re}(s)> {(k+1)}/{2}$
by the absolutely convergent series
 $$ \begin{align*} \sum_{n\geq 1} \frac{a_f(n)}{n^s}, \end{align*} $$
$$ \begin{align*} \sum_{n\geq 1} \frac{a_f(n)}{n^s}, \end{align*} $$
can be analytically continued as an entire function for all s. Further, by virtue of the Euler product and functional equation, its nontrivial zeros lie inside the critical strip
![]() $(k-1)/2 < \mathrm {Re}(s) < (k+1)/2$
. The generalised Riemann Hypothesis predicts that they all lie on the critical line
$(k-1)/2 < \mathrm {Re}(s) < (k+1)/2$
. The generalised Riemann Hypothesis predicts that they all lie on the critical line
![]() $\mathrm {Re}(s) = k/2$
.
$\mathrm {Re}(s) = k/2$
.
For even integers
![]() $k \geq 12$
, let
$k \geq 12$
, let
![]() $S_k$
denote the space of cusp forms of weight k and level 1 and let
$S_k$
denote the space of cusp forms of weight k and level 1 and let
![]() $\mathcal {B}_k$
denote the (orthogonal) basis of arithmetically normalised (that is,
$\mathcal {B}_k$
denote the (orthogonal) basis of arithmetically normalised (that is,
![]() $a_f(1)=1$
) Hecke eigenforms in
$a_f(1)=1$
) Hecke eigenforms in
![]() $S_k$
. Given a real number
$S_k$
. Given a real number
![]() $t_0$
and a small positive real number
$t_0$
and a small positive real number
![]() $\delta $
, Kohnen in [Reference Khuri-Makdisi, Kohnen and Raji6] proved the nonvanishing of the sum
$\delta $
, Kohnen in [Reference Khuri-Makdisi, Kohnen and Raji6] proved the nonvanishing of the sum
 $$ \begin{align*}\sum_{f \in \mathcal{B}_k} \frac{L^*(f,s)}{\langle f,f \rangle} \end{align*} $$
$$ \begin{align*}\sum_{f \in \mathcal{B}_k} \frac{L^*(f,s)}{\langle f,f \rangle} \end{align*} $$
for any point s on the line segments
for large enough
![]() $k \gg _{t_0,\delta } 1$
, where
$k \gg _{t_0,\delta } 1$
, where
![]() $L^*(f,s)$
is the completed L-function (defined in Section 2.2). As a corollary, it follows that given such a point s, there is at least one form f in
$L^*(f,s)$
is the completed L-function (defined in Section 2.2). As a corollary, it follows that given such a point s, there is at least one form f in
![]() $\mathcal {B}_k$
such that
$\mathcal {B}_k$
such that
![]() $L(f,s) \neq 0$
for k large. Recently, in [Reference Choie, Kohnen and Zhang2], the authors extended the above results to the simultaneous nonvanishing of L-values (on average) at two points inside the critical strip. More precisely, given positive real numbers T and
$L(f,s) \neq 0$
for k large. Recently, in [Reference Choie, Kohnen and Zhang2], the authors extended the above results to the simultaneous nonvanishing of L-values (on average) at two points inside the critical strip. More precisely, given positive real numbers T and
![]() $\delta $
, they proved the nonvanishing of the sum
$\delta $
, they proved the nonvanishing of the sum
 $$ \begin{align*} \sum_{f \in \mathcal{B}_k} \frac{L^*(f,s_1)L^*(f,s_2)}{\langle f,f \rangle} \end{align*} $$
$$ \begin{align*} \sum_{f \in \mathcal{B}_k} \frac{L^*(f,s_1)L^*(f,s_2)}{\langle f,f \rangle} \end{align*} $$
for large enough
![]() $k \gg _{T,\delta } 1$
when
$k \gg _{T,\delta } 1$
when
![]() $(s_1,s_2) \in R^{\prime }_{T,\delta }$
, where
$(s_1,s_2) \in R^{\prime }_{T,\delta }$
, where
![]() $R^{\prime }_{T,\delta }$
is the set
$R^{\prime }_{T,\delta }$
is the set
Again, as a consequence, they observed that for a given
![]() $(s_1,s_2) \in R^{\prime }_{T,\delta }$
, there exists a Hecke eigenform f in
$(s_1,s_2) \in R^{\prime }_{T,\delta }$
, there exists a Hecke eigenform f in
![]() $S_k$
such that
$S_k$
such that
![]() $L(f,s_1)L(f,s_2) \neq 0$
, when k is sufficiently large.
$L(f,s_1)L(f,s_2) \neq 0$
, when k is sufficiently large.
In this context, it seems natural to ask the following question.
Question 1.1. Given a weight k and complex points
![]() $s,s_1,s_2$
such that
$s,s_1,s_2$
such that
is it possible to quantify the numbers
 $$ \begin{align} \begin{split} N_k(s):=&\;\#\{f\in \mathcal{B}_k~|~L(f,s) \neq 0\},\\ N_k(s_1,s_2):=&\;\#\{f \in \mathcal{B}_k \mid L(f,s_1)\cdot L(f,s_2) \neq 0\}, \end{split} \end{align} $$
$$ \begin{align} \begin{split} N_k(s):=&\;\#\{f\in \mathcal{B}_k~|~L(f,s) \neq 0\},\\ N_k(s_1,s_2):=&\;\#\{f \in \mathcal{B}_k \mid L(f,s_1)\cdot L(f,s_2) \neq 0\}, \end{split} \end{align} $$
in terms of k?
We provide some partial estimates for (1.1). Given an arbitrary positive real number T and small positive reals
![]() $\delta $
and
$\delta $
and
![]() $\delta ^{\prime }$
, we consider the subset of
$\delta ^{\prime }$
, we consider the subset of
![]() ${\mathbb C}^2$
,
${\mathbb C}^2$
,
 $$ \begin{align} R_{T,\delta,\delta^{\prime}} :=&\bigg \{\bigg(s_1=\frac{k}{2}+\epsilon_1+i\beta_1,s_2=\frac{k}{2}+\epsilon_2+i\beta_2\bigg) \in {\mathbb C}^2 \,\bigg| \nonumber \\ & -T \leq \beta_1, \beta_2 \leq T, 0 < |\epsilon_1| < |\epsilon_1|+\delta^{\prime} \leq |\epsilon_2| \leq \frac{1}{2},~|\epsilon_1|+|\epsilon_2| \geq \frac{1}{2}+\delta\bigg \}. \end{align} $$
$$ \begin{align} R_{T,\delta,\delta^{\prime}} :=&\bigg \{\bigg(s_1=\frac{k}{2}+\epsilon_1+i\beta_1,s_2=\frac{k}{2}+\epsilon_2+i\beta_2\bigg) \in {\mathbb C}^2 \,\bigg| \nonumber \\ & -T \leq \beta_1, \beta_2 \leq T, 0 < |\epsilon_1| < |\epsilon_1|+\delta^{\prime} \leq |\epsilon_2| \leq \frac{1}{2},~|\epsilon_1|+|\epsilon_2| \geq \frac{1}{2}+\delta\bigg \}. \end{align} $$
If
![]() $(s_1,s_2) \in R_{T,\delta ,\delta ^{\prime }}$
, we prove the lower bound
$(s_1,s_2) \in R_{T,\delta ,\delta ^{\prime }}$
, we prove the lower bound
when k is sufficiently large,
![]() $k \gg _{T,\delta ,\delta ^{\prime }} 1$
. Here,
$k \gg _{T,\delta ,\delta ^{\prime }} 1$
. Here,
![]() $\delta ^{\prime \prime }$
is an arbitrarily small fixed positive number.
$\delta ^{\prime \prime }$
is an arbitrarily small fixed positive number.
The lower bound for
![]() $N_k(s)$
is obtained as a special case of (1.3). For this, first we consider the strip
$N_k(s)$
is obtained as a special case of (1.3). For this, first we consider the strip
 $$ \begin{align*} S_{T,\delta,\delta^{\prime}} & := \bigg\{-T \leq \mathrm{Im}(s) \leq T, \frac{k-1}{2}+\delta^{\prime} \leq \mathrm{Re}(s) \leq \frac{k}{2} - \delta \bigg\} \\ & \quad \cup \bigg\{-T \leq \mathrm{Im}(s) \leq T, \frac{k}{2} +\delta \leq \mathrm{Re}(s) \leq \frac{k+1}{2} - \delta^{\prime} \bigg\}. \end{align*} $$
$$ \begin{align*} S_{T,\delta,\delta^{\prime}} & := \bigg\{-T \leq \mathrm{Im}(s) \leq T, \frac{k-1}{2}+\delta^{\prime} \leq \mathrm{Re}(s) \leq \frac{k}{2} - \delta \bigg\} \\ & \quad \cup \bigg\{-T \leq \mathrm{Im}(s) \leq T, \frac{k}{2} +\delta \leq \mathrm{Re}(s) \leq \frac{k+1}{2} - \delta^{\prime} \bigg\}. \end{align*} $$
For any
![]() $s \in S_{T,\delta ,\delta ^{\prime }}$
, we obtain the explicit lower bound in terms of the weight k,
$s \in S_{T,\delta ,\delta ^{\prime }}$
, we obtain the explicit lower bound in terms of the weight k,
(see Corollary 3.5 below) for large enough
![]() $k\gg _{T,\delta , \delta ^{\prime }} 1$
.
$k\gg _{T,\delta , \delta ^{\prime }} 1$
.
At the central critical point
![]() $s={k}/{2}$
, Luo [Reference Luo7, formula (4)] showed that for integers k divisible by
$s={k}/{2}$
, Luo [Reference Luo7, formula (4)] showed that for integers k divisible by
![]() $4$
,
$4$
,
![]() $N_k(k/2) \gg k$
as
$N_k(k/2) \gg k$
as
![]() $k \rightarrow \infty $
.
$k \rightarrow \infty $
.
Our bound is of the order
![]() $k^{1/2}$
and so is weaker than this estimate of Luo. However, the method is considerably simpler and does not use the technique of mollified averages as in [Reference Luo7]. Further, we only assume k to be even. As for
$k^{1/2}$
and so is weaker than this estimate of Luo. However, the method is considerably simpler and does not use the technique of mollified averages as in [Reference Luo7]. Further, we only assume k to be even. As for
![]() $N_k(s_1,s_2)$
, currently, it seems that no such estimates are available.
$N_k(s_1,s_2)$
, currently, it seems that no such estimates are available.
1.1 The approach
As in our earlier paper [Reference Manickam, Murty and Sandeep9], we consider a kernel function
![]() $f_{k,s}(z)$
studied by Kohnen [Reference Khuri-Makdisi, Kohnen and Raji6] for suitable s (for its definition see Section 2.3) satisfying
$f_{k,s}(z)$
studied by Kohnen [Reference Khuri-Makdisi, Kohnen and Raji6] for suitable s (for its definition see Section 2.3) satisfying
 $$ \begin{align} f_{k,s}(z) = \text{(constant)}\sum_{f \in \mathcal{B}_k} \dfrac{L^*(f,s)}{\langle f,f \rangle}f(z), \end{align} $$
$$ \begin{align} f_{k,s}(z) = \text{(constant)}\sum_{f \in \mathcal{B}_k} \dfrac{L^*(f,s)}{\langle f,f \rangle}f(z), \end{align} $$
and adapt a method of Rankin and Swinnerton-Dyer [Reference Rankin and Swinnerton-Dyer13] to obtain an explicit expression for
![]() $f_{k,s}(it)$
, valid for all
$f_{k,s}(it)$
, valid for all
![]() $t \geq 1$
, all even
$t \geq 1$
, all even
![]() $k \geq 12$
and any s satisfying
$k \geq 12$
and any s satisfying
![]() ${(k-1)}/{2} \leq \mathrm {Re}(s) \leq {(k+1)}/{2}$
(see Theorem 3.1 below). As a consequence, we are able to provide the following applications.
${(k-1)}/{2} \leq \mathrm {Re}(s) \leq {(k+1)}/{2}$
(see Theorem 3.1 below). As a consequence, we are able to provide the following applications.
1.2 Application 1
Using the above expression for a real parameter
![]() $\sigma $
, we prove that
$\sigma $
, we prove that
![]() $f_{k,\sigma }(ik)>0$
when
$f_{k,\sigma }(ik)>0$
when
![]() $k\gg 1$
and
$k\gg 1$
and
![]() $4\mid k$
. Along with the fact (see Lemma 6.1) that
$4\mid k$
. Along with the fact (see Lemma 6.1) that
![]() $f(ik)>0$
for any normalised Hecke eigenform f of weight k for
$f(ik)>0$
for any normalised Hecke eigenform f of weight k for
![]() $\mathrm {SL}_{2}(\mathbb Z)$
, this proves for a given
$\mathrm {SL}_{2}(\mathbb Z)$
, this proves for a given
![]() $\sigma $
inside the critical strip that there is an f satisfying
$\sigma $
inside the critical strip that there is an f satisfying
![]() $L(f,\sigma )>0$
. This leads us to a small improvement to [Reference Manickam, Murty and Sandeep9, Corollary 2.2.1].
$L(f,\sigma )>0$
. This leads us to a small improvement to [Reference Manickam, Murty and Sandeep9, Corollary 2.2.1].
1.3 Application 2
Let
![]() $T,\delta ,\;\delta ^{\prime }$
be as above. For complex points
$T,\delta ,\;\delta ^{\prime }$
be as above. For complex points
![]() $s_1$
and
$s_1$
and
![]() $s_2$
inside the critical strip such that the pair
$s_2$
inside the critical strip such that the pair
![]() $(s_1,s_2) \in R_{T,\delta ,\delta ^{\prime }}$
, we study the Mellin transform of
$(s_1,s_2) \in R_{T,\delta ,\delta ^{\prime }}$
, we study the Mellin transform of
![]() $f_{k,s_1}$
with respect to
$f_{k,s_1}$
with respect to
![]() $s_2$
by applying a Mellin transform on both sides of (1.5). Then we show (Theorem 3.3) that there is a constant
$s_2$
by applying a Mellin transform on both sides of (1.5). Then we show (Theorem 3.3) that there is a constant
![]() $C=C(T, \delta , \delta ^{\prime })>0$
such that
$C=C(T, \delta , \delta ^{\prime })>0$
such that
for
![]() $k \geq C$
. Here, we are using (1.5) and writing
$k \geq C$
. Here, we are using (1.5) and writing
 $$ \begin{align*}L^*(f_{k,s_1},s_2)\ =\ \text{(constant)}\sum_{f \in \mathcal{B}_k} \dfrac{L^*(f,s_1)}{\langle f,f \rangle}L^*(f,s_2). \end{align*} $$
$$ \begin{align*}L^*(f_{k,s_1},s_2)\ =\ \text{(constant)}\sum_{f \in \mathcal{B}_k} \dfrac{L^*(f,s_1)}{\langle f,f \rangle}L^*(f,s_2). \end{align*} $$
Clearly C is independent of the chosen points
![]() $s_1,s_2$
, and the implicit constant depends only on
$s_1,s_2$
, and the implicit constant depends only on
![]() $T,\delta ^{\prime }$
. Using the lower bound obtained for
$T,\delta ^{\prime }$
. Using the lower bound obtained for
![]() $L^*(f_{k,s_1},s_2)$
in (1.6) for large k, we prove (1.3). Finally, as a corollary, we obtain (1.4). The lower bound (1.4) is meant to illustrate an immediate application of (1.3) and these bounds may be known already.
$L^*(f_{k,s_1},s_2)$
in (1.6) for large k, we prove (1.3). Finally, as a corollary, we obtain (1.4). The lower bound (1.4) is meant to illustrate an immediate application of (1.3) and these bounds may be known already.
In [Reference Sengupta14], the author proves the lower bound
![]() $ N_k(k/2) \gg _{\delta ^{\prime \prime }} k^{1-\delta ^{\prime \prime }} $
when
$ N_k(k/2) \gg _{\delta ^{\prime \prime }} k^{1-\delta ^{\prime \prime }} $
when
![]() $4 \mid k$
, assuming the Lindelöf hypothesis in the k-aspect for
$4 \mid k$
, assuming the Lindelöf hypothesis in the k-aspect for
![]() $L(f,s)$
. The method also involves Kohnen’s kernel function and is related to ours. However, unlike [Reference Choie, Kohnen and Zhang2, Reference Sengupta14], we do not use the explicit expressions for the Fourier coefficients of the respective kernel functions.
$L(f,s)$
. The method also involves Kohnen’s kernel function and is related to ours. However, unlike [Reference Choie, Kohnen and Zhang2, Reference Sengupta14], we do not use the explicit expressions for the Fourier coefficients of the respective kernel functions.
We also mention here that an identity for
![]() $L^*(f_{k,s_1},s_2)$
in terms of ratios of
$L^*(f_{k,s_1},s_2)$
in terms of ratios of
![]() $\Gamma $
functions,
$\Gamma $
functions,
![]() $\zeta $
functions and hypergeometric functions is known [Reference Kohnen5, Theorem 1] when
$\zeta $
functions and hypergeometric functions is known [Reference Kohnen5, Theorem 1] when
![]() $s_1+s_2 \in 2\mathbb {Z}+1 \cap (1,k-1)$
,
$s_1+s_2 \in 2\mathbb {Z}+1 \cap (1,k-1)$
,
![]() $1 < \mathrm {Re}(s_j) < k-1$
and
$1 < \mathrm {Re}(s_j) < k-1$
and
![]() $\mathrm {Re}(s_1)> \mathrm {Re}(s_2) +1$
. The approach in [Reference Kohnen5] is to write the Mellin transform of
$\mathrm {Re}(s_1)> \mathrm {Re}(s_2) +1$
. The approach in [Reference Kohnen5] is to write the Mellin transform of
![]() $f_{k,s_1}$
with respect to
$f_{k,s_1}$
with respect to
![]() $s_2$
as a sum of certain term-wise integrals, obtained by splitting the series
$s_2$
as a sum of certain term-wise integrals, obtained by splitting the series
![]() $f_{k,s_1}$
in a suitable way. We also use similar methods to estimate
$f_{k,s_1}$
in a suitable way. We also use similar methods to estimate
![]() $L^*(f_{k,s_1},s_2)$
, although we cover a wider range of points
$L^*(f_{k,s_1},s_2)$
, although we cover a wider range of points
![]() $s_1,s_2$
within the critical strip. But our main goal is to address the question posed regarding counts which differs from the aim of [Reference Kohnen5].
$s_1,s_2$
within the critical strip. But our main goal is to address the question posed regarding counts which differs from the aim of [Reference Kohnen5].
2 Notations and preliminaries
2.1 Notation
We mention the following asymptotic notation.
-
(1)
 $f(s)={\mathcal O}(g(s)),~s \in S$
, or equivalently,
$f(s)={\mathcal O}(g(s)),~s \in S$
, or equivalently,
 $f(s) \ll g(s),~s \in S$
, means there exists a constant c such that
$f(s) \ll g(s),~s \in S$
, means there exists a constant c such that
 $|f(s)| \leq c|g(s)|$
for all
$|f(s)| \leq c|g(s)|$
for all
 $s\in S$
.
$s\in S$
. -
(2)
 $f(s) \sim g(s),~ s\rightarrow s_0$
, means
$f(s) \sim g(s),~ s\rightarrow s_0$
, means
 $\lim _{s\rightarrow s_0}{f(s)}/t{g(s)} = 1$
.
$\lim _{s\rightarrow s_0}{f(s)}/t{g(s)} = 1$
.
2.2 Preliminaries
Let
![]() $\mathbb {H}$
denote the upper half plane. For
$\mathbb {H}$
denote the upper half plane. For
![]() $z \neq 0$
and
$z \neq 0$
and
![]() $s \in \mathbb {C}$
, we set
$s \in \mathbb {C}$
, we set
![]() $z^s = \exp (s \log z)$
with
$z^s = \exp (s \log z)$
with
![]() $\log z = \log |z| + i \arg z$
, where
$\log z = \log |z| + i \arg z$
, where
![]() $-\pi < \arg z \leq \pi $
. Let
$-\pi < \arg z \leq \pi $
. Let
![]() $k \geq 12$
be a positive even integer and
$k \geq 12$
be a positive even integer and
![]() $z\in \mathbb {H}$
.
$z\in \mathbb {H}$
.
Let
![]() $S_k$
denote the space of cusp forms of weight k with respect to
$S_k$
denote the space of cusp forms of weight k with respect to
![]() $\mathrm {SL}_2(\mathbb {Z})$
. For
$\mathrm {SL}_2(\mathbb {Z})$
. For
![]() $g \in S_k$
, the associated L-series,
$g \in S_k$
, the associated L-series,
 $$ \begin{align*}L(g,s):=\sum_{n \geq 1} \frac{a_g(n)}{n^s},\end{align*} $$
$$ \begin{align*}L(g,s):=\sum_{n \geq 1} \frac{a_g(n)}{n^s},\end{align*} $$
is holomorphic on the half plane
![]() $\mathrm {Re}(s)>{(k+1)}/{2}$
. We define the completed Hecke L-series associated to g as
$\mathrm {Re}(s)>{(k+1)}/{2}$
. We define the completed Hecke L-series associated to g as
which is also equal to the Mellin transform of g, given by
 $$ \begin{align*} \mathcal{M}(g)(s):=\int_{0}^{\infty}g(it)t^{s-1}\,dt. \end{align*} $$
$$ \begin{align*} \mathcal{M}(g)(s):=\int_{0}^{\infty}g(it)t^{s-1}\,dt. \end{align*} $$
Since
![]() $\mathcal {M}(g)(s)$
is known to be entire,
$\mathcal {M}(g)(s)$
is known to be entire,
![]() $L^*(g,s)$
(and also
$L^*(g,s)$
(and also
![]() $L(g,s)$
) can be uniquely extended as an entire function. Moreover,
$L(g,s)$
) can be uniquely extended as an entire function. Moreover,
![]() $L^*(g,s)$
satisfies the functional equation
$L^*(g,s)$
satisfies the functional equation
For a normalised Hecke eigenform f in
![]() $S_k$
, we define the symmetric square L-function of f by the formula
$S_k$
, we define the symmetric square L-function of f by the formula
 $$ \begin{align*} L(\text{Sym}^2(f),s):=\prod_{p} \frac{1}{(1-\alpha_p^2p^{-s})(1-\alpha_p\beta_pp^{-s})(1-\beta_p^2p^{-s})}, \end{align*} $$
$$ \begin{align*} L(\text{Sym}^2(f),s):=\prod_{p} \frac{1}{(1-\alpha_p^2p^{-s})(1-\alpha_p\beta_pp^{-s})(1-\beta_p^2p^{-s})}, \end{align*} $$
for
![]() $\mathrm {Re}(s)>k$
, where
$\mathrm {Re}(s)>k$
, where
![]() $\alpha _p$
and
$\alpha _p$
and
![]() $\beta _p$
are the roots of the polynomial
$\beta _p$
are the roots of the polynomial
![]() $X^2-a_f(p)X+p^{k-1}$
. The function
$X^2-a_f(p)X+p^{k-1}$
. The function
![]() $L(\text {Sym}^2(f),s)$
extends to an entire function [Reference Shimura15] which is invariant under the map
$L(\text {Sym}^2(f),s)$
extends to an entire function [Reference Shimura15] which is invariant under the map
![]() $s\mapsto 2k-1-s$
.
$s\mapsto 2k-1-s$
.
For
![]() $x,y\in \mathbb {C}$
and
$x,y\in \mathbb {C}$
and
![]() $\mathrm {Re}(x),\mathrm {Re}(y)>0,$
we have the beta function
$\mathrm {Re}(x),\mathrm {Re}(y)>0,$
we have the beta function
 $$ \begin{align*} B(x,y) := \int_{0}^{1} t^{x-1}(1-t)^{y-1} \,dt \end{align*} $$
$$ \begin{align*} B(x,y) := \int_{0}^{1} t^{x-1}(1-t)^{y-1} \,dt \end{align*} $$
and we recall that it satisfies
 $$ \begin{align} B(x,y) &= \frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}= 2\int_{0}^{\pi/2} (\sin \theta)^{2x-1}(\cos \theta)^{2y-1} \,d\theta. \end{align} $$
$$ \begin{align} B(x,y) &= \frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}= 2\int_{0}^{\pi/2} (\sin \theta)^{2x-1}(\cos \theta)^{2y-1} \,d\theta. \end{align} $$
2.3 Kohnen’s cusp form
Let
![]() $s\in {\mathbb C}$
with
$s\in {\mathbb C}$
with
![]() $1<\mathrm {Re}(s)<k-1$
. The kernel function
$1<\mathrm {Re}(s)<k-1$
. The kernel function
![]() $R_{k,s}(z)$
, introduced by Kohnen [Reference Khuri-Makdisi, Kohnen and Raji6], is defined by
$R_{k,s}(z)$
, introduced by Kohnen [Reference Khuri-Makdisi, Kohnen and Raji6], is defined by
 $$ \begin{align} R_{k,s}(z) := \gamma_{k}(s) {\sum}^{\prime} z^{-s}\bigg\vert_{k} \begin{pmatrix} a & b \\ c & d \end{pmatrix}. \end{align} $$
$$ \begin{align} R_{k,s}(z) := \gamma_{k}(s) {\sum}^{\prime} z^{-s}\bigg\vert_{k} \begin{pmatrix} a & b \\ c & d \end{pmatrix}. \end{align} $$
Here
![]() $\vert _{k}$
denotes the standard weight k (integer) action of
$\vert _{k}$
denotes the standard weight k (integer) action of
![]() $\mathrm {GL}_2^+({\mathbb Q})$
on the functions
$\mathrm {GL}_2^+({\mathbb Q})$
on the functions
![]() $g:\mathbb {H} \rightarrow \mathbb {C}$
, defined by
$g:\mathbb {H} \rightarrow \mathbb {C}$
, defined by
 $$ \begin{align*} (g\vert_{k}\gamma)(\tau) := (ad-bc)^{k/2} (c\tau +d)^{-k} g\bigg(\dfrac{a\tau +b}{c\tau + d}\bigg), \quad \tau \in \mathbb{H}, \gamma = \begin{pmatrix} a&b\\c&d \end{pmatrix} \in GL_2^+(\mathbb{Q}), \end{align*} $$
$$ \begin{align*} (g\vert_{k}\gamma)(\tau) := (ad-bc)^{k/2} (c\tau +d)^{-k} g\bigg(\dfrac{a\tau +b}{c\tau + d}\bigg), \quad \tau \in \mathbb{H}, \gamma = \begin{pmatrix} a&b\\c&d \end{pmatrix} \in GL_2^+(\mathbb{Q}), \end{align*} $$
and the sum
![]() $\sum ^\prime $
is taken over all matrices
$\sum ^\prime $
is taken over all matrices
![]() $(\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}) \in \mathrm {SL}_2(\mathbb {Z})$
. Moreover,
$(\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}) \in \mathrm {SL}_2(\mathbb {Z})$
. Moreover,
The function
![]() $R_{k,s}(z)$
is a cusp form of weight k for the full modular group
$R_{k,s}(z)$
is a cusp form of weight k for the full modular group
![]() $\mathrm {SL}_2(\mathbb {Z})$
. If
$\mathrm {SL}_2(\mathbb {Z})$
. If
![]() $\langle \,,\rangle $
denotes the usual Petersson inner product on
$\langle \,,\rangle $
denotes the usual Petersson inner product on
![]() $S_k$
, then the essential property of
$S_k$
, then the essential property of
![]() $R_{k,s}$
is that for any
$R_{k,s}$
is that for any
![]() $g \in S_k$
, by [Reference Khuri-Makdisi, Kohnen and Raji6, Lemma 1],
$g \in S_k$
, by [Reference Khuri-Makdisi, Kohnen and Raji6, Lemma 1],
3 Statement of results
For
![]() $1<\sigma :=\mathrm {Re}(s)<k-1$
and
$1<\sigma :=\mathrm {Re}(s)<k-1$
and
![]() $z \in \mathbb {H}$
, we define
$z \in \mathbb {H}$
, we define
 $$ \begin{align} f_{k,s}(z):= 2 \dfrac{R_{k,s}(z)}{\Gamma(s)\Gamma(k-s)} = e^{i{\pi s}/{2}} {\sum}^{\prime} z^{-s}\bigg\vert_{k} \begin{pmatrix} a & b \\ c & d \end{pmatrix}. \end{align} $$
$$ \begin{align} f_{k,s}(z):= 2 \dfrac{R_{k,s}(z)}{\Gamma(s)\Gamma(k-s)} = e^{i{\pi s}/{2}} {\sum}^{\prime} z^{-s}\bigg\vert_{k} \begin{pmatrix} a & b \\ c & d \end{pmatrix}. \end{align} $$
It follows from (2.1) and (3.1) that
Let
![]() $k\geq 12,~2 \mid k$
and
$k\geq 12,~2 \mid k$
and
![]() $k \not =14$
throughout, unless further conditions are specified.
$k \not =14$
throughout, unless further conditions are specified.
3.1 Asymptotics of
 $f_{k,s}(z)$
on the imaginary axis
$f_{k,s}(z)$
on the imaginary axis
In [Reference Manickam, Murty and Sandeep9, Theorem 2.1], it was shown that for
![]() $\sigma \in [(k-1)/2, (k+1)/2)$
,
$\sigma \in [(k-1)/2, (k+1)/2)$
,
Moreover, [Reference Manickam, Murty and Sandeep9, Theorem 2.2] made explicit the constant implied in the
![]() ${\mathcal O}$
-term and (for
${\mathcal O}$
-term and (for
![]() $4\mid k$
) deduced a lower bound for
$4\mid k$
) deduced a lower bound for
![]() $f_{k,\sigma }(i)$
and from there the lower bound [Reference Manickam, Murty and Sandeep9, Corollary 2.2.1]
$f_{k,\sigma }(i)$
and from there the lower bound [Reference Manickam, Murty and Sandeep9, Corollary 2.2.1]
for any
![]() $\delta> 0$
. Our first result extends (3.3) by replacing
$\delta> 0$
. Our first result extends (3.3) by replacing
![]() $\sigma $
with a complex value of s, and
$\sigma $
with a complex value of s, and
![]() $z=i$
by a general point
$z=i$
by a general point
![]() $z = it$
on the imaginary axis.
$z = it$
on the imaginary axis.
Theorem 3.1. Let
![]() $s=\sigma +i\beta $
be a complex number such that
$s=\sigma +i\beta $
be a complex number such that
![]() ${(k-1)}/{2} \leq \sigma \leq {(k+1)}/{2}$
. Then, for a given
${(k-1)}/{2} \leq \sigma \leq {(k+1)}/{2}$
. Then, for a given
![]() $t\geq 1$
, the cusp form
$t\geq 1$
, the cusp form
![]() $f_{k,s}(it)$
satisfies
$f_{k,s}(it)$
satisfies
 $$ \begin{align*} \bigg|f_{k,s}(it) - \bigg(2\frac{(2\pi)^{s}}{\Gamma(s)}\sum_{n \geq 1} n^{s-1}e^{-2\pi nt} + (-1)^{k/2}2\frac{(2\pi)^{k-s}}{\Gamma(k-s)}\sum_{n \geq 1} n^{k-s-1}e^{-2\pi nt}\bigg) \bigg| \leq \frac{300e^{\pi|\beta|/2}}{t^{k-2}}. \end{align*} $$
$$ \begin{align*} \bigg|f_{k,s}(it) - \bigg(2\frac{(2\pi)^{s}}{\Gamma(s)}\sum_{n \geq 1} n^{s-1}e^{-2\pi nt} + (-1)^{k/2}2\frac{(2\pi)^{k-s}}{\Gamma(k-s)}\sum_{n \geq 1} n^{k-s-1}e^{-2\pi nt}\bigg) \bigg| \leq \frac{300e^{\pi|\beta|/2}}{t^{k-2}}. \end{align*} $$
As a consequence of this result, we show that in fact
![]() $\max _{f \in \mathcal {B}_k} L(f,\sigma )$
is a positive quantity and satisfies the following lower bound.
$\max _{f \in \mathcal {B}_k} L(f,\sigma )$
is a positive quantity and satisfies the following lower bound.
Corollary 3.2. Let
![]() $4\mid k$
and
$4\mid k$
and
![]() $({k-1})/{2} \leq \sigma = ({k}/{2})+\epsilon \leq ({k+1})/{2}$
. For k large enough, there is a Hecke eigenform f in
$({k-1})/{2} \leq \sigma = ({k}/{2})+\epsilon \leq ({k+1})/{2}$
. For k large enough, there is a Hecke eigenform f in
![]() $S_k$
such that
$S_k$
such that
![]() $L(f,\sigma )> 0$
. In particular, for any arbitrarily small
$L(f,\sigma )> 0$
. In particular, for any arbitrarily small
![]() $ \delta ^{\prime }>0$
and large enough
$ \delta ^{\prime }>0$
and large enough
![]() $k \gg _{\delta ^{\prime }} 1$
, we have
$k \gg _{\delta ^{\prime }} 1$
, we have
3.2 Simultaneous nonvanishing
In the next result, we replace
![]() $\sigma $
by a complex point. For this purpose, let us set
$\sigma $
by a complex point. For this purpose, let us set
 $$ \begin{align*}L^*(f_{k,s},w)\ =\ \frac{(-1)^{k/2}\pi \Gamma(k-1)}{2^{k-3}\Gamma(s)\Gamma(k-s)}\sum_{f \in {\mathcal B}_k} \frac{1}{\langle f,f \rangle}L^*(f,s)L^*(f,w). \end{align*} $$
$$ \begin{align*}L^*(f_{k,s},w)\ =\ \frac{(-1)^{k/2}\pi \Gamma(k-1)}{2^{k-3}\Gamma(s)\Gamma(k-s)}\sum_{f \in {\mathcal B}_k} \frac{1}{\langle f,f \rangle}L^*(f,s)L^*(f,w). \end{align*} $$
Theorem 3.3. Let
![]() $T,\delta ,\delta ^{\prime }$
be arbitrary but fixed positive real numbers such that
$T,\delta ,\delta ^{\prime }$
be arbitrary but fixed positive real numbers such that
![]() $0<\delta, \delta ^{\prime } \leq 1/2$
. Let
$0<\delta, \delta ^{\prime } \leq 1/2$
. Let
![]() $(s_1=({k}/{2})+\epsilon _1+i\beta _1,~s_2=({k}/{2})+\epsilon _2+i\beta _2)~\in ~R_{T,\delta ,\delta ^{\prime }}$
. Then there exists a constant
$(s_1=({k}/{2})+\epsilon _1+i\beta _1,~s_2=({k}/{2})+\epsilon _2+i\beta _2)~\in ~R_{T,\delta ,\delta ^{\prime }}$
. Then there exists a constant
![]() $C=C(T,\delta ,\delta ^{\prime })>0$
depending only on
$C=C(T,\delta ,\delta ^{\prime })>0$
depending only on
![]() $T, \delta ,\delta ^{\prime }$
such that
$T, \delta ,\delta ^{\prime }$
such that
In Figure 1, we illustrate the real points in
![]() $R_{T,\delta ,\delta ^{\prime }}$
with
$R_{T,\delta ,\delta ^{\prime }}$
with
![]() $\delta = \delta ^{\prime } = 0.05$
. Combining Theorem 3.3 with a straightforward estimate (see Section 8), we deduce the following result about simultaneous nonvanishing at two points.
$\delta = \delta ^{\prime } = 0.05$
. Combining Theorem 3.3 with a straightforward estimate (see Section 8), we deduce the following result about simultaneous nonvanishing at two points.

Figure 1
![]() $\delta = {0.05}$
,
$\delta = {0.05}$
,
![]() $\delta ^{\prime } = {0.05}$
.
$\delta ^{\prime } = {0.05}$
.
Corollary 3.4. Let
![]() $T,\delta ,\delta ^{\prime },\delta ^{\prime \prime }$
be arbitrary but fixed positive real numbers with
$T,\delta ,\delta ^{\prime },\delta ^{\prime \prime }$
be arbitrary but fixed positive real numbers with
![]() $0<\delta ,\delta ^{\prime } \leq 1/2$
. Let
$0<\delta ,\delta ^{\prime } \leq 1/2$
. Let
![]() $(s_1,s_2) \in R_{T,\delta ,\delta ^{\prime }}$
. Then, for
$(s_1,s_2) \in R_{T,\delta ,\delta ^{\prime }}$
. Then, for
![]() $k \geq C(T,\delta ,\delta ^{\prime })$
,
$k \geq C(T,\delta ,\delta ^{\prime })$
,
We remark here that since
![]() $N_k(s_1,s_2) = N_k(s_2,s_1)$
, it suffices to assume that either
$N_k(s_1,s_2) = N_k(s_2,s_1)$
, it suffices to assume that either
![]() $(s_1,s_2)$
or
$(s_1,s_2)$
or
![]() $(s_2,s_1) \in R_{T,\delta ,\delta ^{\prime }}.$
It should also be noted that Corollary 3.4 does not imply [Reference Choie, Kohnen and Zhang2, Corollary 3.2] since the region
$(s_2,s_1) \in R_{T,\delta ,\delta ^{\prime }}.$
It should also be noted that Corollary 3.4 does not imply [Reference Choie, Kohnen and Zhang2, Corollary 3.2] since the region
![]() $R_{T,\delta ,\delta ^{\prime }}$
that we are considering is a proper subset of
$R_{T,\delta ,\delta ^{\prime }}$
that we are considering is a proper subset of
![]() $R^{\prime }_{T,\delta }$
(except for points
$R^{\prime }_{T,\delta }$
(except for points
![]() $(s_1,s_2)$
in
$(s_1,s_2)$
in
![]() $R_{T,\delta ,\delta ^{\prime }}$
with
$R_{T,\delta ,\delta ^{\prime }}$
with
![]() $\mathrm {Re}(s_2)={(k+1)}/{2}$
).
$\mathrm {Re}(s_2)={(k+1)}/{2}$
).
Now, as a corollary to Corollary 3.4, we obtain an asymptotic lower bound for
![]() $N_k(s_1)$
in terms of k.
$N_k(s_1)$
in terms of k.
Corollary 3.5. Let T be an arbitrary but fixed positive real number and let
![]() $\delta ,\delta ^{\prime },\delta ^{\prime \prime }$
be arbitrary small but fixed positive reals with
$\delta ,\delta ^{\prime },\delta ^{\prime \prime }$
be arbitrary small but fixed positive reals with
![]() $0<\delta ,\delta ^{\prime } \leq 1/2$
. Let
$0<\delta ,\delta ^{\prime } \leq 1/2$
. Let
![]() $s_1=({k}/{2})+\epsilon _1+i\beta _1$
satisfy
$s_1=({k}/{2})+\epsilon _1+i\beta _1$
satisfy
![]() $|\beta _1| \leq T$
and
$|\beta _1| \leq T$
and
![]() $\delta \leq |\epsilon _1| \leq \tfrac 12-\delta ^{\prime }$
. Then, for
$\delta \leq |\epsilon _1| \leq \tfrac 12-\delta ^{\prime }$
. Then, for
![]() $k \ge C(T,\delta,\delta^{\prime})$
,
$k \ge C(T,\delta,\delta^{\prime})$
,
4 Lemmas
We recall some preliminary lemmas which will be useful in the proofs of the results.
Lemma 4.1.
-
(a) For
 $z_1,z_2,s \in \mathbb {C}$
,
$z_1,z_2,s \in \mathbb {C}$
,  $$ \begin{align*} (z_1z_2)^s = \begin{cases} z_1^s z_2^s e^{-2\pi is}\quad &\text{if }\arg(z_1)+\arg(z_2) \geq \pi,\\ z_1^s z_2^s \quad &\text{if } -\pi \leq \arg(z_1)+\arg(z_2) < \pi,\\ z_1^s z_2^s e^{2\pi is}\quad &\text{if }\arg(z_1)+\arg(z_2) < -\pi. \end{cases} \end{align*} $$
$$ \begin{align*} (z_1z_2)^s = \begin{cases} z_1^s z_2^s e^{-2\pi is}\quad &\text{if }\arg(z_1)+\arg(z_2) \geq \pi,\\ z_1^s z_2^s \quad &\text{if } -\pi \leq \arg(z_1)+\arg(z_2) < \pi,\\ z_1^s z_2^s e^{2\pi is}\quad &\text{if }\arg(z_1)+\arg(z_2) < -\pi. \end{cases} \end{align*} $$
-
(b) If
 $z,s=\sigma +i\beta \in \mathbb {C}$
, then
$z,s=\sigma +i\beta \in \mathbb {C}$
, then
 $|z^s|=|z|^{\sigma }e^{-\beta \arg (z)}$
.
$|z^s|=|z|^{\sigma }e^{-\beta \arg (z)}$
.
Proof. The proof is straightforward and follows from the definitions of
![]() $\log $
and
$\log $
and
![]() $\arg $
. Note that
$\arg $
. Note that
![]() $\arg (z)$
denotes the principal argument of z as defined in Section 2.2.
$\arg (z)$
denotes the principal argument of z as defined in Section 2.2.
Lemma 4.2 ([Reference Gautschi4], Gautschi’s inequality)
For
![]() $x>0$
and
$x>0$
and
![]() $s \in (0,1)$
,
$s \in (0,1)$
,
Lemma 4.3 [Reference Abramowitz and Stegun1]
-
(a) For
 $a, b \in \mathbb {C}$
, as
$a, b \in \mathbb {C}$
, as $$ \begin{align*} \dfrac{\Gamma(z+a)}{\Gamma(z+b)} \sim z^{a-b} \end{align*} $$
$$ \begin{align*} \dfrac{\Gamma(z+a)}{\Gamma(z+b)} \sim z^{a-b} \end{align*} $$
 $z \rightarrow \infty $
, along any curve joining
$z \rightarrow \infty $
, along any curve joining
 $0$
and
$0$
and
 $\infty $
, provided
$\infty $
, provided
 $z \notin -a-\mathbb {N} \cup -b-\mathbb {N}$
.
$z \notin -a-\mathbb {N} \cup -b-\mathbb {N}$
.
-
(b) (Real Stirling’s formula). As
 $x\rightarrow \infty $
, we have
$x\rightarrow \infty $
, we have  $$ \begin{align*} \Gamma(x) \sim \bigg(\frac{x}{e}\bigg)^x\sqrt{\frac{2\pi}{x}}. \end{align*} $$
$$ \begin{align*} \Gamma(x) \sim \bigg(\frac{x}{e}\bigg)^x\sqrt{\frac{2\pi}{x}}. \end{align*} $$
-
(c) [Reference Olver, Lozier, Boisvert and Clark11]. We have
(4.1) $$ \begin{align} |\Gamma(x+iy)| \geq (\cosh{\pi y} )^{-{1}/{2}} \Gamma(x),~ x \geq \tfrac{1}{2}, \quad y \in \mathbb{R}. \end{align} $$
$$ \begin{align} |\Gamma(x+iy)| \geq (\cosh{\pi y} )^{-{1}/{2}} \Gamma(x),~ x \geq \tfrac{1}{2}, \quad y \in \mathbb{R}. \end{align} $$
Proof. Part (a) follows from the asymptotic expansion
 $$ \begin{align*} z^{b-a}\frac{\Gamma(z+a)}{\Gamma(z+b)} \sim\! 1\!+ \frac{(a-b)(a+b-1)}{2}\frac{1}{z}\hspace{-0.5pt}+\hspace{-0.5pt}\frac{1}{12}\binom{a-b}{2}(3(a+b-1)^2\hspace{-0.5pt}-\hspace{-0.5pt}a+b-1)\frac{1}{z^2}\hspace{-0.5pt}+\hspace{-0.5pt}\cdots \end{align*} $$
$$ \begin{align*} z^{b-a}\frac{\Gamma(z+a)}{\Gamma(z+b)} \sim\! 1\!+ \frac{(a-b)(a+b-1)}{2}\frac{1}{z}\hspace{-0.5pt}+\hspace{-0.5pt}\frac{1}{12}\binom{a-b}{2}(3(a+b-1)^2\hspace{-0.5pt}-\hspace{-0.5pt}a+b-1)\frac{1}{z^2}\hspace{-0.5pt}+\hspace{-0.5pt}\cdots \end{align*} $$
(see [Reference Abramowitz and Stegun1, 6.1.47 on page 257]) valid for z as above. Part (b) is well known. For part (c), we refer to [Reference Olver, Lozier, Boisvert and Clark11, 5.6.7 on page 138].
Lemma 4.4.
-
(a) For any fixed
 $a> 0$
,
$a> 0$
,  $$ \begin{align*} \sum_{m\geq 1} m^a e^{-mz} = {\mathcal O}_a\bigg(\frac{1}{z}\bigg)^{a+1} \quad\text{for each }z> 0. \end{align*} $$
$$ \begin{align*} \sum_{m\geq 1} m^a e^{-mz} = {\mathcal O}_a\bigg(\frac{1}{z}\bigg)^{a+1} \quad\text{for each }z> 0. \end{align*} $$
-
(b)
 $$ \begin{align*} \max_{z> 0} z^{a+1} \sum_{m \geq 1} m^a e^{-mz} \ll \bigg(\frac{a+1}{e}\bigg)^{a+1}\quad (a\rightarrow \infty). \end{align*} $$
$$ \begin{align*} \max_{z> 0} z^{a+1} \sum_{m \geq 1} m^a e^{-mz} \ll \bigg(\frac{a+1}{e}\bigg)^{a+1}\quad (a\rightarrow \infty). \end{align*} $$
Proof. We refer to [Reference Cohen and Strömberg3, Lemma 9.3.13] for part (a) and [Reference Manickam, Murty and Sandeep9, Lemma 6.1] for part (b).
Lemma 4.5. For
![]() $\sigma \geq 3$
and
$\sigma \geq 3$
and
![]() $\mathrm {Im}(z)=y\geq 1$
,
$\mathrm {Im}(z)=y\geq 1$
,
 $$ \begin{align} \sum_{n \in \mathbb{Z}}\frac{1}{|z+n|^{\sigma}} < \ \frac{7}{y^{\sigma-1}}. \end{align} $$
$$ \begin{align} \sum_{n \in \mathbb{Z}}\frac{1}{|z+n|^{\sigma}} < \ \frac{7}{y^{\sigma-1}}. \end{align} $$
Proof. From [Reference Cohen and Strömberg3, Lemma 3.5.9],
 $$ \begin{align*} \sum_{n \in \mathbb{Z}}\frac{1}{|z+n|^{\sigma}} \leq \frac{1}{y^{\sigma}} +\frac{4}{y^{\sigma-1}}\int_{0}^{\infty}\frac{1}{(u^2+1)^{\sigma/2}} \,du. \end{align*} $$
$$ \begin{align*} \sum_{n \in \mathbb{Z}}\frac{1}{|z+n|^{\sigma}} \leq \frac{1}{y^{\sigma}} +\frac{4}{y^{\sigma-1}}\int_{0}^{\infty}\frac{1}{(u^2+1)^{\sigma/2}} \,du. \end{align*} $$
We estimate this explicitly when
![]() $y \geq 1$
and
$y \geq 1$
and
![]() $\sigma \geq 3$
, using (2.2) and Lemma 4.2:
$\sigma \geq 3$
, using (2.2) and Lemma 4.2:
 $$ \begin{align*} \int_{0}^{\infty}\frac{1}{(u^2+1)^{\sigma/2}} \,du = \int_{0}^{\pi/2} (\cos \theta)^{\sigma-2} \,d\theta = \frac{\Gamma({1}/{2})}{2}\frac{\Gamma((\sigma-1)/2)}{\Gamma(\sigma/2)} \leq \sqrt{\frac{\pi}{2(\sigma-2)}}. \end{align*} $$
$$ \begin{align*} \int_{0}^{\infty}\frac{1}{(u^2+1)^{\sigma/2}} \,du = \int_{0}^{\pi/2} (\cos \theta)^{\sigma-2} \,d\theta = \frac{\Gamma({1}/{2})}{2}\frac{\Gamma((\sigma-1)/2)}{\Gamma(\sigma/2)} \leq \sqrt{\frac{\pi}{2(\sigma-2)}}. \end{align*} $$
Note here that
![]() $\Gamma (1/2) = \sqrt {\pi }$
. It follows that
$\Gamma (1/2) = \sqrt {\pi }$
. It follows that
 $$ \begin{align*} \sum_{n \in \mathbb{Z}}\frac{1}{|z+n|^{\sigma}} \leq \frac{1}{y^{\sigma}} +\frac{4}{y^{\sigma-1}} \sqrt{\frac{\pi}{2(\sigma-2)}} < \frac{7}{y^{\sigma-1}}.\\[-3.5pc] \end{align*} $$
$$ \begin{align*} \sum_{n \in \mathbb{Z}}\frac{1}{|z+n|^{\sigma}} \leq \frac{1}{y^{\sigma}} +\frac{4}{y^{\sigma-1}} \sqrt{\frac{\pi}{2(\sigma-2)}} < \frac{7}{y^{\sigma-1}}.\\[-3.5pc] \end{align*} $$
Finally, we mention an estimate for
![]() $\zeta (s)$
which is valid on
$\zeta (s)$
which is valid on
![]() $\mathrm {Re}(s)>1$
.
$\mathrm {Re}(s)>1$
.
Lemma 4.6. For
![]() $s=\sigma +it$
, where
$s=\sigma +it$
, where
![]() $\sigma>1$
,
$\sigma>1$
,
 $$ \begin{align*} |\zeta(s)|\geq \bigg|\dfrac{\zeta(2\sigma)}{\zeta(\sigma)}\bigg|. \end{align*} $$
$$ \begin{align*} |\zeta(s)|\geq \bigg|\dfrac{\zeta(2\sigma)}{\zeta(\sigma)}\bigg|. \end{align*} $$
Proof. For
![]() $\mathrm {Re}(s)>1$
,
$\mathrm {Re}(s)>1$
,
 $$ \begin{align*} \sum_{n \geq 1} \frac{1}{n^s} = \prod_{p \in \mathcal{P}} \dfrac{1}{1-p^{-s}} \end{align*} $$
$$ \begin{align*} \sum_{n \geq 1} \frac{1}{n^s} = \prod_{p \in \mathcal{P}} \dfrac{1}{1-p^{-s}} \end{align*} $$
where
![]() $\mathcal {P}$
denotes the set of primes. From this and the fact that
$\mathcal {P}$
denotes the set of primes. From this and the fact that
![]() $|p^s -1| \leq p^\sigma +1$
,
$|p^s -1| \leq p^\sigma +1$
,
 $$ \begin{align*} \bigg|\dfrac{\zeta(2\sigma)}{\zeta(\sigma)\zeta(s)}\bigg| = \bigg|\prod_{p \in \mathcal{P}} \dfrac{p^{2\sigma}(p^{\sigma}-1)(p^s-1)}{(p^{2\sigma}-1)p^{\sigma}p^s}\bigg| \leq 1.\\[-3.7pc] \end{align*} $$
$$ \begin{align*} \bigg|\dfrac{\zeta(2\sigma)}{\zeta(\sigma)\zeta(s)}\bigg| = \bigg|\prod_{p \in \mathcal{P}} \dfrac{p^{2\sigma}(p^{\sigma}-1)(p^s-1)}{(p^{2\sigma}-1)p^{\sigma}p^s}\bigg| \leq 1.\\[-3.7pc] \end{align*} $$
5 Proof of Theorem 3.1
Except in the proof of Corollary 3.2, we only assume
![]() $k \geq 12$
and
$k \geq 12$
and
![]() $2 \mid k$
.
$2 \mid k$
.
Proof of Theorem 3.1
The series for
![]() $R_{k,s}(z)$
in (2.3) runs over a set of integral matrices with determinant
$R_{k,s}(z)$
in (2.3) runs over a set of integral matrices with determinant
![]() $1$
. As we have absolute convergence for z with positive imaginary part, we can rearrange this series in terms of the sum of the squares of the entries along each row (of the matrix) to get
$1$
. As we have absolute convergence for z with positive imaginary part, we can rearrange this series in terms of the sum of the squares of the entries along each row (of the matrix) to get
 $$ \begin{align} e^{i{\pi}s/{2}} \displaystyle\sum_{\substack{M\geq 1\\N\geq 1}} \displaystyle\sum_{a^2+b^2 = \boldsymbol{M}} \displaystyle\sum_{\substack{c^2+d^2 = \boldsymbol{N}\\ \det \big(\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big) = 1}} (cz+d)^{-k}\bigg(\dfrac{az+b}{cz+d}\bigg)^{-s}. \end{align} $$
$$ \begin{align} e^{i{\pi}s/{2}} \displaystyle\sum_{\substack{M\geq 1\\N\geq 1}} \displaystyle\sum_{a^2+b^2 = \boldsymbol{M}} \displaystyle\sum_{\substack{c^2+d^2 = \boldsymbol{N}\\ \det \big(\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big) = 1}} (cz+d)^{-k}\bigg(\dfrac{az+b}{cz+d}\bigg)^{-s}. \end{align} $$
For
![]() $ M_0, N_0 \in \mathbb {N}$
, we define
$ M_0, N_0 \in \mathbb {N}$
, we define
 $$ \begin{align*} T_{\boldsymbol{M}_0,\boldsymbol{N}_0,s}(z) &:= \, e^{i{\pi}s/{2}} \displaystyle\sum_{a^2+b^2 = \boldsymbol{M}_0} \displaystyle\sum_{\substack{c^2+d^2 = \boldsymbol{N}_0\\ \det \big(\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big) = 1}} (cz+d)^{-k}\bigg(\dfrac{az+b}{cz+d}\bigg)^{-s}, \\T_{\boldsymbol{M}_0,\geq\boldsymbol{N}_0,s}(z) &:= \, e^{i{\pi}s/{2}} \displaystyle\sum_{a^2+b^2 = \boldsymbol{M}_0} \displaystyle\sum_{N \in \mathbb{Z} \atop N\geq \boldsymbol{N}_0} \displaystyle\sum_{\substack{c^2+d^2 = N\\ \det \big(\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big) = 1}}(cz+d)^{-k}\bigg(\dfrac{az+b}{cz+d}\bigg)^{-s},\\ T_{\geq \boldsymbol{M}_0,\boldsymbol{N}_0,s}(z) &:= \, e^{i{\pi}s/{2}} \displaystyle\sum_{M \in \mathbb{Z} \atop M \geq \boldsymbol{M}_0} \displaystyle\sum_{a^2+b^2 = M} \displaystyle\sum_{\substack{c^2+d^2 = \boldsymbol{N}_0\\ \det \big(\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big) = 1}}(cz+d)^{-k}\bigg(\dfrac{az+b}{cz+d}\bigg)^{-s}, \\T_{\geq \boldsymbol{M}_0,\geq \boldsymbol{N}_0,s}(z) &:= \, e^{i{\pi}s/{2}} \displaystyle\sum_{M \in \mathbb{Z} \atop M \geq \boldsymbol{M}_0} \displaystyle\sum_{a^2+b^2 = M} \displaystyle\sum_{N \in \mathbb{Z} \atop N \geq \boldsymbol{N}_0} \displaystyle\sum_{\substack{c^2+d^2 = N\\ \det \big(\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big) = 1}}(cz+d)^{-k}\bigg(\dfrac{az+b}{cz+d}\bigg)^{-s}, \end{align*} $$
$$ \begin{align*} T_{\boldsymbol{M}_0,\boldsymbol{N}_0,s}(z) &:= \, e^{i{\pi}s/{2}} \displaystyle\sum_{a^2+b^2 = \boldsymbol{M}_0} \displaystyle\sum_{\substack{c^2+d^2 = \boldsymbol{N}_0\\ \det \big(\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big) = 1}} (cz+d)^{-k}\bigg(\dfrac{az+b}{cz+d}\bigg)^{-s}, \\T_{\boldsymbol{M}_0,\geq\boldsymbol{N}_0,s}(z) &:= \, e^{i{\pi}s/{2}} \displaystyle\sum_{a^2+b^2 = \boldsymbol{M}_0} \displaystyle\sum_{N \in \mathbb{Z} \atop N\geq \boldsymbol{N}_0} \displaystyle\sum_{\substack{c^2+d^2 = N\\ \det \big(\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big) = 1}}(cz+d)^{-k}\bigg(\dfrac{az+b}{cz+d}\bigg)^{-s},\\ T_{\geq \boldsymbol{M}_0,\boldsymbol{N}_0,s}(z) &:= \, e^{i{\pi}s/{2}} \displaystyle\sum_{M \in \mathbb{Z} \atop M \geq \boldsymbol{M}_0} \displaystyle\sum_{a^2+b^2 = M} \displaystyle\sum_{\substack{c^2+d^2 = \boldsymbol{N}_0\\ \det \big(\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big) = 1}}(cz+d)^{-k}\bigg(\dfrac{az+b}{cz+d}\bigg)^{-s}, \\T_{\geq \boldsymbol{M}_0,\geq \boldsymbol{N}_0,s}(z) &:= \, e^{i{\pi}s/{2}} \displaystyle\sum_{M \in \mathbb{Z} \atop M \geq \boldsymbol{M}_0} \displaystyle\sum_{a^2+b^2 = M} \displaystyle\sum_{N \in \mathbb{Z} \atop N \geq \boldsymbol{N}_0} \displaystyle\sum_{\substack{c^2+d^2 = N\\ \det \big(\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big) = 1}}(cz+d)^{-k}\bigg(\dfrac{az+b}{cz+d}\bigg)^{-s}, \end{align*} $$
where
![]() $T_{-,-,s}(z)$
denotes the unique complex-valued holomorphic function associated to the respective series on the right-hand side for
$T_{-,-,s}(z)$
denotes the unique complex-valued holomorphic function associated to the respective series on the right-hand side for
![]() $1<\sigma <k-1$
. Further, let
$1<\sigma <k-1$
. Further, let
![]() $s=\sigma +i\beta $
be a complex point inside the critical strip. Also, let
$s=\sigma +i\beta $
be a complex point inside the critical strip. Also, let
![]() $t>0.$
Then
$t>0.$
Then
Now,
![]() $T_{1,1,s}(it)$
is formed by the matrices in
$T_{1,1,s}(it)$
is formed by the matrices in
![]() $ \{\pm (\begin {smallmatrix} 1 & 0\\ 0 & 1 \end {smallmatrix}), \pm (\begin {smallmatrix} 0 & -1\\ 1 & 0 \end {smallmatrix})\}$
. We therefore get
$ \{\pm (\begin {smallmatrix} 1 & 0\\ 0 & 1 \end {smallmatrix}), \pm (\begin {smallmatrix} 0 & -1\\ 1 & 0 \end {smallmatrix})\}$
. We therefore get
 $$ \begin{align*} T_{1,1,s}(it) = 2 e^{i({\pi}/{2})s}\bigg\{(it)^{-s}+(it)^{-k}\bigg(\frac{-1}{it}\bigg)^{-s}\bigg\} =\frac{2}{t^{s}} + \frac{2(-1)^{k/2}}{t^{k-s}}. \end{align*} $$
$$ \begin{align*} T_{1,1,s}(it) = 2 e^{i({\pi}/{2})s}\bigg\{(it)^{-s}+(it)^{-k}\bigg(\frac{-1}{it}\bigg)^{-s}\bigg\} =\frac{2}{t^{s}} + \frac{2(-1)^{k/2}}{t^{k-s}}. \end{align*} $$
The last equality is true since
![]() $(it)^{-s}=e^{-{i\pi }s/{2}}t^{-s}$
and
$(it)^{-s}=e^{-{i\pi }s/{2}}t^{-s}$
and
![]() $({-1}/{it})^{-s}=e^{-i{\pi }s/{2}}t^{s}$
using Lemma 4.1. The term
$({-1}/{it})^{-s}=e^{-i{\pi }s/{2}}t^{s}$
using Lemma 4.1. The term
![]() $T_{1,\geq 2,s}(it)$
is formed by the matrices of the form
$T_{1,\geq 2,s}(it)$
is formed by the matrices of the form
Thus,
 $$ \begin{align*} T_{1,\geq 2,s}(it) &= 2e^{i{\pi}s/{2}} \sum_{|c| \geq 1} \bigg\{(c+it)^{-k}\bigg(\frac{-1}{c+it}\bigg)^{-s}+(cit+1)^{-k}\bigg(\frac{it}{cit+1}\bigg)^{-s}\bigg\}. \end{align*} $$
$$ \begin{align*} T_{1,\geq 2,s}(it) &= 2e^{i{\pi}s/{2}} \sum_{|c| \geq 1} \bigg\{(c+it)^{-k}\bigg(\frac{-1}{c+it}\bigg)^{-s}+(cit+1)^{-k}\bigg(\frac{it}{cit+1}\bigg)^{-s}\bigg\}. \end{align*} $$
Let
 $$ \begin{align*} T_{1,\geq 2,s}^{\mathrm{main}}(it)&:= 2e^{i{\pi}s/{2}} \sum_{|c| \geq 1} (c+it)^{-k}\bigg(\frac{-1}{c+it}\bigg)^{-s},\\ T_{1,\geq 2,s}^{\mathrm{error}}(it)&:= 2e^{i{\pi}s/{2}} \sum_{|c| \geq 1} (cit+1)^{-k}\bigg(\frac{it}{cit+1}\bigg)^{-s}. \end{align*} $$
$$ \begin{align*} T_{1,\geq 2,s}^{\mathrm{main}}(it)&:= 2e^{i{\pi}s/{2}} \sum_{|c| \geq 1} (c+it)^{-k}\bigg(\frac{-1}{c+it}\bigg)^{-s},\\ T_{1,\geq 2,s}^{\mathrm{error}}(it)&:= 2e^{i{\pi}s/{2}} \sum_{|c| \geq 1} (cit+1)^{-k}\bigg(\frac{it}{cit+1}\bigg)^{-s}. \end{align*} $$
The first term above may be simplified to give
 $$ \begin{align*} T_{1,\geq 2,s}^{\mathrm{main}}(it) &= 2e^{-i{\pi}s/{2}} \sum_{|c| \geq 1} (c+it)^{-(k-s)} \\&= 2(-1)^{k/2}\bigg\{e^{i{\pi}(k-s)/{2}} \sum_{c \in \mathbb{Z}} (c+it)^{-(k-s)} - e^{i{\pi}(k-s)/{2}}(it)^{-(k-s)}\bigg\}\\&=2(-1)^{k/2}\bigg\{\frac{(2\pi)^{k-s}}{\Gamma(k-s)}\sum_{n \geq 1} n^{k-s-1}e^{-2\pi nt} - \frac{1}{t^{k-s}}\bigg\}. \end{align*} $$
$$ \begin{align*} T_{1,\geq 2,s}^{\mathrm{main}}(it) &= 2e^{-i{\pi}s/{2}} \sum_{|c| \geq 1} (c+it)^{-(k-s)} \\&= 2(-1)^{k/2}\bigg\{e^{i{\pi}(k-s)/{2}} \sum_{c \in \mathbb{Z}} (c+it)^{-(k-s)} - e^{i{\pi}(k-s)/{2}}(it)^{-(k-s)}\bigg\}\\&=2(-1)^{k/2}\bigg\{\frac{(2\pi)^{k-s}}{\Gamma(k-s)}\sum_{n \geq 1} n^{k-s-1}e^{-2\pi nt} - \frac{1}{t^{k-s}}\bigg\}. \end{align*} $$
The last equality follows from the Lipschitz summation formula,
 $$ \begin{align*} \displaystyle \sum_{n \in \mathbb{Z}} \frac{1}{(\tau+n)^s} &= e^{-\pi i s/2}\frac{(2\pi)^s}{\Gamma(s)} \displaystyle \sum_{n \geq 1} n^{s-1}e^{2\pi i n\tau} \quad \text{for } \mathrm{Re} (s)>1, \tau \in \mathbb{H}. \end{align*} $$
$$ \begin{align*} \displaystyle \sum_{n \in \mathbb{Z}} \frac{1}{(\tau+n)^s} &= e^{-\pi i s/2}\frac{(2\pi)^s}{\Gamma(s)} \displaystyle \sum_{n \geq 1} n^{s-1}e^{2\pi i n\tau} \quad \text{for } \mathrm{Re} (s)>1, \tau \in \mathbb{H}. \end{align*} $$
The term
![]() $T_{1,\geq 2,s}^{\mathrm {error}}(it)$
is easily seen to be bounded above by
$T_{1,\geq 2,s}^{\mathrm {error}}(it)$
is easily seen to be bounded above by
![]() ${\mathcal O}_{\beta }(t^{-k})$
. Indeed, Lemma 4.1 implies that
${\mathcal O}_{\beta }(t^{-k})$
. Indeed, Lemma 4.1 implies that
 $$ \begin{align*} \bigg|\bigg(\frac{it}{cit+1}\bigg)^{-s}\bigg|=\bigg|\bigg(c+\frac{1}{it}\bigg)^{s}\bigg|= \bigg(c^2+\frac{1}{t^2}\bigg)^{\sigma/2}e^{-\beta\arg(c+{1}/{it})}.\end{align*} $$
$$ \begin{align*} \bigg|\bigg(\frac{it}{cit+1}\bigg)^{-s}\bigg|=\bigg|\bigg(c+\frac{1}{it}\bigg)^{s}\bigg|= \bigg(c^2+\frac{1}{t^2}\bigg)^{\sigma/2}e^{-\beta\arg(c+{1}/{it})}.\end{align*} $$
It follows that
 $$ \begin{align} |T_{1,\geq 2,s}^{\mathrm{error}}(it)| &\leq \frac{2}{t^k}e^{-{\pi}\beta/{2}} \sum_{|c| \geq 1} \bigg|c+\frac{1}{it}\bigg|^{-k}\bigg|\bigg(c+\frac{1}{it}\bigg)^{s}\bigg| \nonumber\\ &\leq \frac{4}{t^k}e^{-{\pi}\beta/{2}}\sum_{c \in \mathbb{N}} \bigg(c^2+\frac{1}{t^2}\bigg)^{{-(k-\sigma)/2}}\exp(-\beta\arg(c-{i}/{t})) \nonumber \\ & \leq e^{{\pi}|\beta|/{2}}\frac{4}{t^{k}}\zeta(k-\sigma), \end{align} $$
$$ \begin{align} |T_{1,\geq 2,s}^{\mathrm{error}}(it)| &\leq \frac{2}{t^k}e^{-{\pi}\beta/{2}} \sum_{|c| \geq 1} \bigg|c+\frac{1}{it}\bigg|^{-k}\bigg|\bigg(c+\frac{1}{it}\bigg)^{s}\bigg| \nonumber\\ &\leq \frac{4}{t^k}e^{-{\pi}\beta/{2}}\sum_{c \in \mathbb{N}} \bigg(c^2+\frac{1}{t^2}\bigg)^{{-(k-\sigma)/2}}\exp(-\beta\arg(c-{i}/{t})) \nonumber \\ & \leq e^{{\pi}|\beta|/{2}}\frac{4}{t^{k}}\zeta(k-\sigma), \end{align} $$
since
![]() $ |({\pi }/{2})+\arg (c-{i}/{t})| < ({\pi }/{2})$
. For later use, we also simplify
$ |({\pi }/{2})+\arg (c-{i}/{t})| < ({\pi }/{2})$
. For later use, we also simplify
![]() $T_{1,\geq 2,s}^{\mathrm {error}}(it)$
as follows:
$T_{1,\geq 2,s}^{\mathrm {error}}(it)$
as follows:
 $$ \begin{align} T_{1,\geq 2,s}^{\mathrm{error}}(it)&=\frac{2}{(it)^k}e^{i{\pi}s/{2}} \sum_{|c|\geq 1} (c-{i}/{t})^{-(k-s)} =\frac{2}{t^k}e^{i{\pi}(k-s)/{2}} \sum_{|c|\geq 1} (c+{i}/{t})^{-(k-s)}\nonumber \\&=\frac{2}{t^k}\frac{(2\pi)^{k-s}}{\Gamma(k-s)}\sum_{n \geq 1} n^{k-s-1}e^{-2\pi n/t} - \frac{2}{t^{s}}. \end{align} $$
$$ \begin{align} T_{1,\geq 2,s}^{\mathrm{error}}(it)&=\frac{2}{(it)^k}e^{i{\pi}s/{2}} \sum_{|c|\geq 1} (c-{i}/{t})^{-(k-s)} =\frac{2}{t^k}e^{i{\pi}(k-s)/{2}} \sum_{|c|\geq 1} (c+{i}/{t})^{-(k-s)}\nonumber \\&=\frac{2}{t^k}\frac{(2\pi)^{k-s}}{\Gamma(k-s)}\sum_{n \geq 1} n^{k-s-1}e^{-2\pi n/t} - \frac{2}{t^{s}}. \end{align} $$
For fixed
![]() $N \in \mathbb {N}$
,
$N \in \mathbb {N}$
,
![]() $T_{N,1}(z)$
is formed precisely from the matrices in
$T_{N,1}(z)$
is formed precisely from the matrices in
 $$ \begin{align*}\left\{\left(\begin{matrix} a & -1 \\ 1 & 0 \end{matrix}\right), \left(\begin{matrix} a & 1 \\ -1 & 0 \end{matrix}\right), \left(\begin{matrix} 1 & a \\ 0 & 1 \end{matrix}\right), \left(\begin{matrix} -1 & a \\ 0 & -1 \end{matrix}\right)~\bigg|~a \in \mathbb{Z}, a^2+1=N \right\}.\end{align*} $$
$$ \begin{align*}\left\{\left(\begin{matrix} a & -1 \\ 1 & 0 \end{matrix}\right), \left(\begin{matrix} a & 1 \\ -1 & 0 \end{matrix}\right), \left(\begin{matrix} 1 & a \\ 0 & 1 \end{matrix}\right), \left(\begin{matrix} -1 & a \\ 0 & -1 \end{matrix}\right)~\bigg|~a \in \mathbb{Z}, a^2+1=N \right\}.\end{align*} $$
Performing similar computations to those above, one can see that
 $$ \begin{align*} T_{\geq 2,1,s}(it) = \sum_{N\geq 2} T_{N,1}(it) = 2e^{i{\pi}s/{2}} \sum_{|a| \geq 1} \bigg\{(it)^{-k}\bigg(a+\frac{i}{t}\bigg)^{-s}+(a+it)^{-s}\bigg\}. \end{align*} $$
$$ \begin{align*} T_{\geq 2,1,s}(it) = \sum_{N\geq 2} T_{N,1}(it) = 2e^{i{\pi}s/{2}} \sum_{|a| \geq 1} \bigg\{(it)^{-k}\bigg(a+\frac{i}{t}\bigg)^{-s}+(a+it)^{-s}\bigg\}. \end{align*} $$
Let
![]() $T_{\geq 2,1,s}^{\mathrm {error}}(it)$
denote the first sum
$T_{\geq 2,1,s}^{\mathrm {error}}(it)$
denote the first sum
![]() $2e^{i{\pi }s/{2}} \sum _{|a| \geq 1} (it)^{-k}(a+{i}/{t})^{-s}$
. From its definition, we obtain the following equality and bound:
$2e^{i{\pi }s/{2}} \sum _{|a| \geq 1} (it)^{-k}(a+{i}/{t})^{-s}$
. From its definition, we obtain the following equality and bound:
 $$ \begin{align} |T_{\geq 2,1,s}^{\mathrm{error}}(it)| = \bigg|\frac{2}{(it)^k}\bigg\{\frac{(2\pi)^s}{\Gamma(s)} \sum_{n\geq 1} n^{s-1}e^{-2\pi n/t}-t^s\bigg\}\bigg| \leq 4e^{{\pi}|\beta|/{2}}\dfrac{\zeta(\sigma)}{t^k}. \end{align} $$
$$ \begin{align} |T_{\geq 2,1,s}^{\mathrm{error}}(it)| = \bigg|\frac{2}{(it)^k}\bigg\{\frac{(2\pi)^s}{\Gamma(s)} \sum_{n\geq 1} n^{s-1}e^{-2\pi n/t}-t^s\bigg\}\bigg| \leq 4e^{{\pi}|\beta|/{2}}\dfrac{\zeta(\sigma)}{t^k}. \end{align} $$
The second sum, denoted by
![]() $T_{\geq 2,1,s}^{\mathrm {main}}(it)$
, may also be simplified using the Lipschitz summation formula as before to obtain
$T_{\geq 2,1,s}^{\mathrm {main}}(it)$
, may also be simplified using the Lipschitz summation formula as before to obtain
 $$ \begin{align*} T_{\geq 2,1,s}^{\mathrm{main}}(it) = 2\frac{(2\pi)^{s}}{\Gamma(s)}\sum_{n \geq 1} n^{s-1}e^{-2\pi nt} - \frac{2}{t^{s}}. \end{align*} $$
$$ \begin{align*} T_{\geq 2,1,s}^{\mathrm{main}}(it) = 2\frac{(2\pi)^{s}}{\Gamma(s)}\sum_{n \geq 1} n^{s-1}e^{-2\pi nt} - \frac{2}{t^{s}}. \end{align*} $$
The main term (of
![]() $f_{k,s}(it)$
) is
$f_{k,s}(it)$
) is
The remaining terms in the summation (5.2) are brought into the error term (5.7). We therefore have
 $$ \begin{align} T_{\mathrm{main},s}(it)= 2\frac{(2\pi)^{s}}{\Gamma(s)}\sum_{n \geq 1} n^{s-1}e^{-2\pi nt} + 2(-1)^{k/2}\frac{(2\pi)^{k-s}}{\Gamma(k-s)}\sum_{n \geq 1} n^{k-s-1}e^{-2\pi nt}. \end{align} $$
$$ \begin{align} T_{\mathrm{main},s}(it)= 2\frac{(2\pi)^{s}}{\Gamma(s)}\sum_{n \geq 1} n^{s-1}e^{-2\pi nt} + 2(-1)^{k/2}\frac{(2\pi)^{k-s}}{\Gamma(k-s)}\sum_{n \geq 1} n^{k-s-1}e^{-2\pi nt}. \end{align} $$
We remark here that the term on the right-hand side is the contribution of the terms with
![]() $ac=0$
in (5.1) as observed by Kohnen [Reference Khuri-Makdisi, Kohnen and Raji6, page 186]. Also, we note here that the term above vanishes if
$ac=0$
in (5.1) as observed by Kohnen [Reference Khuri-Makdisi, Kohnen and Raji6, page 186]. Also, we note here that the term above vanishes if
![]() $s={k}/{2}$
and
$s={k}/{2}$
and
![]() $k \equiv 2 \bmod 4$
.
$k \equiv 2 \bmod 4$
.
Next we bound the error term. Note that
The final term in (5.2) and (5.7) is bounded above by
 $$ \begin{align} |T_{\geq 2,\geq 2,s}(it)| &\leq~ e^{-{\pi}\beta/{2}}\displaystyle\sum_{M \geq 2} \displaystyle\sum_{a^2+b^2 = M} \displaystyle\sum_{N\geq 2} \sum_{\substack{c^2+d^2= N \\ \det \big(\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big) = 1}} |cit+d|^{-k}\bigg|\bigg(\frac{ait+b}{cit+d}\bigg)^{-s}\bigg| \nonumber \\ &\leq~ \displaystyle\sum_{M \geq 2} \displaystyle\sum_{a^2+b^2 = M} \displaystyle\sum_{N\geq 2} \sum_{\substack{c^2+d^2= N\\ ad-bc=1}} |cit+d|^{-k+\sigma}|ait+b|^{-\sigma} e^{\beta (\arg(({ait+b})/({cit+d}))-({\pi}/{2}))} \nonumber \\ &\leq e^{{\pi}|\beta|/{2}}\displaystyle\sum_{\substack{a^2+b^2 \geq 2 \\ (a,b)=1}} \frac{1}{|ait+b|^{\sigma}} \displaystyle\sum_{\substack{c^2+d^2 \geq 2\\ (c,d)=1}} \frac{1}{|cit+d|^{k-\sigma}}. \end{align} $$
$$ \begin{align} |T_{\geq 2,\geq 2,s}(it)| &\leq~ e^{-{\pi}\beta/{2}}\displaystyle\sum_{M \geq 2} \displaystyle\sum_{a^2+b^2 = M} \displaystyle\sum_{N\geq 2} \sum_{\substack{c^2+d^2= N \\ \det \big(\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big) = 1}} |cit+d|^{-k}\bigg|\bigg(\frac{ait+b}{cit+d}\bigg)^{-s}\bigg| \nonumber \\ &\leq~ \displaystyle\sum_{M \geq 2} \displaystyle\sum_{a^2+b^2 = M} \displaystyle\sum_{N\geq 2} \sum_{\substack{c^2+d^2= N\\ ad-bc=1}} |cit+d|^{-k+\sigma}|ait+b|^{-\sigma} e^{\beta (\arg(({ait+b})/({cit+d}))-({\pi}/{2}))} \nonumber \\ &\leq e^{{\pi}|\beta|/{2}}\displaystyle\sum_{\substack{a^2+b^2 \geq 2 \\ (a,b)=1}} \frac{1}{|ait+b|^{\sigma}} \displaystyle\sum_{\substack{c^2+d^2 \geq 2\\ (c,d)=1}} \frac{1}{|cit+d|^{k-\sigma}}. \end{align} $$
Here
![]() $ |ait+b|^{\sigma } = |-ait+b|^{\sigma }$
for any
$ |ait+b|^{\sigma } = |-ait+b|^{\sigma }$
for any
![]() $a\in \mathbb {N}$
and
$a\in \mathbb {N}$
and
![]() $b\in \mathbb {Z}$
. It follows that
$b\in \mathbb {Z}$
. It follows that
 $$ \begin{align*} \displaystyle\sum_{\substack{a^2+b^2 \geq 2 \\ (a,b)=1}} \frac{1}{|ait+b|^{\sigma}} &= 2\displaystyle\sum_{a=1}^{\infty} \frac{1}{a^{\sigma}} \displaystyle\sum_{b \in \mathbb{Z}\setminus\{0\} \atop (b,a)=1} \frac{1}{|it+{b}/{a}|^{\sigma}} \; = 2\displaystyle\sum_{a=1}^{\infty} \frac{1}{a^{\sigma}} \displaystyle\sum_{\substack{0 < r <a \\ (r,a)=1}} \displaystyle\sum_{q \in \mathbb{Z}} \frac{1}{|it+q+{r}/{a}|^{\sigma}}. \end{align*} $$
$$ \begin{align*} \displaystyle\sum_{\substack{a^2+b^2 \geq 2 \\ (a,b)=1}} \frac{1}{|ait+b|^{\sigma}} &= 2\displaystyle\sum_{a=1}^{\infty} \frac{1}{a^{\sigma}} \displaystyle\sum_{b \in \mathbb{Z}\setminus\{0\} \atop (b,a)=1} \frac{1}{|it+{b}/{a}|^{\sigma}} \; = 2\displaystyle\sum_{a=1}^{\infty} \frac{1}{a^{\sigma}} \displaystyle\sum_{\substack{0 < r <a \\ (r,a)=1}} \displaystyle\sum_{q \in \mathbb{Z}} \frac{1}{|it+q+{r}/{a}|^{\sigma}}. \end{align*} $$
By Lemma 4.5, the inner sum on the right-hand side is
![]() ${\mathcal O}({1}/{t^{\sigma -1}})$
if
${\mathcal O}({1}/{t^{\sigma -1}})$
if
![]() $t\geq 1$
. Note that up to this point, we have only assumed that
$t\geq 1$
. Note that up to this point, we have only assumed that
![]() $t>0$
. This follows since
$t>0$
. This follows since
![]() $\phi (a) < a$
and
$\phi (a) < a$
and
![]() $\sum _{a=1}^{\infty } {1}/{a^{\sigma -1}}$
converges. More precisely,
$\sum _{a=1}^{\infty } {1}/{a^{\sigma -1}}$
converges. More precisely,
 $$ \begin{align*}\displaystyle\sum_{\substack{a^2+b^2 \geq 2 \\ (a,b)=1}} \frac{1}{|ait+b|^{\sigma}} < 14 \frac{\zeta(\sigma-1)}{t^{\sigma-1}} \quad\mbox{and}\quad \displaystyle\sum_{\substack{c^2+d^2 \geq 2 \\ (c,d)=1}} \frac{1}{|cit+d|^{k-\sigma}} < 14 \frac{\zeta(k-\sigma-1)}{t^{k-\sigma-1}}. \end{align*} $$
$$ \begin{align*}\displaystyle\sum_{\substack{a^2+b^2 \geq 2 \\ (a,b)=1}} \frac{1}{|ait+b|^{\sigma}} < 14 \frac{\zeta(\sigma-1)}{t^{\sigma-1}} \quad\mbox{and}\quad \displaystyle\sum_{\substack{c^2+d^2 \geq 2 \\ (c,d)=1}} \frac{1}{|cit+d|^{k-\sigma}} < 14 \frac{\zeta(k-\sigma-1)}{t^{k-\sigma-1}}. \end{align*} $$
Hence, by (5.8),
 $$ \begin{align*} |T_{\geq 2,\geq 2,s}(it)| < e^{{\pi}|\beta|/{2}} \frac{14^2\times \zeta^2(4.5)}{t^{k-2}} < e^{{\pi}|\beta|/{2}} \frac{250}{t^{k-2}}. \end{align*} $$
$$ \begin{align*} |T_{\geq 2,\geq 2,s}(it)| < e^{{\pi}|\beta|/{2}} \frac{14^2\times \zeta^2(4.5)}{t^{k-2}} < e^{{\pi}|\beta|/{2}} \frac{250}{t^{k-2}}. \end{align*} $$
(Note that the condition
![]() $k \geq 12$
implies that
$k \geq 12$
implies that
![]() $\sigma $
and
$\sigma $
and
![]() $k-\sigma $
are greater than or equal to
$k-\sigma $
are greater than or equal to
![]() $5.5$
.) Now, (5.3) and (5.5), together with the above fact, imply that as long as
$5.5$
.) Now, (5.3) and (5.5), together with the above fact, imply that as long as
![]() $k \geq 12$
and
$k \geq 12$
and
![]() $t\geq 1$
,
$t\geq 1$
,
Thus, for all
![]() $ t \ge 1$
and all even integers
$ t \ge 1$
and all even integers
![]() $k \ge 12$
,
$k \ge 12$
,
 $$ \begin{align*} f_{k,s}(it) = 2\frac{(2\pi)^{s}}{\Gamma(s)}\sum_{n \geq 1} n^{s-1}e^{-2\pi nt} + 2(-1)^{k/2}\frac{(2\pi)^{k-s}}{\Gamma(k-s)} \sum_{n \geq 1} n^{k-s-1}e^{-2\pi nt} + C_{\beta}\bigg(\frac{1}{t^{k-2}}\bigg), \end{align*} $$
$$ \begin{align*} f_{k,s}(it) = 2\frac{(2\pi)^{s}}{\Gamma(s)}\sum_{n \geq 1} n^{s-1}e^{-2\pi nt} + 2(-1)^{k/2}\frac{(2\pi)^{k-s}}{\Gamma(k-s)} \sum_{n \geq 1} n^{k-s-1}e^{-2\pi nt} + C_{\beta}\bigg(\frac{1}{t^{k-2}}\bigg), \end{align*} $$
where
![]() $C_{\beta } \leq 300e^{{\pi }|\beta |/{2}}$
. This completes the proof of Theorem 3.1.
$C_{\beta } \leq 300e^{{\pi }|\beta |/{2}}$
. This completes the proof of Theorem 3.1.
6 Proof of Corollary 3.2
We remark here that from (2.4) and (3.1) it follows that
 $$ \begin{align} f_{k,s_1} = \displaystyle\sum_{f \in \mathcal{B}_k} \langle f_{k,s_1},f\rangle \dfrac{f}{\langle f,f \rangle} = \dfrac{(-1)^{k/2}\pi \Gamma(k-1)}{2^{k-3}\Gamma(s_1)\Gamma(k-s_1)} \displaystyle\sum_{f\in \mathcal{B}_k} L^*(f,s_1) \dfrac{f}{\langle f,f\rangle}. \end{align} $$
$$ \begin{align} f_{k,s_1} = \displaystyle\sum_{f \in \mathcal{B}_k} \langle f_{k,s_1},f\rangle \dfrac{f}{\langle f,f \rangle} = \dfrac{(-1)^{k/2}\pi \Gamma(k-1)}{2^{k-3}\Gamma(s_1)\Gamma(k-s_1)} \displaystyle\sum_{f\in \mathcal{B}_k} L^*(f,s_1) \dfrac{f}{\langle f,f\rangle}. \end{align} $$
To prove Corollary (3.2), we need the following fact.
Lemma 6.1. Let
![]() $k\geq 12, k \not =14$
be an even integer. Then
$k\geq 12, k \not =14$
be an even integer. Then
![]() $f(ki)> 0$
for any
$f(ki)> 0$
for any
![]() $f \in \mathcal {B}_k$
.
$f \in \mathcal {B}_k$
.
Proof. Note that
![]() $f(ki)=e^{-2\pi k}+\sum _{n\geq 2} a_f(n)e^{-2\pi nk}$
. Multiplying by
$f(ki)=e^{-2\pi k}+\sum _{n\geq 2} a_f(n)e^{-2\pi nk}$
. Multiplying by
![]() $e^{2\pi k}$
on both sides,
$e^{2\pi k}$
on both sides,
It is enough to prove that the summation term on the right-hand side is bounded above by
![]() $\tfrac 12$
. Using Hardy’s estimate
$\tfrac 12$
. Using Hardy’s estimate
![]() $ |a_f(n)| \le 3n^{k/2}, $
we have
$ |a_f(n)| \le 3n^{k/2}, $
we have
 $$ \begin{align*} \bigg|\sum_{n\geq 1} a_f(n+1)e^{-2\pi nk}\bigg| &\leq 3 \sum_{n\geq 1} (n+1)^{k/2}e^{-2\pi nk} \leq \frac{3}{e^{\pi k}} \sum_{n\geq 1} \frac{1}{(n+1)^{k/2}} \leq \frac{3}{e^{\pi k}} \zeta(k/2) < \frac{1}{2}, \end{align*} $$
$$ \begin{align*} \bigg|\sum_{n\geq 1} a_f(n+1)e^{-2\pi nk}\bigg| &\leq 3 \sum_{n\geq 1} (n+1)^{k/2}e^{-2\pi nk} \leq \frac{3}{e^{\pi k}} \sum_{n\geq 1} \frac{1}{(n+1)^{k/2}} \leq \frac{3}{e^{\pi k}} \zeta(k/2) < \frac{1}{2}, \end{align*} $$
since
![]() $e^{2\pi nk}> (e^{\pi }(n+1))^k$
for all
$e^{2\pi nk}> (e^{\pi }(n+1))^k$
for all
![]() $n\geq 1$
, which proves the claim.
$n\geq 1$
, which proves the claim.
Proof of Corollary 3.2
For the remainder of this section, we assume
![]() $4 \mid k$
. The functional equation (3.2) allows us to choose
$4 \mid k$
. The functional equation (3.2) allows us to choose
![]() $\sigma \;\in \;[{k}/{2},{(k+1)}/{2}]$
without loss of generality. From (6.1),
$\sigma \;\in \;[{k}/{2},{(k+1)}/{2}]$
without loss of generality. From (6.1),
 $$ \begin{align} f_{k,\sigma}(ik) = \dfrac{\pi \Gamma(k-1)(2\pi)^{-\sigma}}{2^{k-3}\Gamma(k-\sigma)} \displaystyle\sum_{f\in \mathcal{B}_k} \dfrac{L(f,\sigma)}{\langle f,f\rangle}f(ik). \end{align} $$
$$ \begin{align} f_{k,\sigma}(ik) = \dfrac{\pi \Gamma(k-1)(2\pi)^{-\sigma}}{2^{k-3}\Gamma(k-\sigma)} \displaystyle\sum_{f\in \mathcal{B}_k} \dfrac{L(f,\sigma)}{\langle f,f\rangle}f(ik). \end{align} $$
To produce a Hecke eigenform whose L-value is positive at
![]() $\sigma $
, we use Theorem 3.1:
$\sigma $
, we use Theorem 3.1:
 $$ \begin{align*} f_{k,\sigma}(ik) = 2\frac{(2\pi)^{\sigma}}{\Gamma(\sigma)}\sum_{n \geq 1} n^{\sigma-1}e^{-2\pi nk} + 2\frac{(2\pi)^{k-\sigma}}{\Gamma(k-\sigma)}\sum_{n \geq 1} n^{k-\sigma-1}e^{-2\pi nk} + T_{\mathrm{error},\sigma}(ik), \end{align*} $$
$$ \begin{align*} f_{k,\sigma}(ik) = 2\frac{(2\pi)^{\sigma}}{\Gamma(\sigma)}\sum_{n \geq 1} n^{\sigma-1}e^{-2\pi nk} + 2\frac{(2\pi)^{k-\sigma}}{\Gamma(k-\sigma)}\sum_{n \geq 1} n^{k-\sigma-1}e^{-2\pi nk} + T_{\mathrm{error},\sigma}(ik), \end{align*} $$
where
![]() $T_{\mathrm {error},\sigma }(ik) \ll {1}/{k^{k-2}}$
for large enough k. From Lemma 4.3(b), the main term is bounded below by
$T_{\mathrm {error},\sigma }(ik) \ll {1}/{k^{k-2}}$
for large enough k. From Lemma 4.3(b), the main term is bounded below by
 $$ \begin{align*} T_{\mathrm{main},\sigma}(ik) &> 2\frac{(2\pi)^{k-\sigma}}{\Gamma(k-\sigma)}e^{-2\pi k} \gg \bigg(\frac{\sqrt{4\pi e}}{e^{2\pi}}\bigg)^k k^{-{(k-1)}/{2}}, \end{align*} $$
$$ \begin{align*} T_{\mathrm{main},\sigma}(ik) &> 2\frac{(2\pi)^{k-\sigma}}{\Gamma(k-\sigma)}e^{-2\pi k} \gg \bigg(\frac{\sqrt{4\pi e}}{e^{2\pi}}\bigg)^k k^{-{(k-1)}/{2}}, \end{align*} $$
as
![]() $k\rightarrow \infty $
. Hence,
$k\rightarrow \infty $
. Hence,
![]() $f_{k,\sigma }(ik)> 0$
for
$f_{k,\sigma }(ik)> 0$
for
![]() $k \gg 1$
,
$k \gg 1$
,
![]() $4 \mid k$
. Combining this with (6.2) and Lemma 6.1, we deduce that there is a Hecke eigenform f in
$4 \mid k$
. Combining this with (6.2) and Lemma 6.1, we deduce that there is a Hecke eigenform f in
![]() $S_k$
such that
$S_k$
such that
![]() $L(f,\sigma )>0$
. Now, Corollary 3.2 easily follows using the same method as in [Reference Manickam, Murty and Sandeep9, Corollary 2.2.1].
$L(f,\sigma )>0$
. Now, Corollary 3.2 easily follows using the same method as in [Reference Manickam, Murty and Sandeep9, Corollary 2.2.1].
7 Proof of Theorem 3.3
Let
![]() $T,\delta ,\delta ^{\prime }$
be fixed constants as in the statement of Theorem 3.3. Let
$T,\delta ,\delta ^{\prime }$
be fixed constants as in the statement of Theorem 3.3. Let
![]() $(s_1,s_2) \in R_{T,\delta ,\delta ^{\prime }}$
, where
$(s_1,s_2) \in R_{T,\delta ,\delta ^{\prime }}$
, where
![]() $s_j=\sigma _j+i\beta _j$
with
$s_j=\sigma _j+i\beta _j$
with
![]() $\sigma _j=k/2+\epsilon _j$
for
$\sigma _j=k/2+\epsilon _j$
for
![]() $j=1,2$
. Recall (from (3.2)) that
$j=1,2$
. Recall (from (3.2)) that
![]() $f_{k,s_1}$
satisfies the functional equation
$f_{k,s_1}$
satisfies the functional equation
![]() $f_{k,s_1} = (-1)^{k/2}f_{k,k-s_1}$
. Combining this with the functional equation of the L-function (2.1) gives
$f_{k,s_1} = (-1)^{k/2}f_{k,k-s_1}$
. Combining this with the functional equation of the L-function (2.1) gives
We can therefore assume
![]() $s_1$
and
$s_1$
and
![]() $s_2$
are on the right half of the critical strip, that is, from (1.2),
$s_2$
are on the right half of the critical strip, that is, from (1.2),
![]() $ {(k+1)}/{2} \geq \sigma _2 \geq \sigma _1+\delta ^{\prime }> \sigma _1 > {k}/{2}. $
From (5.2) and (5.6),
$ {(k+1)}/{2} \geq \sigma _2 \geq \sigma _1+\delta ^{\prime }> \sigma _1 > {k}/{2}. $
From (5.2) and (5.6),
 $$ \begin{align} L^*(f_{k,s_1},s_2) &= \int_{0}^{\infty} f_{k,s_1}(it)t^{s_2-1}\,dt\nonumber\\ & = \int_{0}^{\infty} \!\!\bigg(\frac{2(-1)^{k/2}(2\pi)^{k-s_1}}{\Gamma(k-s_1)}\sum_{n \geq 1} n^{k-s_1-1}e^{-2\pi nt}\nonumber \\ &\qquad \quad + \frac{2(2\pi)^{s_1}}{\Gamma(s_1)}\sum_{n \geq 1} n^{s_1-1}e^{-2\pi nt} + T_{\mathrm{error},s_1}(it)\bigg)t^{s_2-1} \,dt\nonumber \\ &=2(-1)^{k/2}\frac{(2\pi)^{k-s_1}}{\Gamma(k-s_1)}\sum_{n \geq 1} n^{k-s_1-1}\int_{0}^{\infty} e^{-2\pi nt}t^{s_2-1}\,dt \nonumber\\&\quad + 2\frac{(2\pi)^{s_1}}{\Gamma(s_1)}\sum_{n \geq 1} n^{s_1-1}\int_{0}^{\infty} e^{-2\pi nt}t^{s_2-1}\,dt + L^*(T_{\mathrm{error},s_1},s_2)\nonumber\\ &=2\frac{(2\pi)^{s_1-s_2}}{\Gamma(s_1)}\Gamma(s_2)\zeta(s_2-s_1+1)\nonumber\\&\quad +2(-1)^{k/2}\frac{(2\pi)^{k-s_1-s_2}}{\Gamma(k-s_1)}\Gamma(s_2)\zeta(s_2-(k-s_1)+1) +L^*(T_{\mathrm{error},s_1},s_2). \end{align} $$
$$ \begin{align} L^*(f_{k,s_1},s_2) &= \int_{0}^{\infty} f_{k,s_1}(it)t^{s_2-1}\,dt\nonumber\\ & = \int_{0}^{\infty} \!\!\bigg(\frac{2(-1)^{k/2}(2\pi)^{k-s_1}}{\Gamma(k-s_1)}\sum_{n \geq 1} n^{k-s_1-1}e^{-2\pi nt}\nonumber \\ &\qquad \quad + \frac{2(2\pi)^{s_1}}{\Gamma(s_1)}\sum_{n \geq 1} n^{s_1-1}e^{-2\pi nt} + T_{\mathrm{error},s_1}(it)\bigg)t^{s_2-1} \,dt\nonumber \\ &=2(-1)^{k/2}\frac{(2\pi)^{k-s_1}}{\Gamma(k-s_1)}\sum_{n \geq 1} n^{k-s_1-1}\int_{0}^{\infty} e^{-2\pi nt}t^{s_2-1}\,dt \nonumber\\&\quad + 2\frac{(2\pi)^{s_1}}{\Gamma(s_1)}\sum_{n \geq 1} n^{s_1-1}\int_{0}^{\infty} e^{-2\pi nt}t^{s_2-1}\,dt + L^*(T_{\mathrm{error},s_1},s_2)\nonumber\\ &=2\frac{(2\pi)^{s_1-s_2}}{\Gamma(s_1)}\Gamma(s_2)\zeta(s_2-s_1+1)\nonumber\\&\quad +2(-1)^{k/2}\frac{(2\pi)^{k-s_1-s_2}}{\Gamma(k-s_1)}\Gamma(s_2)\zeta(s_2-(k-s_1)+1) +L^*(T_{\mathrm{error},s_1},s_2). \end{align} $$
Interchanging the summation and integration in the second last step is justified by the Fubini–Tonelli theorem, noting that
![]() $\sum _{n \geq 1} \int _{0}^{\infty } |n^{s_1-1} e^{-2\pi nt}t^{s_2-1}|\,dt <\infty $
since
$\sum _{n \geq 1} \int _{0}^{\infty } |n^{s_1-1} e^{-2\pi nt}t^{s_2-1}|\,dt <\infty $
since
![]() $\mathrm {Re}(s_2)>\mathrm {Re}(s_1)$
and
$\mathrm {Re}(s_2)>\mathrm {Re}(s_1)$
and
![]() $\sum _{n \geq 1} \int _{0}^{\infty } |n^{k-s_1-1} e^{-2\pi nt}t^{s_2-1}|\,dt <\infty $
since
$\sum _{n \geq 1} \int _{0}^{\infty } |n^{k-s_1-1} e^{-2\pi nt}t^{s_2-1}|\,dt <\infty $
since
![]() $\mathrm {Re}(s_2)>\mathrm {Re}(k-s_1)$
. (The notation
$\mathrm {Re}(s_2)>\mathrm {Re}(k-s_1)$
. (The notation
![]() $L^*(T_{\mathrm {error},s_1},s_2)$
makes sense as the Mellin transform of
$L^*(T_{\mathrm {error},s_1},s_2)$
makes sense as the Mellin transform of
![]() $T_{\mathrm {error},s_1}$
. It is well defined as all the other integrals in the equality are finite.) Next, we note that
$T_{\mathrm {error},s_1}$
. It is well defined as all the other integrals in the equality are finite.) Next, we note that
 $$ \begin{align*} L^*(T_{\mathrm{main},s_1},s_2) &:= 2\frac{(2\pi)^{s_1-s_2}}{\Gamma(s_1)}\Gamma(s_2)\zeta(s_2-s_1+1) \\ & \quad +2(-1)^{k/2}\frac{(2\pi)^{k-s_1-s_2}}{\Gamma(k-s_1)}\Gamma(s_2)\zeta(s_2-(k-s_1)+1). \end{align*} $$
$$ \begin{align*} L^*(T_{\mathrm{main},s_1},s_2) &:= 2\frac{(2\pi)^{s_1-s_2}}{\Gamma(s_1)}\Gamma(s_2)\zeta(s_2-s_1+1) \\ & \quad +2(-1)^{k/2}\frac{(2\pi)^{k-s_1-s_2}}{\Gamma(k-s_1)}\Gamma(s_2)\zeta(s_2-(k-s_1)+1). \end{align*} $$
7.1 Estimating the main term
We have
![]() $0 < \epsilon _1 < \epsilon _1 + \delta ^{\prime } \leq \epsilon _2 \leq \tfrac 12$
,
$0 < \epsilon _1 < \epsilon _1 + \delta ^{\prime } \leq \epsilon _2 \leq \tfrac 12$
,
![]() $|\beta _j| \leq T$
and
$|\beta _j| \leq T$
and
![]() $\sum _{j=1}^{2} \epsilon _j \geq \tfrac 12+\delta $
. (Note that this forces
$\sum _{j=1}^{2} \epsilon _j \geq \tfrac 12+\delta $
. (Note that this forces
![]() $\epsilon _1\geq \delta $
.) From (4.1),
$\epsilon _1\geq \delta $
.) From (4.1),
 $$ \begin{align*} \bigg|\frac{\Gamma(s_2)}{\Gamma(k-s_1)}\bigg| \geq \frac{1}{\sqrt{\cosh \pi\beta_2}}\frac{\Gamma(\frac{k}{2}+\epsilon_2)}{\Gamma(\frac{k}{2}-\epsilon_1)} \geq e^{-{\pi|\beta_2|}/{2}}\bigg(\frac{k}{2}+\epsilon_2-1\bigg)^{\epsilon_1+\epsilon_2} \geq \frac{k^{\epsilon_1+\epsilon_2}}{3}e^{-{\pi T}/{2}}. \end{align*} $$
$$ \begin{align*} \bigg|\frac{\Gamma(s_2)}{\Gamma(k-s_1)}\bigg| \geq \frac{1}{\sqrt{\cosh \pi\beta_2}}\frac{\Gamma(\frac{k}{2}+\epsilon_2)}{\Gamma(\frac{k}{2}-\epsilon_1)} \geq e^{-{\pi|\beta_2|}/{2}}\bigg(\frac{k}{2}+\epsilon_2-1\bigg)^{\epsilon_1+\epsilon_2} \geq \frac{k^{\epsilon_1+\epsilon_2}}{3}e^{-{\pi T}/{2}}. \end{align*} $$
Similarly, one can see that
Next, we find a lower bound for
![]() $\zeta (s_1+s_2-k+1)$
. By Lemma (4.6),
$\zeta (s_1+s_2-k+1)$
. By Lemma (4.6),
 $$ \begin{align*} |\zeta(s_1+s_2-k+1)| \geq \frac{\zeta(2(1+\epsilon_2+\epsilon_1))}{\zeta(1+\epsilon_2+\epsilon_1)}> \frac{\zeta(4)}{\zeta(1.5)} = c_1. \end{align*} $$
$$ \begin{align*} |\zeta(s_1+s_2-k+1)| \geq \frac{\zeta(2(1+\epsilon_2+\epsilon_1))}{\zeta(1+\epsilon_2+\epsilon_1)}> \frac{\zeta(4)}{\zeta(1.5)} = c_1. \end{align*} $$
Now, the function
![]() $(x-1)\zeta (x)$
is bounded in the interval
$(x-1)\zeta (x)$
is bounded in the interval
![]() $1 \leq x \leq 2$
. So, set
$1 \leq x \leq 2$
. So, set
Then
![]() $|\zeta (s_2-s_1+1)| \leq \zeta (\epsilon _2-\epsilon _1+1) \leq \zeta (\delta ^{\prime }+1) \leq {c_2}/{\delta ^{\prime }}$
, since
$|\zeta (s_2-s_1+1)| \leq \zeta (\epsilon _2-\epsilon _1+1) \leq \zeta (\delta ^{\prime }+1) \leq {c_2}/{\delta ^{\prime }}$
, since
![]() $\epsilon _2-\epsilon _1 \geq \delta ^{\prime }$
. One therefore sees that
$\epsilon _2-\epsilon _1 \geq \delta ^{\prime }$
. One therefore sees that
 $$ \begin{align} &|L^*(T_{\mathrm{main},s_1},s_2)| \nonumber\\ &\quad \geq 2\bigg\{(2\pi)^{-(\epsilon_1+\epsilon_2)} \bigg|\frac{\Gamma(s_2)}{\Gamma(k-s_1)}\zeta(s_1+s_2-k+1)\bigg| -(2\pi)^{\epsilon_1-\epsilon_2}\bigg|\frac{\Gamma(s_2)}{\Gamma(s_1)}\zeta(\epsilon_2-\epsilon_1+1)\bigg|\bigg\}\nonumber\\ &\quad \geq \frac{c_1}{3\pi}k^{\epsilon_1+\epsilon_2} e^{-{\pi T}/{2}} - \frac{2c_2}{\delta^{\prime}}e^{{\pi T}/{2}} k^{\epsilon_2-\epsilon_1}. \end{align} $$
$$ \begin{align} &|L^*(T_{\mathrm{main},s_1},s_2)| \nonumber\\ &\quad \geq 2\bigg\{(2\pi)^{-(\epsilon_1+\epsilon_2)} \bigg|\frac{\Gamma(s_2)}{\Gamma(k-s_1)}\zeta(s_1+s_2-k+1)\bigg| -(2\pi)^{\epsilon_1-\epsilon_2}\bigg|\frac{\Gamma(s_2)}{\Gamma(s_1)}\zeta(\epsilon_2-\epsilon_1+1)\bigg|\bigg\}\nonumber\\ &\quad \geq \frac{c_1}{3\pi}k^{\epsilon_1+\epsilon_2} e^{-{\pi T}/{2}} - \frac{2c_2}{\delta^{\prime}}e^{{\pi T}/{2}} k^{\epsilon_2-\epsilon_1}. \end{align} $$
7.2 Estimating the error term
Next, we consider the term
![]() $T_{\mathrm {error},s_1}(it)$
. We claim that the component
$T_{\mathrm {error},s_1}(it)$
. We claim that the component
![]() $T_{\geq 2,\geq 2,s_1}(it)$
is modular under the action of
$T_{\geq 2,\geq 2,s_1}(it)$
is modular under the action of
![]() $S:=(\begin {smallmatrix} 0&-1\\ 1&0 \end {smallmatrix})$
, that is, for all
$S:=(\begin {smallmatrix} 0&-1\\ 1&0 \end {smallmatrix})$
, that is, for all
![]() $t>0$
,
$t>0$
,
This follows since
 $$ \begin{align} T_{\geq2,\geq2,s_1}(it) &= e^{i{\pi}s_1/2} \displaystyle\sum_{a^2+b^2 \geq 2} \sum_{\substack{c^2+d^2 \geq 2\\ \det \big(\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big) = 1}} (cit+d)^{-k}\bigg(\frac{ait+b}{cit+d}\bigg)^{-s_1}\nonumber\\ &=e^{i{\pi}s_1/{2}} \displaystyle\sum_{a^2+b^2 \geq 2} \sum_{\substack{c^2+d^2 \geq 2\\ \det \big(\begin{smallmatrix} a & b \\ c & d \end{smallmatrix} \big)= 1}} (it)^{-k}(-d(i/t)+c)^{-k}\bigg(\frac{-b(i/t)+a}{-d(i/t)+c}\bigg)^{-s}\nonumber\\ &=(it)^{-k}T_{\geq 2,\geq 2,s_1}(i/t). \end{align} $$
$$ \begin{align} T_{\geq2,\geq2,s_1}(it) &= e^{i{\pi}s_1/2} \displaystyle\sum_{a^2+b^2 \geq 2} \sum_{\substack{c^2+d^2 \geq 2\\ \det \big(\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\big) = 1}} (cit+d)^{-k}\bigg(\frac{ait+b}{cit+d}\bigg)^{-s_1}\nonumber\\ &=e^{i{\pi}s_1/{2}} \displaystyle\sum_{a^2+b^2 \geq 2} \sum_{\substack{c^2+d^2 \geq 2\\ \det \big(\begin{smallmatrix} a & b \\ c & d \end{smallmatrix} \big)= 1}} (it)^{-k}(-d(i/t)+c)^{-k}\bigg(\frac{-b(i/t)+a}{-d(i/t)+c}\bigg)^{-s}\nonumber\\ &=(it)^{-k}T_{\geq 2,\geq 2,s_1}(i/t). \end{align} $$
Thus,
 $$ \begin{align*}L^*(T_{\geq 2,\geq 2,s_1},s_2) = \int_{1}^{\infty} T_{\geq 2,\geq 2,s_1}(it)(t^{s_2}+(-1)^{k/2}t^{k-s_2})\,\frac{dt}{t} \end{align*} $$
$$ \begin{align*}L^*(T_{\geq 2,\geq 2,s_1},s_2) = \int_{1}^{\infty} T_{\geq 2,\geq 2,s_1}(it)(t^{s_2}+(-1)^{k/2}t^{k-s_2})\,\frac{dt}{t} \end{align*} $$
which implies that
 $$ \begin{align} |L^*(T_{\geq 2,\geq 2,s_1},s_2)| & \leq 250e^{{\pi T}/{2}}\bigg(\int_{1}^{\infty} \frac{1}{t^{k-2}}(t^{\sigma_2}+t^{k-\sigma_2})\,\frac{dt}{t}\bigg)\nonumber\\ & \leq 250e^{{\pi T}/{2}}\bigg( \frac{1}{k-\sigma_2-2} + \frac{1}{\sigma_2-2}\bigg) \leq \frac{2000e^{{\pi T}/{2}}}{k} \end{align} $$
$$ \begin{align} |L^*(T_{\geq 2,\geq 2,s_1},s_2)| & \leq 250e^{{\pi T}/{2}}\bigg(\int_{1}^{\infty} \frac{1}{t^{k-2}}(t^{\sigma_2}+t^{k-\sigma_2})\,\frac{dt}{t}\bigg)\nonumber\\ & \leq 250e^{{\pi T}/{2}}\bigg( \frac{1}{k-\sigma_2-2} + \frac{1}{\sigma_2-2}\bigg) \leq \frac{2000e^{{\pi T}/{2}}}{k} \end{align} $$
for all
![]() $k \geq 12$
. However, the other terms
$k \geq 12$
. However, the other terms
![]() $T_{\geq 2,1,s}^{\mathrm {error}}(it)$
and
$T_{\geq 2,1,s}^{\mathrm {error}}(it)$
and
![]() $T_{1,\geq 2,s}^{\mathrm {error}}(it)$
in
$T_{1,\geq 2,s}^{\mathrm {error}}(it)$
in
![]() $T_{\mathrm {error},s}(it)$
are not invariant under S, so we estimate them individually. Note that
$T_{\mathrm {error},s}(it)$
are not invariant under S, so we estimate them individually. Note that
 $$ \begin{align*} L^*(T_{\mathrm{error},s_1},s_2)=L^*(T_{\geq 2,\geq 2,s_1},s_2)+\bigg(\int_{0}^{1}+\int_{1}^{\infty}\bigg)(T_{\geq 2,1,s_1}^{\mathrm{error}}(it) + T_{1,\geq 2,s_1}^{\mathrm{error}}(it))t^{s_2-1}\,dt. \end{align*} $$
$$ \begin{align*} L^*(T_{\mathrm{error},s_1},s_2)=L^*(T_{\geq 2,\geq 2,s_1},s_2)+\bigg(\int_{0}^{1}+\int_{1}^{\infty}\bigg)(T_{\geq 2,1,s_1}^{\mathrm{error}}(it) + T_{1,\geq 2,s_1}^{\mathrm{error}}(it))t^{s_2-1}\,dt. \end{align*} $$
Here, using the bounds in (5.3) and (5.5), we get
 $$ \begin{align} \bigg|\int_{1}^{\infty} (T_{\geq 2,1,s_1}^{\mathrm{error}}(it) + T_{1,\geq 2,s_1}^{\mathrm{error}}(it))t^{s_2-1} \,dt \bigg| &\leq 10e^{{\pi T}/{2}}\bigg(\int_{1}^{\infty} t^{\sigma_2-1-k} \,dt\bigg)\leq\frac{40e^{{\pi T}/{2}}}{k}, \end{align} $$
$$ \begin{align} \bigg|\int_{1}^{\infty} (T_{\geq 2,1,s_1}^{\mathrm{error}}(it) + T_{1,\geq 2,s_1}^{\mathrm{error}}(it))t^{s_2-1} \,dt \bigg| &\leq 10e^{{\pi T}/{2}}\bigg(\int_{1}^{\infty} t^{\sigma_2-1-k} \,dt\bigg)\leq\frac{40e^{{\pi T}/{2}}}{k}, \end{align} $$
again for all
![]() $k \geq 12$
. However, these estimates are not useful when
$k \geq 12$
. However, these estimates are not useful when
![]() $0<t<1$
. Therefore, we proceed as follows. From (4.1) and (5.4), we see that
$0<t<1$
. Therefore, we proceed as follows. From (4.1) and (5.4), we see that
 $$ \begin{align*}|T_{1,\geq 2,s_1}^{\mathrm{error}}(it)|\leq \frac{2}{t^k} (\cosh{\pi \beta_1})^{{1}/{2}}\frac{(2\pi)^{k-\sigma_1}}{\Gamma(k-\sigma_1)}\sum_{n\geq 1} n^{k-\sigma_1-1} e^{{-2\pi n}/{t}}+\frac{2}{t^{\sigma_1}}.\end{align*} $$
$$ \begin{align*}|T_{1,\geq 2,s_1}^{\mathrm{error}}(it)|\leq \frac{2}{t^k} (\cosh{\pi \beta_1})^{{1}/{2}}\frac{(2\pi)^{k-\sigma_1}}{\Gamma(k-\sigma_1)}\sum_{n\geq 1} n^{k-\sigma_1-1} e^{{-2\pi n}/{t}}+\frac{2}{t^{\sigma_1}}.\end{align*} $$
From Lemma 4.4, it follows that there exist absolute constants
![]() $M_0$
and
$M_0$
and
![]() $K_0$
such that
$K_0$
such that
 $$ \begin{align*} &\sum_{n\geq 1} n^{k-\sigma_1-1} e^{-2\pi nu} \leq M_0 \bigg(\frac{k-\sigma_1}{e}\bigg)^{k-\sigma_1}\frac{1}{(2\pi u)^{k-\sigma_1}}, \end{align*} $$
$$ \begin{align*} &\sum_{n\geq 1} n^{k-\sigma_1-1} e^{-2\pi nu} \leq M_0 \bigg(\frac{k-\sigma_1}{e}\bigg)^{k-\sigma_1}\frac{1}{(2\pi u)^{k-\sigma_1}}, \end{align*} $$
for
![]() $k \geq K_0$
uniformly for
$k \geq K_0$
uniformly for
![]() $u \geq 1$
. (Here we have replaced
$u \geq 1$
. (Here we have replaced
![]() ${1}/{t}$
by u.) Thus,
${1}/{t}$
by u.) Thus,
 $$ \begin{align*} &\bigg|\int_{0}^{1} T_{1,\geq 2,s_1}^{\mathrm{error}}(it) t^{s_2-1}\,dt\bigg|\nonumber \\&\quad\leq 2 (\cosh{\pi \beta_1})^{{1}/{2}}\frac{(2\pi)^{k-\sigma_1}}{\Gamma(k-\sigma_1)}\int_{1}^{\infty} \sum_{n\geq 1} n^{k-\sigma_1-1} e^{-2\pi nu}u^{k-\sigma_2}\,\frac{du}{u}+\frac{2}{\sigma_2-\sigma_1}\nonumber \\ &\quad\ll e^{{\pi T}/{2}}\frac{1}{\Gamma(k-\sigma_1)}\bigg(\frac{k-\sigma_1}{e}\bigg)^{k-\sigma_1}\frac{1}{\sigma_2-\sigma_1}+\frac{2}{\sigma_2-\sigma_1}\\&\quad\ll e^{{\pi T}/{2}}\sqrt{(k-\sigma_1)}~~\frac{1}{\delta^{\prime}} \leq \frac{e^{{\pi T}/{2}}}{\delta^{\prime}}\sqrt{k} \end{align*} $$
$$ \begin{align*} &\bigg|\int_{0}^{1} T_{1,\geq 2,s_1}^{\mathrm{error}}(it) t^{s_2-1}\,dt\bigg|\nonumber \\&\quad\leq 2 (\cosh{\pi \beta_1})^{{1}/{2}}\frac{(2\pi)^{k-\sigma_1}}{\Gamma(k-\sigma_1)}\int_{1}^{\infty} \sum_{n\geq 1} n^{k-\sigma_1-1} e^{-2\pi nu}u^{k-\sigma_2}\,\frac{du}{u}+\frac{2}{\sigma_2-\sigma_1}\nonumber \\ &\quad\ll e^{{\pi T}/{2}}\frac{1}{\Gamma(k-\sigma_1)}\bigg(\frac{k-\sigma_1}{e}\bigg)^{k-\sigma_1}\frac{1}{\sigma_2-\sigma_1}+\frac{2}{\sigma_2-\sigma_1}\\&\quad\ll e^{{\pi T}/{2}}\sqrt{(k-\sigma_1)}~~\frac{1}{\delta^{\prime}} \leq \frac{e^{{\pi T}/{2}}}{\delta^{\prime}}\sqrt{k} \end{align*} $$
where we have used
![]() $\sigma _2-\sigma _1 \geq \delta ^{\prime }$
and the fact that
$\sigma _2-\sigma _1 \geq \delta ^{\prime }$
and the fact that
 $$ \begin{align*}\frac{1}{\Gamma(k-\sigma_1)}\bigg(\frac{k-\sigma_1}{e}\bigg)^{k-\sigma_1} \ll \sqrt{k-\sigma_1}. \end{align*} $$
$$ \begin{align*}\frac{1}{\Gamma(k-\sigma_1)}\bigg(\frac{k-\sigma_1}{e}\bigg)^{k-\sigma_1} \ll \sqrt{k-\sigma_1}. \end{align*} $$
The last inequality follows from Stirling’s estimates in Lemma 4.3(b). Thus,
 $$ \begin{align} \int_{0}^{1} T_{1,\geq 2,s_1}^{\mathrm{error}}(it) t^{s_2-1}\,dt ={\mathcal O}_{T,\delta^{\prime}} (k^{1/2}). \end{align} $$
$$ \begin{align} \int_{0}^{1} T_{1,\geq 2,s_1}^{\mathrm{error}}(it) t^{s_2-1}\,dt ={\mathcal O}_{T,\delta^{\prime}} (k^{1/2}). \end{align} $$
Similarly, it follows that
 $$ \begin{align} \int_{0}^{1} T_{\geq 2,1,s_1}^{\mathrm{error}}(it) t^{s_2-1}dt \ll e^{{\pi T}/{2}}\sqrt{\sigma_1}~~\frac{1}{\sigma_2+\sigma_1-k} = {\mathcal O}_{T}(k^{1/2}). \end{align} $$
$$ \begin{align} \int_{0}^{1} T_{\geq 2,1,s_1}^{\mathrm{error}}(it) t^{s_2-1}dt \ll e^{{\pi T}/{2}}\sqrt{\sigma_1}~~\frac{1}{\sigma_2+\sigma_1-k} = {\mathcal O}_{T}(k^{1/2}). \end{align} $$
The implicit constant in (7.8) has no dependency on
![]() $\delta ^{\prime }$
since we assume
$\delta ^{\prime }$
since we assume
![]() $\sigma _1+\sigma _2-k> \tfrac 12$
. From (5.7), (7.4), (7.6), (7.7) and (7.8), it follows that
$\sigma _1+\sigma _2-k> \tfrac 12$
. From (5.7), (7.4), (7.6), (7.7) and (7.8), it follows that
![]() $ L^*(T_{\mathrm {error},s_1},s_2) = {\mathcal O}_{T,\delta ^{\prime }}(\sqrt {k}). $
Along with the above and (7.2) and (7.3), we have
$ L^*(T_{\mathrm {error},s_1},s_2) = {\mathcal O}_{T,\delta ^{\prime }}(\sqrt {k}). $
Along with the above and (7.2) and (7.3), we have
Thus, it follows that
for sufficiently large
![]() $k \gg _{T, \delta , \delta ^{\prime }} 1$
since
$k \gg _{T, \delta , \delta ^{\prime }} 1$
since
![]() $\epsilon _2+\epsilon _1 \geq \tfrac 12+\delta $
.
$\epsilon _2+\epsilon _1 \geq \tfrac 12+\delta $
.
Given an arbitrary pair of points
![]() $s_1,s_2$
satisfying
$s_1,s_2$
satisfying
![]() $\epsilon _1+\epsilon _2 \geq \tfrac 12+\delta $
on the strict right-hand side of the critical line, that is,
$\epsilon _1+\epsilon _2 \geq \tfrac 12+\delta $
on the strict right-hand side of the critical line, that is,
![]() $\{{k}/{2} < \mathrm {Re}(s_j)\leq {(k+1)}/{2}\}$
, one can always choose the point with smaller real part as the kernel parameter and the other one to be the Mellin transform parameter (unless both points lie on the same vertical line, in which case, clearly, our result does not hold). And, even in situations where either (or both)
$\{{k}/{2} < \mathrm {Re}(s_j)\leq {(k+1)}/{2}\}$
, one can always choose the point with smaller real part as the kernel parameter and the other one to be the Mellin transform parameter (unless both points lie on the same vertical line, in which case, clearly, our result does not hold). And, even in situations where either (or both)
![]() $s_1,~s_2$
assume values strictly to the left of the critical line, by virtue of (7.1), one can perform the appropriate reflection
$s_1,~s_2$
assume values strictly to the left of the critical line, by virtue of (7.1), one can perform the appropriate reflection
![]() $s_j \mapsto k-s_j$
, thus effectively reducing it to a question about a pair of points on the right half of the critical strip. This proves the theorem.
$s_j \mapsto k-s_j$
, thus effectively reducing it to a question about a pair of points on the right half of the critical strip. This proves the theorem.
From (6.1),
 $$ \begin{align} L^*(f_{k,s_1},s_2) &= \int_{1}^{\infty} f_{k,s_1}(it)(t^{s_2}+(-1)^{k/2}t^{k-s_2})\,\frac{dt}{t} \nonumber\\&= \frac{(-1)^{{k}/{2}}\pi \Gamma(k-1)}{2^{k-3}\Gamma(s_1)\Gamma(k-s_1)} \displaystyle\sum_{f \in \mathcal{B}_k} \dfrac{L^*(f,s_1)}{\langle f,f\rangle} L^*(f,s_2). \end{align} $$
$$ \begin{align} L^*(f_{k,s_1},s_2) &= \int_{1}^{\infty} f_{k,s_1}(it)(t^{s_2}+(-1)^{k/2}t^{k-s_2})\,\frac{dt}{t} \nonumber\\&= \frac{(-1)^{{k}/{2}}\pi \Gamma(k-1)}{2^{k-3}\Gamma(s_1)\Gamma(k-s_1)} \displaystyle\sum_{f \in \mathcal{B}_k} \dfrac{L^*(f,s_1)}{\langle f,f\rangle} L^*(f,s_2). \end{align} $$
From (7.9) and (7.10) we immediately observe that, given a pair of points
![]() $s_1,s_2$
in the critical strip such that
$s_1,s_2$
in the critical strip such that
![]() $\epsilon _j$
satisfies the conditions in (1.2), there is at least one eigenform
$\epsilon _j$
satisfies the conditions in (1.2), there is at least one eigenform
![]() $f \in \mathcal {B}_k$
whose L-function is simultaneously nonvanishing at both
$f \in \mathcal {B}_k$
whose L-function is simultaneously nonvanishing at both
![]() $s_1$
and
$s_1$
and
![]() $s_2$
for
$s_2$
for
![]() $k \gg _{T, \delta , \delta ^{\prime }} 1$
. However, one may observe that
$k \gg _{T, \delta , \delta ^{\prime }} 1$
. However, one may observe that
 $$ \begin{align*}\sum_{f \in \mathcal{B}_k} \dfrac{L^*(f,s_1)}{\langle f,f\rangle} L^*(f,s_2) \end{align*} $$
$$ \begin{align*}\sum_{f \in \mathcal{B}_k} \dfrac{L^*(f,s_1)}{\langle f,f\rangle} L^*(f,s_2) \end{align*} $$
is the first Fourier coefficient of
![]() $E_{s_1,k-s_1}^*(z,s_2)$
(as a function of
$E_{s_1,k-s_1}^*(z,s_2)$
(as a function of
![]() $z \in \mathbb {H}$
), and this sum is already known to be nonzero for sufficiently large k (see [Reference Choie, Kohnen and Zhang2, formula (3.1)]). This already guarantees the existence of such a Hecke eigenform as above. However, we improve, albeit partially, the result in [Reference Choie, Kohnen and Zhang2] by explicitly determining a lower bound for the number
$z \in \mathbb {H}$
), and this sum is already known to be nonzero for sufficiently large k (see [Reference Choie, Kohnen and Zhang2, formula (3.1)]). This already guarantees the existence of such a Hecke eigenform as above. However, we improve, albeit partially, the result in [Reference Choie, Kohnen and Zhang2] by explicitly determining a lower bound for the number
![]() $N_k(s_1,s_2)$
in Corollary 3.4.
$N_k(s_1,s_2)$
in Corollary 3.4.
8 Proof of Corollary 3.4
Let
![]() $(s_1,s_2) \in R_{T,\delta ,\delta ^{\prime }}$
. Without loss of generality, as earlier, we assume
$(s_1,s_2) \in R_{T,\delta ,\delta ^{\prime }}$
. Without loss of generality, as earlier, we assume
![]() $s_1$
and
$s_1$
and
![]() $s_2$
on the right half of the critical strip. From (7.10),
$s_2$
on the right half of the critical strip. From (7.10),
 $$ \begin{align} k^{\epsilon_2+\epsilon_1} \ll_{T,\delta^{\prime}} \frac{1}{k 2^{k-3}}\frac{\Gamma(k)}{|\Gamma(s_1)\Gamma(k-s_1)|}\sum_{f\in \mathcal{B}_k} \bigg|\dfrac{L^*(f,s_1)L^*(f,s_2)}{\langle f,f \rangle}\bigg|, \end{align} $$
$$ \begin{align} k^{\epsilon_2+\epsilon_1} \ll_{T,\delta^{\prime}} \frac{1}{k 2^{k-3}}\frac{\Gamma(k)}{|\Gamma(s_1)\Gamma(k-s_1)|}\sum_{f\in \mathcal{B}_k} \bigg|\dfrac{L^*(f,s_1)L^*(f,s_2)}{\langle f,f \rangle}\bigg|, \end{align} $$
for large enough k (as mentioned in (7.9)). By the Phragmén–Lindelöf theorem [Reference Rademacher12],
It is well known that for any normalised Hecke eigenform
![]() $f\in S_k$
,
$f\in S_k$
,
holds for arbitrarily small
![]() $\delta ^{\prime \prime \prime }>0$
[Reference Luo8, page 4]. Thus
$\delta ^{\prime \prime \prime }>0$
[Reference Luo8, page 4]. Thus
where the first relation is from [Reference Cohen and Strömberg3, Corollary 11.12.7(b)]. Using this estimate and (8.2),
 $$ \begin{align*} \sum_{f\in \mathcal{B}_k} \bigg\lvert\dfrac{L^*(f,s_1)L^*(f,s_2)}{\langle f,f \rangle}\bigg\rvert \ll_{\delta^{\prime\prime\prime}} N_k(s_1,s_2) (2\pi)^{-(\sigma_1+\sigma_2)}|\Gamma(s_1)\Gamma(s_2)|k^{1-(\epsilon_2+\epsilon_1)+2\delta^{\prime\prime}}\dfrac{(4\pi)^k k^{\delta^{\prime\prime\prime}}}{\Gamma(k)}. \end{align*} $$
$$ \begin{align*} \sum_{f\in \mathcal{B}_k} \bigg\lvert\dfrac{L^*(f,s_1)L^*(f,s_2)}{\langle f,f \rangle}\bigg\rvert \ll_{\delta^{\prime\prime\prime}} N_k(s_1,s_2) (2\pi)^{-(\sigma_1+\sigma_2)}|\Gamma(s_1)\Gamma(s_2)|k^{1-(\epsilon_2+\epsilon_1)+2\delta^{\prime\prime}}\dfrac{(4\pi)^k k^{\delta^{\prime\prime\prime}}}{\Gamma(k)}. \end{align*} $$
We estimate
![]() ${\Gamma (s_2)}/{\Gamma (k-s_1)}$
by (4.1) to rewrite (8.1) as
${\Gamma (s_2)}/{\Gamma (k-s_1)}$
by (4.1) to rewrite (8.1) as
Thus, by first putting
![]() $\delta ^{\prime \prime \prime }=\delta ^{\prime \prime }$
and then replacing
$\delta ^{\prime \prime \prime }=\delta ^{\prime \prime }$
and then replacing
![]() $\delta ^{\prime \prime }$
by
$\delta ^{\prime \prime }$
by
![]() $\delta ^{\prime \prime }/3$
,
$\delta ^{\prime \prime }/3$
,
where the implied constant depends only on
![]() $T, \delta ^{\prime },\delta ^{\prime \prime }$
. Since
$T, \delta ^{\prime },\delta ^{\prime \prime }$
. Since
we conclude that there is a constant
![]() $C(T,\delta , \delta ^{\prime })>0$
such that, for
$C(T,\delta , \delta ^{\prime })>0$
such that, for
![]() $k \geq C(T,\delta , \delta ^{\prime })$
, the number of Hecke eigenforms in
$k \geq C(T,\delta , \delta ^{\prime })$
, the number of Hecke eigenforms in
![]() $S_k$
whose
$S_k$
whose
![]() $L^*$
-value is simultaneously nonvanishing at any two points
$L^*$
-value is simultaneously nonvanishing at any two points
![]() $s_1,s_2$
such that
$s_1,s_2$
such that
![]() $(s_1,s_2) \in R_{T,\delta ,\delta ^{\prime }}$
is at least
$(s_1,s_2) \in R_{T,\delta ,\delta ^{\prime }}$
is at least
![]() $k^{|\epsilon _1|+|\epsilon _2|-\delta ^{\prime \prime }}$
.
$k^{|\epsilon _1|+|\epsilon _2|-\delta ^{\prime \prime }}$
.
9 Proof of Corollary 3.5
Points on the (right) edge of the critical strip lie inside the known nonvanishing region of L-functions of Hecke eigenforms [Reference Moreno10], given by
 $$ \begin{align*} \mathrm{Re}(s) \geq \frac{k+1}{2} - \dfrac{c}{\log (k+|t|+3)}, \end{align*} $$
$$ \begin{align*} \mathrm{Re}(s) \geq \frac{k+1}{2} - \dfrac{c}{\log (k+|t|+3)}, \end{align*} $$
where
![]() $c>0$
is an absolute constant. By substituting
$c>0$
is an absolute constant. By substituting
![]() $s_2={(k+1)}/{2}$
in Corollary 3.4, we have
$s_2={(k+1)}/{2}$
in Corollary 3.4, we have
![]() $N_k(s_1) \gg _{T,\delta ^{\prime }, \delta ^{\prime \prime }} k^{1/2+|\epsilon _1|-\delta ^{\prime \prime }}$
for
$N_k(s_1) \gg _{T,\delta ^{\prime }, \delta ^{\prime \prime }} k^{1/2+|\epsilon _1|-\delta ^{\prime \prime }}$
for
![]() $k \gg _{T,\delta , \delta ^{\prime }} 1$
, when
$k \gg _{T,\delta , \delta ^{\prime }} 1$
, when
![]() $\delta \leq \epsilon _1 \leq \tfrac 12-\delta ^{\prime }$
.
$\delta \leq \epsilon _1 \leq \tfrac 12-\delta ^{\prime }$
.
Acknowledgements
The authors would like to thank Amir Akbary and Winfried Kohnen for their helpful comments on this paper. The third author thanks the Council of Scientific and Industrial Research (CSIR), Government of India, for its financial support.