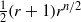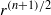Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
ZELENYUK, YEVHEN
and
ZELENYUK, YULIYA
2014.
COUNTING SYMMETRIC COLOURINGS OF THE VERTICES OF A REGULAR POLYGON.
Bulletin of the Australian Mathematical Society,
Vol. 90,
Issue. 1,
p.
1.
Bianconi, Francesco
and
González, Elena
2019.
Counting local n-ary patterns.
Pattern Recognition Letters,
Vol. 117,
Issue. ,
p.
24.
SINGH, SHIVANI
and
ZELENYUK, YULIYA
2019.
ALTERNATING COLOURINGS OF THE VERTICES OF A REGULAR POLYGON.
Bulletin of the Australian Mathematical Society,
Vol. 100,
Issue. 2,
p.
177.
Smeraldi, Fabrizio
Bianconi, Francesco
Fernández, Antonio
and
González, Elena
2020.
Partial Order Rank Features in Colour Space.
Applied Sciences,
Vol. 10,
Issue. 2,
p.
499.
Zelenyuk, Yuliya
2021.
Computing the number of symmetric colorings of elementary Abelian groups.
Alexandria Engineering Journal,
Vol. 60,
Issue. 2,
p.
2075.