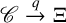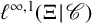1 Introduction
This article treats the symmetry of certain Banach
![]() $^*$
-algebras connected with Fell bundles over discrete groupoids. The study of symmetry for groupoid algebras started not long ago, with Austad and Ortega [Reference Austad and Ortega1]. They studied the Hahn algebra of a Hausdorff locally compact groupoid, gave necessary conditions for symmetry and even sufficient conditions in the case of transformation groupoids. This subject found a continuation in [Reference Flores, Jauré and Măntoiu2], where Jauré, Măntoiu and myself first treated the problem of symmetry for algebras related to Fell bundles over discrete groupoids. Among other things, in that paper, we proved a weaker form of Theorem 1.2 which is the main result of this paper.
$^*$
-algebras connected with Fell bundles over discrete groupoids. The study of symmetry for groupoid algebras started not long ago, with Austad and Ortega [Reference Austad and Ortega1]. They studied the Hahn algebra of a Hausdorff locally compact groupoid, gave necessary conditions for symmetry and even sufficient conditions in the case of transformation groupoids. This subject found a continuation in [Reference Flores, Jauré and Măntoiu2], where Jauré, Măntoiu and myself first treated the problem of symmetry for algebras related to Fell bundles over discrete groupoids. Among other things, in that paper, we proved a weaker form of Theorem 1.2 which is the main result of this paper.
Definition 1.1. A Banach
![]() $^*$
-algebra
$^*$
-algebra
![]() $\mathfrak B$
is called symmetric if the spectrum of
$\mathfrak B$
is called symmetric if the spectrum of
![]() $b^*b$
is positive for every
$b^*b$
is positive for every
![]() $b\in \mathfrak B$
(this happens if and only if the spectrum of any self-adjoint element is real).
$b\in \mathfrak B$
(this happens if and only if the spectrum of any self-adjoint element is real).
Theorem 1.2. Let
![]() $\Xi $
be a discrete groupoid. Then:
$\Xi $
be a discrete groupoid. Then:
-
(1) the algebra
 $\ell ^{\infty ,1}(\Xi )$
is symmetric if and only if every isotropy group of
$\ell ^{\infty ,1}(\Xi )$
is symmetric if and only if every isotropy group of
 $\Xi $
is symmetric;
$\Xi $
is symmetric; -
(2) the algebra
 $\ell ^{\infty ,1}(\Xi \!\mid \!\mathscr C)$
is symmetric for every Fell bundle
$\ell ^{\infty ,1}(\Xi \!\mid \!\mathscr C)$
is symmetric for every Fell bundle
 $\mathscr C$
over
$\mathscr C$
over
 $\Xi $
if and only if every isotropy group of
$\Xi $
if and only if every isotropy group of
 $\Xi $
is hypersymmetric.
$\Xi $
is hypersymmetric.
This result is interesting as it reduces the question of the (hyper)symmetry of a given groupoid to the (hyper)symmetry of its isotropy subgroups and the study of group
![]() $\ell ^1$
-algebras is far more developed. For example, see [Reference Austad and Ortega1, Reference Flores, Jauré and Măntoiu2, Reference Jauré and Măntoiu4, Reference Kugler5, Reference Leptin7–Reference Măntoiu10, Reference Poguntke13] and the references therein. Our results can be applied to get spectral
$\ell ^1$
-algebras is far more developed. For example, see [Reference Austad and Ortega1, Reference Flores, Jauré and Măntoiu2, Reference Jauré and Măntoiu4, Reference Kugler5, Reference Leptin7–Reference Măntoiu10, Reference Poguntke13] and the references therein. Our results can be applied to get spectral
![]() $^*$
-subalgebras of
$^*$
-subalgebras of
![]() $C^*$
-algebras associated with Fell bundles (a reduced Banach
$C^*$
-algebras associated with Fell bundles (a reduced Banach
![]() $^*$
-algebra is symmetric if and only if it is a spectral
$^*$
-algebra is symmetric if and only if it is a spectral
![]() $^*$
-subalgebra of its enveloping
$^*$
-subalgebra of its enveloping
![]() $C^*$
-algebra [Reference Palmer12, Theorem 11.4.1]).
$C^*$
-algebra [Reference Palmer12, Theorem 11.4.1]).
The article is divided into 3 parts. Section 2 deals with preliminaries, where we introduce Fell bundles, the Hahn algebra of a Fell bundle and define what (hyper)symmetry for a groupoid means. In Section 3, we introduce a characterisation for hypersymmetry using only Fell bundles with constant fibres. It is analogous to the characterisation made for groups by Jauré and Măntoiu in [Reference Jauré and Măntoiu4]. Finally, Section 4 deals with the proof of Theorem 1.2. This is achieved by writing a general discrete groupoid as a disjoint union of transitive groupoids and proving that transitive groupoids are isomorphic to transitive transformation groups. Using the available theory for groups yields the desired result.
2 Preliminaries
Let
![]() $\Xi $
be a groupoid, with unit space
$\Xi $
be a groupoid, with unit space
![]() $\mathcal U:=\Xi ^{(0)}$
, source map
$\mathcal U:=\Xi ^{(0)}$
, source map
![]() ${\mathrm {d}}$
and range map
${\mathrm {d}}$
and range map
![]() ${\mathrm {r}}$
. The
${\mathrm {r}}$
. The
![]() ${\mathrm {d}}$
- and
${\mathrm {d}}$
- and
![]() ${\mathrm {r}}$
-fibres are
${\mathrm {r}}$
-fibres are
![]() $\Xi _u=\{\xi \in \Xi \mid {\mathrm {d}}(\xi )=u\}$
and
$\Xi _u=\{\xi \in \Xi \mid {\mathrm {d}}(\xi )=u\}$
and
![]() $\Xi ^u=\{\xi \in \Xi \mid {\mathrm {r}}(\xi )=u\}$
. The set of composable pairs is
$\Xi ^u=\{\xi \in \Xi \mid {\mathrm {r}}(\xi )=u\}$
. The set of composable pairs is
The isotropy group associated with the unit
![]() $u\in \mathcal U$
is
$u\in \mathcal U$
is
![]() $\Xi _u^u=\Xi _u\cap \Xi ^u$
; it is a subgroupoid of
$\Xi _u^u=\Xi _u\cap \Xi ^u$
; it is a subgroupoid of
![]() $\Xi $
, which happens to be a group. We endow the groupoid
$\Xi $
, which happens to be a group. We endow the groupoid
![]() $\Xi $
with the discrete topology. Let us introduce an important class of groupoids which will be useful.
$\Xi $
with the discrete topology. Let us introduce an important class of groupoids which will be useful.
Definition 2.1. A groupoid
![]() $\Xi $
is called transitive if for any pair
$\Xi $
is called transitive if for any pair
![]() $u,v\in \mathcal U$
, there exists
$u,v\in \mathcal U$
, there exists
![]() $x\in \Xi $
such that
$x\in \Xi $
such that
![]() ${\mathrm {r}}(x)=u$
and
${\mathrm {r}}(x)=u$
and
![]() ${\mathrm {d}}(x)=v$
.
${\mathrm {d}}(x)=v$
.
The concept of transitivity is borrowed from the theory of dynamical systems. It comes from a natural but hidden action of the groupoid on its unit space. So the groupoid is transitive if and only if this action is transitive (see [Reference Flores and Măntoiu3, Example 2.2, Corollary 7.8]).
In this article, we are going to work with Fell bundles
![]() $\mathscr C\overset {q}{\to }\Xi $
over the groupoid
$\mathscr C\overset {q}{\to }\Xi $
over the groupoid
![]() ${\Xi }$
(see [Reference Kumjian6, Reference Muhly and Williams11]). A Fell bundle is composed of fibres such that each fibre
${\Xi }$
(see [Reference Kumjian6, Reference Muhly and Williams11]). A Fell bundle is composed of fibres such that each fibre
![]() $\mathfrak C _x\!:=q^{-1}(\{x\})$
is a Banach space with norm
$\mathfrak C _x\!:=q^{-1}(\{x\})$
is a Banach space with norm
![]() $\parallel \!\cdot \!\parallel _{\mathfrak C_x}$
, the topology of
$\parallel \!\cdot \!\parallel _{\mathfrak C_x}$
, the topology of
![]() $\mathscr C$
coincides with the norm topology on each fibre, there are antilinear continuous involutions
$\mathscr C$
coincides with the norm topology on each fibre, there are antilinear continuous involutions
and for all
![]() $(x,y)\in \Xi ^{(2)}$
, there are continuous multiplications
$(x,y)\in \Xi ^{(2)}$
, there are continuous multiplications
satisfying the following axioms valid for
![]() $a\in \mathfrak C_x, b\in \mathfrak C_y\,$
and
$a\in \mathfrak C_x, b\in \mathfrak C_y\,$
and
![]() $(x,y)\in \Xi ^{(2)}$
:
$(x,y)\in \Xi ^{(2)}$
:
-
•
 $\parallel \!ab\!\parallel _{\mathfrak C_{xy}}\,\le \,\parallel \!a\!\parallel _{\mathfrak C_{x}}\parallel \!b\!\parallel _{\mathfrak C_{y}}$
;
$\parallel \!ab\!\parallel _{\mathfrak C_{xy}}\,\le \,\parallel \!a\!\parallel _{\mathfrak C_{x}}\parallel \!b\!\parallel _{\mathfrak C_{y}}$
; -
•
 $(ab)^\bullet =b^\bullet a^\bullet $
;
$(ab)^\bullet =b^\bullet a^\bullet $
; -
•
 $\parallel \!a^\bullet a\!\parallel _{\mathfrak C_{{\mathrm {d}}(x)}}=\,\parallel \!a\!\parallel _{\mathfrak C_{x}}^2$
;
$\parallel \!a^\bullet a\!\parallel _{\mathfrak C_{{\mathrm {d}}(x)}}=\,\parallel \!a\!\parallel _{\mathfrak C_{x}}^2$
; -
•
 $a^\bullet a$
is positive in
$a^\bullet a$
is positive in
 $\mathfrak C_{{\mathrm {d}}(x)}$
.
$\mathfrak C_{{\mathrm {d}}(x)}$
.
From these axioms, it follows that
![]() $\mathfrak C _x$
is a
$\mathfrak C _x$
is a
![]() $C^*$
-algebra for every unit
$C^*$
-algebra for every unit
![]() $x\in \mathcal U$
. Sometimes we simply write
$x\in \mathcal U$
. Sometimes we simply write
![]() $\mathscr C=\bigsqcup _{x\in \Xi }\mathfrak C _x$
for the Fell bundle.
$\mathscr C=\bigsqcup _{x\in \Xi }\mathfrak C _x$
for the Fell bundle.
Our object of study is the Hahn algebra
![]() $\ell ^{\infty ,1}(\Xi \!\mid \!\mathscr C)$
adapted to Fell bundles [Reference Muhly and Williams11]. In our case, it is formed by the sections
$\ell ^{\infty ,1}(\Xi \!\mid \!\mathscr C)$
adapted to Fell bundles [Reference Muhly and Williams11]. In our case, it is formed by the sections
![]() $\Phi :\Xi \to \mathfrak C$
(thus satisfying
$\Phi :\Xi \to \mathfrak C$
(thus satisfying
![]() $\Phi (x)\in \mathfrak C_x$
for every
$\Phi (x)\in \mathfrak C_x$
for every
![]() $x\in \Xi $
) that can be obtained as a limit of finitely supported sections in the Hahn-type norm
$x\in \Xi $
) that can be obtained as a limit of finitely supported sections in the Hahn-type norm

It is a Banach
![]() $^*$
-algebra under the multiplication
$^*$
-algebra under the multiplication
 $$ \begin{align*} (\Phi* \Psi)(x):=\sum_{yz=x}\Phi(\,y)\bullet\Psi(z) \end{align*} $$
$$ \begin{align*} (\Phi* \Psi)(x):=\sum_{yz=x}\Phi(\,y)\bullet\Psi(z) \end{align*} $$
and the involution
Remark 2.2. Let us point out some properties of the functions in
![]() $\ell ^{\infty ,1}(\Xi \!\mid \!\mathscr C)$
. If
$\ell ^{\infty ,1}(\Xi \!\mid \!\mathscr C)$
. If
![]() $\Phi _n\in \ell ^{\infty ,1}(\Xi \!\mid \!\mathscr C)$
is a sequence of sections with finite support and
$\Phi _n\in \ell ^{\infty ,1}(\Xi \!\mid \!\mathscr C)$
is a sequence of sections with finite support and
![]() $\Phi _n\to \Phi $
, then the convergence is uniform. Indeed, let
$\Phi _n\to \Phi $
, then the convergence is uniform. Indeed, let
![]() $x\in \Xi $
and observe that
$x\in \Xi $
and observe that

So
. This implies that the function
![]() $\Phi $
has countable support and vanishes at
$\Phi $
has countable support and vanishes at
![]() $\infty $
.
$\infty $
.
We denote by
![]() $C^*(\Xi \,\vert \,\mathscr C)$
the enveloping
$C^*(\Xi \,\vert \,\mathscr C)$
the enveloping
![]() $C^*$
-algebra of the Hahn algebra
$C^*$
-algebra of the Hahn algebra
![]() $\ell ^{\infty ,1}(\Xi \!\mid \!\mathscr C)$
. It is a known fact that
$\ell ^{\infty ,1}(\Xi \!\mid \!\mathscr C)$
. It is a known fact that
![]() $\ell ^{\infty ,1}(\Xi \!\mid \!\mathscr C)$
is a dense
$\ell ^{\infty ,1}(\Xi \!\mid \!\mathscr C)$
is a dense
![]() $^*$
-subalgebra of
$^*$
-subalgebra of
![]() $C^*(\Xi \!\mid \!\mathscr C)$
.
$C^*(\Xi \!\mid \!\mathscr C)$
.
Definition 2.3
-
(i) The discrete groupoid
 $\Xi $
is called symmetric if the convolution Banach
$\Xi $
is called symmetric if the convolution Banach
 $^*$
-algebra
$^*$
-algebra
 $\ell ^{\infty ,1}(\Xi )$
is symmetric.
$\ell ^{\infty ,1}(\Xi )$
is symmetric. -
(ii) The discrete groupoid
 $\Xi $
is called hypersymmetric if given any Fell bundle
$\Xi $
is called hypersymmetric if given any Fell bundle
 $\mathscr C\!=\bigsqcup _{x\in \Xi }\mathfrak C _x$
, the Banach
$\mathscr C\!=\bigsqcup _{x\in \Xi }\mathfrak C _x$
, the Banach
 $^*$
-algebra
$^*$
-algebra
 $\ell ^{\infty ,1}(\Xi \!\mid \!\mathscr C)$
is symmetric.
$\ell ^{\infty ,1}(\Xi \!\mid \!\mathscr C)$
is symmetric.
Example 2.4. If
![]() $\Pi \subset X\times X$
is an equivalence relation on X, one can make
$\Pi \subset X\times X$
is an equivalence relation on X, one can make
![]() $\Xi =\Pi $
a discrete groupoid by defining the operations
$\Xi =\Pi $
a discrete groupoid by defining the operations
The unit space is
![]() $\,\mathcal U=\mathsf {Diag}(X)$
and it gets canonically identified with X, via the homeomorphism
$\,\mathcal U=\mathsf {Diag}(X)$
and it gets canonically identified with X, via the homeomorphism
![]() $(x,x)\mapsto x$
. In this case, all of the isotropy groups correspond to the trivial group
$(x,x)\mapsto x$
. In this case, all of the isotropy groups correspond to the trivial group
![]() $\Pi _u^u=\{(u,u)\}$
, so Theorem 4.9 will guarantee that
$\Pi _u^u=\{(u,u)\}$
, so Theorem 4.9 will guarantee that
![]() $\Pi $
is hypersymmetric. A particular example is the so called pair groupoid,
$\Pi $
is hypersymmetric. A particular example is the so called pair groupoid,
![]() $\Pi =X\times X$
.
$\Pi =X\times X$
.
3 A characterisation of hypersymmetry for discrete groupoids
In [Reference Flores, Jauré and Măntoiu2], we introduced some special Fell bundles arising from Hilbert bundles to characterise the hypersymmetry of a discrete groupoid. However, in this paper, we will improve this characterisation. One can actually verify hypersymmetry by looking at much simpler algebras associated to Fell bundles with constant fibres. Let us make precise the Fell bundles of interest.
Definition 3.1. By a (left) groupoid action of a discrete groupoid
![]() $\Xi $
on the
$\Xi $
on the
![]() $C^*$
-bundle
$C^*$
-bundle
![]() $\mathscr A\!:=\bigsqcup _{u\in \mathcal U}\mathfrak A_u\overset {p}{\to }\mathcal U$
over its unit space, we understand a continuous map
$\mathscr A\!:=\bigsqcup _{u\in \mathcal U}\mathfrak A_u\overset {p}{\to }\mathcal U$
over its unit space, we understand a continuous map
satisfying the axioms:
-
(a)
 $p[\mathcal T_x(\alpha )]={\mathrm {r}}(x)$
for all
$p[\mathcal T_x(\alpha )]={\mathrm {r}}(x)$
for all
 $x\in \Xi ,\,\alpha \in \mathfrak A_{{\mathrm {d}}(x)}$
;
$x\in \Xi ,\,\alpha \in \mathfrak A_{{\mathrm {d}}(x)}$
; -
(b) each
 $\mathcal T_x$
is a
$\mathcal T_x$
is a
 $^*$
-isomorphism
$^*$
-isomorphism
 $:\mathfrak A_{{\mathrm {d}}(x)}\!\to \mathfrak A_{{\mathrm {r}}(x)}$
;
$:\mathfrak A_{{\mathrm {d}}(x)}\!\to \mathfrak A_{{\mathrm {r}}(x)}$
; -
(c)
 $\mathcal T_u={\mathrm {id}}_{\mathfrak A_u}$
for all
$\mathcal T_u={\mathrm {id}}_{\mathfrak A_u}$
for all
 $u\in \mathcal U$
;
$u\in \mathcal U$
; -
(d) if
 $(x,y)\in \Xi ^{(2)}$
and
$(x,y)\in \Xi ^{(2)}$
and
 $(\alpha ,y)\in \mathscr A\rtimes \Xi $
, then
$(\alpha ,y)\in \mathscr A\rtimes \Xi $
, then
 $(\mathcal T_y(\alpha ),x)\in \mathscr A\rtimes \Xi $
and
$(\mathcal T_y(\alpha ),x)\in \mathscr A\rtimes \Xi $
and
 $\mathcal T_{xy}(\alpha )=\mathcal T_x[\mathcal T_y(\alpha )]$
.
$\mathcal T_{xy}(\alpha )=\mathcal T_x[\mathcal T_y(\alpha )]$
.
Definition 3.2. Let
![]() $\mathcal T$
be a groupoid action of
$\mathcal T$
be a groupoid action of
![]() $\Xi $
on the
$\Xi $
on the
![]() $C^*$
-bundle
$C^*$
-bundle
![]() $\mathscr A\!:=\bigsqcup _{u\in \mathcal U} \mathfrak A_u\overset {p}{\to }\mathcal U$
. We define its associated Fell bundle as follows. The underlying space is
$\mathscr A\!:=\bigsqcup _{u\in \mathcal U} \mathfrak A_u\overset {p}{\to }\mathcal U$
. We define its associated Fell bundle as follows. The underlying space is
![]() $\mathscr C_{\mathcal T}:=\mathscr A\rtimes \Xi $
with the topology inherited from the product topology and the obvious projection q. We endow it with the operations
$\mathscr C_{\mathcal T}:=\mathscr A\rtimes \Xi $
with the topology inherited from the product topology and the obvious projection q. We endow it with the operations
and
to get a Fell bundle over
![]() $\Xi $
. A section is now a map
$\Xi $
. A section is now a map
![]() $\Phi :\Xi \to \mathscr C_{\mathcal T}$
such that
$\Phi :\Xi \to \mathscr C_{\mathcal T}$
such that
So we may identify every section
![]() $\Phi \in \ell ^{\infty ,1}(\Xi \,\vert \,\mathscr C_{\mathcal T})$
with a function
$\Phi \in \ell ^{\infty ,1}(\Xi \,\vert \,\mathscr C_{\mathcal T})$
with a function
![]() $\Phi :\Xi \to \mathscr A$
(note the abuse of notation), such that
$\Phi :\Xi \to \mathscr A$
(note the abuse of notation), such that
![]() $ \Phi (x)\in \mathfrak A_{{{\mathrm {r}}}(x)}$
.
$ \Phi (x)\in \mathfrak A_{{{\mathrm {r}}}(x)}$
.
We will also denote the algebra
![]() $\ell ^{\infty ,1}(\Xi \,\vert \,\mathscr C_{\mathcal T})$
by
$\ell ^{\infty ,1}(\Xi \,\vert \,\mathscr C_{\mathcal T})$
by
![]() $\ell ^{\infty ,1}_{\mathcal T}(\Xi ,\mathscr A)$
to recall its particular nature. If the action
$\ell ^{\infty ,1}_{\mathcal T}(\Xi ,\mathscr A)$
to recall its particular nature. If the action
![]() $\mathcal T$
is trivial, meaning that
$\mathcal T$
is trivial, meaning that
![]() $\mathfrak A_u\equiv \mathfrak A$
for all
$\mathfrak A_u\equiv \mathfrak A$
for all
![]() $u\in \mathcal U$
and
$u\in \mathcal U$
and
![]() $\mathcal T_x\equiv {\mathrm {id}}_{\mathfrak A}$
for all
$\mathcal T_x\equiv {\mathrm {id}}_{\mathfrak A}$
for all
![]() $x\in \Xi $
, then we denote the resulting algebra simply by
$x\in \Xi $
, then we denote the resulting algebra simply by
![]() $\ell ^{\infty ,1}(\Xi ,\mathfrak A)$
.
$\ell ^{\infty ,1}(\Xi ,\mathfrak A)$
.
Remark 3.3. Let
![]() $\Phi ,\Psi \in \ell ^{\infty ,1}_{\mathcal T}(\Xi ,\mathscr A)$
. In this case, one may write the algebraic laws as
$\Phi ,\Psi \in \ell ^{\infty ,1}_{\mathcal T}(\Xi ,\mathscr A)$
. In this case, one may write the algebraic laws as
 $$ \begin{align*} [\Phi*\Psi](x) & =\!\sum_{y\in\Xi^{{\mathrm{r}}(x)}}\!\Phi(\,y)\mathcal T_y[\Psi(\,y^{-1}x)], \\ \Phi^*(x) & =\mathcal T_{x}[\Phi(x^{-1})]^* \end{align*} $$
$$ \begin{align*} [\Phi*\Psi](x) & =\!\sum_{y\in\Xi^{{\mathrm{r}}(x)}}\!\Phi(\,y)\mathcal T_y[\Psi(\,y^{-1}x)], \\ \Phi^*(x) & =\mathcal T_{x}[\Phi(x^{-1})]^* \end{align*} $$
and the Hahn-type norm as
 $$ \begin{align*} \parallel\!\Phi\!\parallel_{\ell^{\infty,1}_{\mathcal T}(\Xi,\mathscr A)}=\max\bigg\{\sup_{u\in \mathcal U}\sum_{{\mathrm{r}}(x)=u}\!\parallel\!\Phi(x)\!\parallel_{\mathfrak A_{{\mathrm{r}}(x)}},\,\sup_{u\in \mathcal U}\sum_{{\mathrm{d}}(x)=u}\!\parallel\!\Phi(x)\!\parallel_{\mathfrak A_{{\mathrm{r}}(x)}}\!\!\bigg\}. \end{align*} $$
$$ \begin{align*} \parallel\!\Phi\!\parallel_{\ell^{\infty,1}_{\mathcal T}(\Xi,\mathscr A)}=\max\bigg\{\sup_{u\in \mathcal U}\sum_{{\mathrm{r}}(x)=u}\!\parallel\!\Phi(x)\!\parallel_{\mathfrak A_{{\mathrm{r}}(x)}},\,\sup_{u\in \mathcal U}\sum_{{\mathrm{d}}(x)=u}\!\parallel\!\Phi(x)\!\parallel_{\mathfrak A_{{\mathrm{r}}(x)}}\!\!\bigg\}. \end{align*} $$
Lemma 3.4. Let
![]() $\mathscr C\!=\bigsqcup _{x\in \Xi }\mathfrak C_x$
be a Fell bundle over the discrete groupoid
$\mathscr C\!=\bigsqcup _{x\in \Xi }\mathfrak C_x$
be a Fell bundle over the discrete groupoid
![]() $\Xi $
. Then there exists an isometric
$\Xi $
. Then there exists an isometric
![]() $^*$
-monomorphism
$^*$
-monomorphism
Proof. Set
![]() $\mathfrak A:=C^*(\Xi \,\vert \,\mathscr C)$
and, for every
$\mathfrak A:=C^*(\Xi \,\vert \,\mathscr C)$
and, for every
![]() $x\in \Xi $
, embed
$x\in \Xi $
, embed
![]() $\mathfrak C_x$
into
$\mathfrak C_x$
into
![]() $\ell ^{\infty ,1}(\Xi \,\vert \,\mathscr C)\subset \mathfrak A$
by setting, for each
$\ell ^{\infty ,1}(\Xi \,\vert \,\mathscr C)\subset \mathfrak A$
by setting, for each
![]() $a\in \mathfrak C_x$
,
$a\in \mathfrak C_x$
,
It is not hard to prove that if
![]() $(x,y)\in \Xi ^{(2)}$
, then
$(x,y)\in \Xi ^{(2)}$
, then
hold. However, one also has
. For, if
![]() $x\in \mathcal U$
, this equality holds because
$x\in \mathcal U$
, this equality holds because
![]() $\theta _x:\mathfrak C_x\to \mathfrak A$
is a
$\theta _x:\mathfrak C_x\to \mathfrak A$
is a
![]() $^*$
-monomorphism of
$^*$
-monomorphism of
![]() $C^*$
-algebras and hence isometric, and if
$C^*$
-algebras and hence isometric, and if
![]() $x\in \Xi $
is not a unit, then one may apply the (now standard) trick
$x\in \Xi $
is not a unit, then one may apply the (now standard) trick
to conclude that
![]() $\theta _x$
preserves the mentioned norms. This allows us to successfully define
$\theta _x$
preserves the mentioned norms. This allows us to successfully define
and derive an isometry:

Now we check that
![]() $\varphi $
is a
$\varphi $
is a
![]() $^*$
-homomorphism,
$^*$
-homomorphism,
 $$ \begin{align*} [\varphi(\Phi)*\varphi(\Psi)](x)=\sum_{yz=x} \theta_y \Phi(\,y)*\theta_z\Psi(z) =\theta_x \sum_{yz=x} \Phi(\,y)\bullet\Psi(z) =\varphi(\Phi*\Psi)(x) \end{align*} $$
$$ \begin{align*} [\varphi(\Phi)*\varphi(\Psi)](x)=\sum_{yz=x} \theta_y \Phi(\,y)*\theta_z\Psi(z) =\theta_x \sum_{yz=x} \Phi(\,y)\bullet\Psi(z) =\varphi(\Phi*\Psi)(x) \end{align*} $$
and
This finishes the proof.
Remark 3.5. Observe that
![]() $\ell ^{\infty ,1}(\Xi ,\mathfrak A)\cong \ell ^{\infty ,1}(\Xi )\,\hat {\otimes }\,\mathfrak A$
, where
$\ell ^{\infty ,1}(\Xi ,\mathfrak A)\cong \ell ^{\infty ,1}(\Xi )\,\hat {\otimes }\,\mathfrak A$
, where
![]() $\hat {\otimes }$
denotes the projective tensor product. Indeed, given
$\hat {\otimes }$
denotes the projective tensor product. Indeed, given
![]() $(\varphi ,a)\in \ell ^{\infty ,1}(\Xi )\times \mathfrak A$
, define the function
$(\varphi ,a)\in \ell ^{\infty ,1}(\Xi )\times \mathfrak A$
, define the function
![]() $\varphi \otimes a$
by
$\varphi \otimes a$
by
The map
![]() $(\varphi ,a)\mapsto \varphi \otimes a$
defined in
$(\varphi ,a)\mapsto \varphi \otimes a$
defined in
![]() $\ell ^{\infty ,1}(\Xi )\times \mathfrak A\to \ell ^{\infty ,1}(\Xi ,\mathfrak A)$
is bilinear, has norm
$\ell ^{\infty ,1}(\Xi )\times \mathfrak A\to \ell ^{\infty ,1}(\Xi ,\mathfrak A)$
is bilinear, has norm
![]() $1$
(satisfies
$1$
(satisfies
![]() ) and it extends to a
) and it extends to a
![]() $^*$
-isomorphism
$^*$
-isomorphism
The following corollary effectively reduces our concerns to the study of tensor products, just as in the group case (see [Reference Jauré and Măntoiu4, Theorem 2.4]).
Corollary 3.6. A discrete groupoid
![]() $\Xi $
is hypersymmetric if and only if the Banach
$\Xi $
is hypersymmetric if and only if the Banach
![]() $^*$
-algebra
$^*$
-algebra
![]() $\ell ^{\infty ,1}(\Xi ,\mathfrak A)\cong \ell ^{\infty ,1}(\Xi )\,\hat {\otimes }\,\mathfrak A$
is symmetric for every
$\ell ^{\infty ,1}(\Xi ,\mathfrak A)\cong \ell ^{\infty ,1}(\Xi )\,\hat {\otimes }\,\mathfrak A$
is symmetric for every
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $\mathfrak A$
.
$\mathfrak A$
.
Proof. Every algebra of the form
![]() $\ell ^{\infty ,1}(\Xi ,\mathfrak A)$
comes from a Fell bundle (recall Definition 3.2), so it is symmetric if
$\ell ^{\infty ,1}(\Xi ,\mathfrak A)$
comes from a Fell bundle (recall Definition 3.2), so it is symmetric if
![]() $\Xi $
is hypersymmetric. However, because of Lemma 3.4, given any Fell bundle
$\Xi $
is hypersymmetric. However, because of Lemma 3.4, given any Fell bundle
![]() $\mathscr C$
, the algebra
$\mathscr C$
, the algebra
![]() $\ell ^{\infty ,1}(\Xi \,\vert \,\mathscr C)$
may be identified as a closed
$\ell ^{\infty ,1}(\Xi \,\vert \,\mathscr C)$
may be identified as a closed
![]() $^*$
-subalgebra of some algebra of the form
$^*$
-subalgebra of some algebra of the form
![]() $\ell ^{\infty ,1}(\Xi ,\mathfrak A)$
. So it will be symmetric if the latter is symmetric, by [Reference Palmer12, Theorem 11.4.2].
$\ell ^{\infty ,1}(\Xi ,\mathfrak A)$
. So it will be symmetric if the latter is symmetric, by [Reference Palmer12, Theorem 11.4.2].
Remark 3.7. In the group case, this condition has been called ‘rigid symmetry’ by many authors (including myself) and it was introduced by Leptin and Poguntke in [Reference Leptin and Poguntke9]. It can also be seen in [Reference Austad and Ortega1, Reference Flores, Jauré and Măntoiu2, Reference Jauré and Măntoiu4, Reference Măntoiu10, Reference Poguntke13].
Before going into the following sections, let us simplify some notation. Let
![]() $\mathfrak A,\mathfrak B$
be Banach
$\mathfrak A,\mathfrak B$
be Banach
![]() $^*$
-algebras. We will denote by
$^*$
-algebras. We will denote by
![]() $\mathfrak A\hookrightarrow \mathfrak B$
the fact that there exists an isometric
$\mathfrak A\hookrightarrow \mathfrak B$
the fact that there exists an isometric
![]() $^*$
-monomorphism
$^*$
-monomorphism
![]() $\iota :\mathfrak A\to \mathfrak B$
. In this language, the conclusion of Lemma 3.4 can be written as
$\iota :\mathfrak A\to \mathfrak B$
. In this language, the conclusion of Lemma 3.4 can be written as
![]() $\ell ^{\infty ,1}(\Xi \,\vert \,\mathscr C)\hookrightarrow \ell ^{\infty ,1}(\Xi ,C^*(\Xi \,\vert \,\mathscr C))$
. However, the dual notation
$\ell ^{\infty ,1}(\Xi \,\vert \,\mathscr C)\hookrightarrow \ell ^{\infty ,1}(\Xi ,C^*(\Xi \,\vert \,\mathscr C))$
. However, the dual notation
![]() $\mathfrak A\twoheadrightarrow \mathfrak B$
means that there exists some contractive
$\mathfrak A\twoheadrightarrow \mathfrak B$
means that there exists some contractive
![]() $^*$
-epimorphism
$^*$
-epimorphism
![]() $\pi :\mathfrak A\to \mathfrak B$
.
$\pi :\mathfrak A\to \mathfrak B$
.
4 The result for discrete groupoids
The rest of the paper is devoted to proving Theorem 4.9. We will follow the strategy detailed in the introduction, starting with a complete (well-known) characterisation of discrete transitive groupoids as group transformation groupoids.
Definition 4.1. Let
![]() $\gamma $
be a continuous action of the (discrete) group
$\gamma $
be a continuous action of the (discrete) group
![]() $\mathsf {G}$
on the topological space X. We define the transformation groupoid
$\mathsf {G}$
on the topological space X. We define the transformation groupoid
![]() $\Xi :=\mathsf {G}\ltimes _\gamma X$
associated to it as follows. As a topological space,
$\Xi :=\mathsf {G}\ltimes _\gamma X$
associated to it as follows. As a topological space,
![]() $\mathsf {G}\ltimes _\gamma X$
is just
$\mathsf {G}\ltimes _\gamma X$
is just
![]() $\mathsf {G}\times X$
and the maps
$\mathsf {G}\times X$
and the maps
![]() ${\mathrm {r}},{\mathrm {d}}$
are given by
${\mathrm {r}},{\mathrm {d}}$
are given by
![]() ${\mathrm {d}}(a,x)=x$
and
${\mathrm {d}}(a,x)=x$
and
![]() ${\mathrm {r}}(a,x)=\gamma _a(x)$
. The composition is
${\mathrm {r}}(a,x)=\gamma _a(x)$
. The composition is
![]() $(b,\gamma _a(x))(a,x):=(ba,x)$
and inversion reads
$(b,\gamma _a(x))(a,x):=(ba,x)$
and inversion reads
![]() $(a,x)^{-1}:=(a^{-1}\!,\gamma _a(x))$
. The unit space is
$(a,x)^{-1}:=(a^{-1}\!,\gamma _a(x))$
. The unit space is
![]() $\mathcal U=\{{\mathsf {e}}\}\times X\equiv X$
.
$\mathcal U=\{{\mathsf {e}}\}\times X\equiv X$
.
Proposition 4.2. Let
![]() $\Xi $
be a discrete transitive groupoid with isotropy group
$\Xi $
be a discrete transitive groupoid with isotropy group
![]() $\mathsf {G}$
. There is an abelian group structure on
$\mathsf {G}$
. There is an abelian group structure on
![]() $\mathcal U$
and an action
$\mathcal U$
and an action
![]() $\gamma $
of
$\gamma $
of
![]() $\mathsf {G}'=\mathsf {G}\times \mathcal U$
on
$\mathsf {G}'=\mathsf {G}\times \mathcal U$
on
![]() $\mathcal U$
such that
$\mathcal U$
such that
![]() $\Xi \cong \mathsf {G}'\ltimes _\gamma \mathcal U$
.
$\Xi \cong \mathsf {G}'\ltimes _\gamma \mathcal U$
.
Proof. Let us give
![]() $\mathcal U$
some abelian group structure with additive notation and define the action of
$\mathcal U$
some abelian group structure with additive notation and define the action of
![]() $\mathsf {G}'$
by
$\mathsf {G}'$
by
![]() $\gamma _{(\alpha ,w)}(v)=w+v$
. To construct an isomorphism
$\gamma _{(\alpha ,w)}(v)=w+v$
. To construct an isomorphism
![]() $\varphi $
, fix some
$\varphi $
, fix some
![]() $u\in \mathcal U$
and realise
$u\in \mathcal U$
and realise
![]() $\mathsf {G}$
as
$\mathsf {G}$
as
![]() $\Xi _u^u$
. Since
$\Xi _u^u$
. Since
![]() $\Xi $
is transitive, for every
$\Xi $
is transitive, for every
![]() $v\in \mathcal U$
, there exists an arrow
$v\in \mathcal U$
, there exists an arrow
![]() $z_v\in \Xi $
such that
$z_v\in \Xi $
such that
![]() ${\mathrm {d}}(z_v)=v$
and
${\mathrm {d}}(z_v)=v$
and
![]() ${\mathrm {r}}(z_v)=u$
. Then,
${\mathrm {r}}(z_v)=u$
. Then,
is the required isomorphism. Let us verify that
![]() $\varphi $
is indeed a groupoid isomorphism.
$\varphi $
is indeed a groupoid isomorphism.
-
(i) If
 $((x_1,w_1),w_2+v)((x_2,w_2),v)=((x_1x_2,w_1+w_2),v)$
, then
$((x_1,w_1),w_2+v)((x_2,w_2),v)=((x_1x_2,w_1+w_2),v)$
, then  $$ \begin{align*} \varphi((x_1x_2,w_1+w_2),v)&=z^{-1}_{w_1+w_2+v}x_1x_2z_{v} \\ &=z^{-1}_{w_1+w_2+v}x_1z_{w_2+v}z_{w_2+v}^{-1}x_2z_{v} \\ &=\varphi((x_1,w_1),w_2+v)\varphi((x_2,w_2),v). \end{align*} $$
$$ \begin{align*} \varphi((x_1x_2,w_1+w_2),v)&=z^{-1}_{w_1+w_2+v}x_1x_2z_{v} \\ &=z^{-1}_{w_1+w_2+v}x_1z_{w_2+v}z_{w_2+v}^{-1}x_2z_{v} \\ &=\varphi((x_1,w_1),w_2+v)\varphi((x_2,w_2),v). \end{align*} $$
-
(ii) If
 $((x,w),v)\in \mathsf {G}'\ltimes _\gamma \mathcal U$
, then
$((x,w),v)\in \mathsf {G}'\ltimes _\gamma \mathcal U$
, then
 $((x,w),v)^{-1}=((x^{-1},-w),w+v)$
and
$((x,w),v)^{-1}=((x^{-1},-w),w+v)$
and  $$ \begin{align*} \varphi((x^{-1},-w),w+v)=z^{-1}_v x^{-1}z_{w+v} =(z^{-1}_{w+v}x z_{v})^{-1}=\varphi((x,w),v)^{-1}. \end{align*} $$
$$ \begin{align*} \varphi((x^{-1},-w),w+v)=z^{-1}_v x^{-1}z_{w+v} =(z^{-1}_{w+v}x z_{v})^{-1}=\varphi((x,w),v)^{-1}. \end{align*} $$
-
(iii) The inverse function
 $\varphi ^{-1}$
is given by
$\varphi ^{-1}$
is given by
 $\varphi ^{-1}(\xi )=((z_{{\mathrm {r}}(\xi )}\xi z_{{\mathrm {d}}(\xi )}^{-1},{\mathrm {r}}(\xi )-{\mathrm {d}}(\xi )),{\mathrm {d}}(\xi )).\\[-33pt] $
$\varphi ^{-1}(\xi )=((z_{{\mathrm {r}}(\xi )}\xi z_{{\mathrm {d}}(\xi )}^{-1},{\mathrm {r}}(\xi )-{\mathrm {d}}(\xi )),{\mathrm {d}}(\xi )).\\[-33pt] $
Remark 4.3. It follows from Proposition 4.2 that the pair groupoid
![]() ${\mathcal U}\times {\mathcal U}$
is isomorphic to
${\mathcal U}\times {\mathcal U}$
is isomorphic to
![]() ${\mathcal U}\ltimes _{\gamma |_{\mathcal U}} {\mathcal U}$
. (Here,
${\mathcal U}\ltimes _{\gamma |_{\mathcal U}} {\mathcal U}$
. (Here,
![]() $\mathsf {G}=\{\mathsf {e}\}$
is the trivial group.)
$\mathsf {G}=\{\mathsf {e}\}$
is the trivial group.)
While the commutativity of
![]() $\mathcal U$
was not essential for the previous proof (any group structure would have worked out), it will be of vital importance in what follows (see the proof of Theorem 4.7). That is why it will be occasionally remarked in the following propositions.
$\mathcal U$
was not essential for the previous proof (any group structure would have worked out), it will be of vital importance in what follows (see the proof of Theorem 4.7). That is why it will be occasionally remarked in the following propositions.
The following lemma requires some notation. Given a
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $\mathfrak A$
and a group action
$\mathfrak A$
and a group action
![]() $\gamma :\mathsf {G}\to {\mathrm {Bij}}(\mathcal U)$
, denote by
$\gamma :\mathsf {G}\to {\mathrm {Bij}}(\mathcal U)$
, denote by
![]() $\Gamma $
the
$\Gamma $
the
![]() $\mathsf {G}$
-action on
$\mathsf {G}$
-action on
![]() $\mathcal C_0(\mathcal U,\mathfrak A)$
satisfying
$\mathcal C_0(\mathcal U,\mathfrak A)$
satisfying
![]() $\Gamma _x(\,f)(u)=f(\gamma _{x^{-1}}(u))$
.
$\Gamma _x(\,f)(u)=f(\gamma _{x^{-1}}(u))$
.
Lemma 4.4. Suppose that the discrete group
![]() $\mathsf {G}$
acts on
$\mathsf {G}$
acts on
![]() $\mathcal U$
via
$\mathcal U$
via
![]() $\gamma $
and
$\gamma $
and
![]() $\mathfrak A$
is a
$\mathfrak A$
is a
![]() $C^*$
-algebra. Then,
$C^*$
-algebra. Then,
Proof. Define
![]() $\pi :\ell ^1_\Gamma (\mathsf {G},\mathcal C_0(\mathcal U,\mathfrak A))\to \ell ^{\infty , 1}(\mathsf {G}\ltimes _\gamma \mathcal U,\mathfrak A)$
by the formula
$\pi :\ell ^1_\Gamma (\mathsf {G},\mathcal C_0(\mathcal U,\mathfrak A))\to \ell ^{\infty , 1}(\mathsf {G}\ltimes _\gamma \mathcal U,\mathfrak A)$
by the formula
![]() $\pi (\Phi )(x,u)=\Phi (x)(\gamma _{x}(u))$
. This map is well defined and clearly surjective, while it also satisfies
$\pi (\Phi )(x,u)=\Phi (x)(\gamma _{x}(u))$
. This map is well defined and clearly surjective, while it also satisfies

and
 $$ \begin{align*} \pi(\Phi*\Psi)(x,u)&=[\Phi*\Psi](x)(\gamma_{x}(u)) \\ &=\bigg[\sum_{y\in \mathsf{G}}\Phi(\,y)\Gamma_y[\Psi(\,y^{-1}x)]\bigg](\gamma_{x}(u)) \\ &=\sum_{y\in \mathsf{G}}\Phi(\,y)(\gamma_{x}(u))\Psi(\,y^{-1}x)(\gamma_{y^{-1}x}(u)) \\ &=\sum_{y\in \mathsf{G}}\pi(\Phi)(\,y,\gamma_{y^{-1}x}(u))\pi(\Psi)(\,y^{-1}x,u) \\ &=[\pi(\Phi)*\pi(\Psi)](x,u). \end{align*} $$
$$ \begin{align*} \pi(\Phi*\Psi)(x,u)&=[\Phi*\Psi](x)(\gamma_{x}(u)) \\ &=\bigg[\sum_{y\in \mathsf{G}}\Phi(\,y)\Gamma_y[\Psi(\,y^{-1}x)]\bigg](\gamma_{x}(u)) \\ &=\sum_{y\in \mathsf{G}}\Phi(\,y)(\gamma_{x}(u))\Psi(\,y^{-1}x)(\gamma_{y^{-1}x}(u)) \\ &=\sum_{y\in \mathsf{G}}\pi(\Phi)(\,y,\gamma_{y^{-1}x}(u))\pi(\Psi)(\,y^{-1}x,u) \\ &=[\pi(\Phi)*\pi(\Psi)](x,u). \end{align*} $$
Finally, we see that
 $$ \begin{align*} \pi(\Phi^*)(x,u)&=\Phi^*(x)(\gamma_{x}(u)) \\ &=\Gamma_x[\Phi(x^{-1})^*](\gamma_{x}(u))=\Phi(x^{-1})(u)^*=[\pi(\Phi)(x^{-1},\gamma_{x}(u))]^*=\pi(\Phi)^*(x,u). \end{align*} $$
$$ \begin{align*} \pi(\Phi^*)(x,u)&=\Phi^*(x)(\gamma_{x}(u)) \\ &=\Gamma_x[\Phi(x^{-1})^*](\gamma_{x}(u))=\Phi(x^{-1})(u)^*=[\pi(\Phi)(x^{-1},\gamma_{x}(u))]^*=\pi(\Phi)^*(x,u). \end{align*} $$
Hence,
![]() $\pi $
is a contractive
$\pi $
is a contractive
![]() $^*$
-epimorphism.
$^*$
-epimorphism.
Lemma 4.4 will be used in the following form, which allows us to focus on the study of
![]() $\ell ^1$
-algebras arising from group
$\ell ^1$
-algebras arising from group
![]() $C^*$
-dynamical systems.
$C^*$
-dynamical systems.
Corollary 4.5. If
![]() $\ell ^1_\Gamma (\mathsf {G},\mathcal C_0(\mathcal U,\mathfrak A))$
is a symmetric Banach
$\ell ^1_\Gamma (\mathsf {G},\mathcal C_0(\mathcal U,\mathfrak A))$
is a symmetric Banach
![]() $^*$
-algebra, then the algebra
$^*$
-algebra, then the algebra
![]() $\ell ^{\infty , 1}(\mathsf {G}\ltimes _\gamma \mathcal U,\mathfrak A)$
is also symmetric.
$\ell ^{\infty , 1}(\mathsf {G}\ltimes _\gamma \mathcal U,\mathfrak A)$
is also symmetric.
Proof. In Lemma 4.4, we showed that
![]() $\ell ^1_\Gamma (\mathsf {G},\mathcal C_0(\mathcal U,\mathfrak A))\twoheadrightarrow \ell ^{\infty , 1}(\mathsf {G}\ltimes _\gamma \mathcal U,\mathfrak A)$
, so the conclusion follows from [Reference Palmer12, Theorem 11.4.2].
$\ell ^1_\Gamma (\mathsf {G},\mathcal C_0(\mathcal U,\mathfrak A))\twoheadrightarrow \ell ^{\infty , 1}(\mathsf {G}\ltimes _\gamma \mathcal U,\mathfrak A)$
, so the conclusion follows from [Reference Palmer12, Theorem 11.4.2].
Proposition 4.6. Let
![]() $(\mathsf {G}\times \mathsf {H}, \Gamma , \mathfrak A)$
be a
$(\mathsf {G}\times \mathsf {H}, \Gamma , \mathfrak A)$
be a
![]() $C^*$
-dynamical system and assume that
$C^*$
-dynamical system and assume that
![]() $\mathsf {G}$
acts trivially on
$\mathsf {G}$
acts trivially on
![]() $\mathfrak A$
. Then one has
$\mathfrak A$
. Then one has
where
![]() $\mathsf {G}':=\mathsf {G}\times \mathsf {H}$
.
$\mathsf {G}':=\mathsf {G}\times \mathsf {H}$
.
Proof. Observe that
is an isometric
![]() $^*$
-isomorphism. Indeed, bijectivity is direct, while
$^*$
-isomorphism. Indeed, bijectivity is direct, while

and, identifying
![]() $(1_{\mathsf {G}},b)\in \mathsf {G}'$
with
$(1_{\mathsf {G}},b)\in \mathsf {G}'$
with
![]() $b\in \mathsf {H}$
,
$b\in \mathsf {H}$
,
 $$ \begin{align*} [\iota(\Phi)*\iota(\Psi)](x)(\,y)&=\bigg[ \sum_{a\in \mathsf{G}} \iota(\Phi)(a)*\iota(\Psi)(a^{-1}x)\bigg](\,y) \\ &=\sum_{a\in \mathsf{G}}\sum_{b\in \mathsf{H}} \iota(\Phi)(a)(b)\Gamma_{b}[\iota(\Psi)(a^{-1}x)(b^{-1}y)] \\ &=\sum_{(a,b)\in \mathsf{G}\times\mathsf{H}}\Phi(a,b){\Gamma}_{(a,b)}[\Psi(a^{-1}x,b^{-1}y)] \\ &=\iota(\Phi*\Psi)(x)(\,y). \end{align*} $$
$$ \begin{align*} [\iota(\Phi)*\iota(\Psi)](x)(\,y)&=\bigg[ \sum_{a\in \mathsf{G}} \iota(\Phi)(a)*\iota(\Psi)(a^{-1}x)\bigg](\,y) \\ &=\sum_{a\in \mathsf{G}}\sum_{b\in \mathsf{H}} \iota(\Phi)(a)(b)\Gamma_{b}[\iota(\Psi)(a^{-1}x)(b^{-1}y)] \\ &=\sum_{(a,b)\in \mathsf{G}\times\mathsf{H}}\Phi(a,b){\Gamma}_{(a,b)}[\Psi(a^{-1}x,b^{-1}y)] \\ &=\iota(\Phi*\Psi)(x)(\,y). \end{align*} $$
Finally,
So
![]() $\ell ^1_\Gamma (\mathsf {G}',\mathfrak A)\cong \ell ^1(\mathsf {G},\ell ^1_{\Gamma }(\mathsf {H},\mathfrak A))\cong \ell ^1(\mathsf {G})\,\hat {\otimes }\,\ell ^1_{\Gamma }(\mathsf {H},\mathfrak A)$
.
$\ell ^1_\Gamma (\mathsf {G}',\mathfrak A)\cong \ell ^1(\mathsf {G},\ell ^1_{\Gamma }(\mathsf {H},\mathfrak A))\cong \ell ^1(\mathsf {G})\,\hat {\otimes }\,\ell ^1_{\Gamma }(\mathsf {H},\mathfrak A)$
.
We can put together the previous lemmas to obtain the following result, which is Theorem 1.2 for transitive groupoids.
Theorem 4.7. Let
![]() $\Xi $
be a discrete transitive groupoid with isotropy subgroup
$\Xi $
be a discrete transitive groupoid with isotropy subgroup
![]() $\mathsf {G}$
. If
$\mathsf {G}$
. If
![]() $\mathsf {G}$
is symmetric (respectively hypersymmetric), then
$\mathsf {G}$
is symmetric (respectively hypersymmetric), then
![]() $\Xi $
is symmetric (respectively hypersymmetric).
$\Xi $
is symmetric (respectively hypersymmetric).
Proof. Let us divide the proof into two cases, the first one being about hypersymmetry. Because of Proposition 4.2, we may assume that
![]() $\Xi =\mathsf {G}'\ltimes _\gamma \mathsf {H}$
, with
$\Xi =\mathsf {G}'\ltimes _\gamma \mathsf {H}$
, with
![]() $\mathsf {G}'=\mathsf {G}\times \mathsf {H}$
and
$\mathsf {G}'=\mathsf {G}\times \mathsf {H}$
and
![]() $\gamma _{(g,h)}(k)=h+k$
.
$\gamma _{(g,h)}(k)=h+k$
.
First, suppose that
![]() $\mathsf {G}$
is hypersymmetric. Because of Corollaries 3.6 and 4.5, it is enough to show that
$\mathsf {G}$
is hypersymmetric. Because of Corollaries 3.6 and 4.5, it is enough to show that
![]() $\mathsf {G}\times \mathsf {H}$
is hypersymmetric (or ‘rigidly symmetric’, see Remark 3.7). However, this follows from the fact that
$\mathsf {G}\times \mathsf {H}$
is hypersymmetric (or ‘rigidly symmetric’, see Remark 3.7). However, this follows from the fact that
![]() $\mathsf {H}$
is abelian and [Reference Leptin and Poguntke9, Theorem 7].
$\mathsf {H}$
is abelian and [Reference Leptin and Poguntke9, Theorem 7].
Now suppose that
![]() $\mathsf {G}$
is only symmetric. Note that
$\mathsf {G}$
is only symmetric. Note that
![]() $\gamma |_{\mathsf {H}}$
coincides with the action of
$\gamma |_{\mathsf {H}}$
coincides with the action of
![]() $\mathsf {H}$
on itself by left translation, so we will denote it by
$\mathsf {H}$
on itself by left translation, so we will denote it by
![]() ${\mathrm {lt}}$
. Then,
${\mathrm {lt}}$
. Then,
 $$ \begin{align*} \ell^1_\Gamma(\mathsf{G}',\mathcal C_0(\mathsf{H}))&\overset{(\scriptsize 4.1)}{\cong} \ell^1(\mathsf{G})\,\hat{\otimes}\,\ell^1_{\mathrm{lt}}(\mathsf{H},\mathcal C_0(\mathsf{H})) \\ &\overset{(3.1)}{\hookrightarrow} \ell^1(\mathsf{G})\,\hat{\otimes}\,\ell^1(\mathsf{H})\,\hat{\otimes}\,(\mathsf{H}\ltimes_{\mathrm{lt}}\mathcal C_0(\mathsf{H})) \\ &\cong \ell^1(\mathsf{H})\,\hat{\otimes}\,\ell^1(\mathsf{G},\mathcal K(\ell^2(\mathsf{H}))). \end{align*} $$
$$ \begin{align*} \ell^1_\Gamma(\mathsf{G}',\mathcal C_0(\mathsf{H}))&\overset{(\scriptsize 4.1)}{\cong} \ell^1(\mathsf{G})\,\hat{\otimes}\,\ell^1_{\mathrm{lt}}(\mathsf{H},\mathcal C_0(\mathsf{H})) \\ &\overset{(3.1)}{\hookrightarrow} \ell^1(\mathsf{G})\,\hat{\otimes}\,\ell^1(\mathsf{H})\,\hat{\otimes}\,(\mathsf{H}\ltimes_{\mathrm{lt}}\mathcal C_0(\mathsf{H})) \\ &\cong \ell^1(\mathsf{H})\,\hat{\otimes}\,\ell^1(\mathsf{G},\mathcal K(\ell^2(\mathsf{H}))). \end{align*} $$
The final isomorphism holds because of the Stone–von Neumann theorem, that is,
![]() $\mathsf {H}\ltimes _{\mathrm {lt}}\kern-1.2pt \mathcal C_0(\mathsf {H})\kern-1.2pt\cong\kern-1.2pt \mathcal K(\ell ^2(\mathsf {H}))$
. Now,
$\mathsf {H}\ltimes _{\mathrm {lt}}\kern-1.2pt \mathcal C_0(\mathsf {H})\kern-1.2pt\cong\kern-1.2pt \mathcal K(\ell ^2(\mathsf {H}))$
. Now,
![]() $\ell ^1(\mathsf {G},\kern-1.2pt \mathcal K(\ell ^2(\mathsf {H})\kern-0.5pt)\kern-0.5pt)$
is symmetric because of [Reference Kugler5, Theorem 1], and hence
$\ell ^1(\mathsf {G},\kern-1.2pt \mathcal K(\ell ^2(\mathsf {H})\kern-0.5pt)\kern-0.5pt)$
is symmetric because of [Reference Kugler5, Theorem 1], and hence
![]() $\ell ^1(\mathsf {H})\,\hat {\otimes }\,\ell ^1(\mathsf {G},\mathcal K(\ell ^2(\mathsf {H})))$
is symmetric because of [Reference Leptin7, Theorem 5]. We conclude that
$\ell ^1(\mathsf {H})\,\hat {\otimes }\,\ell ^1(\mathsf {G},\mathcal K(\ell ^2(\mathsf {H})))$
is symmetric because of [Reference Leptin7, Theorem 5]. We conclude that
![]() $\ell ^1_\Gamma (\mathsf {G}',\mathcal C_0(\mathsf {H}))$
and thus
$\ell ^1_\Gamma (\mathsf {G}',\mathcal C_0(\mathsf {H}))$
and thus
![]() $\ell ^{\infty ,1}(\Xi )$
are symmetric.
$\ell ^{\infty ,1}(\Xi )$
are symmetric.
Corollary 4.8. The pair groupoid over a discrete set
![]() $\mathcal U$
is hypersymmetric.
$\mathcal U$
is hypersymmetric.
Now we will proceed to upgrade Theorem 4.7 to the case of general discrete groupoids.
Theorem 4.9. A discrete groupoid
![]() $\Xi $
is symmetric (respectively hypersymmetric) if and only if its isotropy subgroups are symmetric (respectively hypersymmetric).
$\Xi $
is symmetric (respectively hypersymmetric) if and only if its isotropy subgroups are symmetric (respectively hypersymmetric).
Proof. It is obvious that symmetry (respectively hypersymmetry) of
![]() $\Xi $
implies the symmetry (respectively hypersymmetry) of its isotropy groups (
$\Xi $
implies the symmetry (respectively hypersymmetry) of its isotropy groups (
![]() $\ell ^{1}(\Xi _u^u,\mathfrak A)\hookrightarrow \ell ^{\infty ,1}(\Xi ,\mathfrak A)$
in a natural way). As the ‘only if’ part is clear, let us prove the ‘if’ part.
$\ell ^{1}(\Xi _u^u,\mathfrak A)\hookrightarrow \ell ^{\infty ,1}(\Xi ,\mathfrak A)$
in a natural way). As the ‘only if’ part is clear, let us prove the ‘if’ part.
Let
![]() $\mathfrak A$
be a
$\mathfrak A$
be a
![]() $C^*$
-algebra and
$C^*$
-algebra and
![]() $\Phi $
be an arbitrary section in
$\Phi $
be an arbitrary section in
![]() $\ell ^{\infty ,1}(\Xi ,\mathfrak A)$
. The section
$\ell ^{\infty ,1}(\Xi ,\mathfrak A)$
. The section
![]() $\Phi $
has a countable support (see Remark 2.2) and, since every discrete groupoid can be decomposed as a disjoint union of discrete transitive subgroupoids, we can find a countable number of disjoint transitive subgroupoids
$\Phi $
has a countable support (see Remark 2.2) and, since every discrete groupoid can be decomposed as a disjoint union of discrete transitive subgroupoids, we can find a countable number of disjoint transitive subgroupoids
![]() $\{\Xi (i)\}_{i\in \mathbb {N}}$
, such that
$\{\Xi (i)\}_{i\in \mathbb {N}}$
, such that
![]() ${\mathrm {supp}}(\Phi )\subset \bigcup _{i=1}^\infty \Xi (i) $
. Define
${\mathrm {supp}}(\Phi )\subset \bigcup _{i=1}^\infty \Xi (i) $
. Define
![]() $\Phi _n\in \ell ^{\infty ,1}(\Xi ,\mathfrak A)$
by
$\Phi _n\in \ell ^{\infty ,1}(\Xi ,\mathfrak A)$
by
 $$ \begin{align*}\Phi_n(x):=\begin{cases} \Phi(x) & \text{if\ } x\in \bigcup_{i=1}^{n} \Xi(i) , \\ 0_{\mathfrak A} & \text{if\ } x\not\in \bigcup_{i=1}^{n} \Xi(i). \\ \end{cases}\end{align*} $$
$$ \begin{align*}\Phi_n(x):=\begin{cases} \Phi(x) & \text{if\ } x\in \bigcup_{i=1}^{n} \Xi(i) , \\ 0_{\mathfrak A} & \text{if\ } x\not\in \bigcup_{i=1}^{n} \Xi(i). \\ \end{cases}\end{align*} $$
Then,
![]() $\lim _n\Phi _n= \Phi $
in
$\lim _n\Phi _n= \Phi $
in
![]() $\ell ^{\infty ,1}(\Xi ,\mathfrak A)$
, but more importantly,
$\ell ^{\infty ,1}(\Xi ,\mathfrak A)$
, but more importantly,
 $$ \begin{align*} {\mathrm{Spec}}_{\ell^{\infty,1}(\Xi,\mathfrak A)}(\Phi)=\bigcup_{i=1}^\infty{\mathrm{Spec}}_{\ell^{\infty,1}(\Xi,\mathfrak A)}(\Phi_n). \end{align*} $$
$$ \begin{align*} {\mathrm{Spec}}_{\ell^{\infty,1}(\Xi,\mathfrak A)}(\Phi)=\bigcup_{i=1}^\infty{\mathrm{Spec}}_{\ell^{\infty,1}(\Xi,\mathfrak A)}(\Phi_n). \end{align*} $$
So, to conclude, it is enough to prove that
![]() ${\mathrm {Spec}}_{\ell ^{\infty ,1}(\Xi ,\mathfrak A)}(\Phi _n)\subset \mathbb {R}$
, whenever
${\mathrm {Spec}}_{\ell ^{\infty ,1}(\Xi ,\mathfrak A)}(\Phi _n)\subset \mathbb {R}$
, whenever
![]() $\Phi ^*=\Phi $
. Indeed, if
$\Phi ^*=\Phi $
. Indeed, if
![]() $\Phi ^*=\Phi $
, after fixing n, we see that
$\Phi ^*=\Phi $
, after fixing n, we see that
![]() $\Phi _n^*=\Phi _n$
and
$\Phi _n^*=\Phi _n$
and
![]() $\ell ^{\infty ,1}(\Xi ,\mathfrak A)$
contains an isometric
$\ell ^{\infty ,1}(\Xi ,\mathfrak A)$
contains an isometric
![]() $^*$
-isomorphic copy of
$^*$
-isomorphic copy of
![]() $\ell ^{\infty ,1}(\bigcup _{i=1}^n\Xi (i),\mathfrak A)$
, obtained by extending the sections in the latter algebra with zeros outside its original domain. So by definition, one has
$\ell ^{\infty ,1}(\bigcup _{i=1}^n\Xi (i),\mathfrak A)$
, obtained by extending the sections in the latter algebra with zeros outside its original domain. So by definition, one has
![]() $\Phi _n\in \ell ^{\infty ,1}(\bigcup _{i=1}^n\Xi (i),\mathfrak A) \subset \ell ^{\infty ,1}(\Xi ,\mathfrak A)$
, which implies that
$\Phi _n\in \ell ^{\infty ,1}(\bigcup _{i=1}^n\Xi (i),\mathfrak A) \subset \ell ^{\infty ,1}(\Xi ,\mathfrak A)$
, which implies that
However,
![]() $\ell ^{\infty ,1}(\bigcup _{i=1}^n\Xi (i),\mathfrak A)\cong \bigoplus _{i=1}^n \ell ^{\infty ,1}(\Xi (i),\mathfrak A)$
and since the (finite) direct sum of symmetric Banach
$\ell ^{\infty ,1}(\bigcup _{i=1}^n\Xi (i),\mathfrak A)\cong \bigoplus _{i=1}^n \ell ^{\infty ,1}(\Xi (i),\mathfrak A)$
and since the (finite) direct sum of symmetric Banach
![]() $^*$
-algebras is symmetric,
$^*$
-algebras is symmetric,
![]() ${\mathrm {Spec}}_{\ell ^{\infty ,1}(\bigcup _{i=1}^n\Xi (i),\mathfrak A)}(\Phi _n)\subset \mathbb {R}$
and the result follows.
${\mathrm {Spec}}_{\ell ^{\infty ,1}(\bigcup _{i=1}^n\Xi (i),\mathfrak A)}(\Phi _n)\subset \mathbb {R}$
and the result follows.
Example 4.10. Let
![]() $\Xi =\mathsf {G}\ltimes _\gamma X$
be a transformation groupoid (see Definition 4.1), where X is discrete. In this case,
$\Xi =\mathsf {G}\ltimes _\gamma X$
be a transformation groupoid (see Definition 4.1), where X is discrete. In this case,
![]() $\mathcal U=X$
and
$\mathcal U=X$
and
![]() $\Xi _u^u=\{g\in G\mid \gamma _g(u)=u\}\times \{u\}$
, which can be identified with the stabiliser of u, namely
$\Xi _u^u=\{g\in G\mid \gamma _g(u)=u\}\times \{u\}$
, which can be identified with the stabiliser of u, namely
![]() ${\mathrm {Stab}}_\gamma (u)\leq \mathsf {G}$
.
${\mathrm {Stab}}_\gamma (u)\leq \mathsf {G}$
.
Remark 4.11. We will finish this paper with a bit of wishful thinking. It is reasonable to believe that the groupoid analogue of [Reference Flores, Jauré and Măntoiu2, Theorem 3.3] could be true. For a general locally compact groupoid, one can define symmetry and hypersymmetry for
![]() $\Xi $
as the symmetry of the Hahn algebras
$\Xi $
as the symmetry of the Hahn algebras
![]() $L^{\infty ,1}(\Xi )$
and
$L^{\infty ,1}(\Xi )$
and
![]() $L^{\infty ,1}(\Xi \!\mid \!\mathscr C)$
, respectively. So we may pose two problems.
$L^{\infty ,1}(\Xi \!\mid \!\mathscr C)$
, respectively. So we may pose two problems.
-
(i) Is the (hyper)symmetry of a Hausdorff locally compact groupoid
 $\Xi $
implied by the (hyper)symmetry of its discretisation
$\Xi $
implied by the (hyper)symmetry of its discretisation
 $\Xi ^{\mathrm {dis}}$
?
$\Xi ^{\mathrm {dis}}$
? -
(ii) Is Corollary 3.6 still valid for étale groupoids?
In view of Theorem 1.2, problem (i) is equivalent to the following.
-
(i′) Is the (hyper)symmetry of a Hausdorff locally compact groupoid
 $\Xi $
implied by the (hyper)symmetry of its discretised isotropy groups
$\Xi $
implied by the (hyper)symmetry of its discretised isotropy groups
 $(\Xi _u^u)^{\mathrm {dis}}$
?
$(\Xi _u^u)^{\mathrm {dis}}$
?