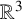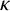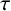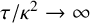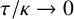1 Introduction
Curve shortening flow is the geometric flow defined by the equation
where
![]() $\gamma $
is a smooth immersed curve in
$\gamma $
is a smooth immersed curve in
![]() $\mathbb {R}^n$
,
$\mathbb {R}^n$
,
![]() $\kappa $
is the curvature and N is the unit normal vector. Solutions to this flow consist of a family of curves
$\kappa $
is the curvature and N is the unit normal vector. Solutions to this flow consist of a family of curves
![]() $\gamma _t$
for
$\gamma _t$
for
![]() $t \in [0,~\omega )$
with
$t \in [0,~\omega )$
with
![]() $\gamma _0$
(which we will often denote as
$\gamma _0$
(which we will often denote as
![]() $\gamma $
) as the initial condition.
$\gamma $
) as the initial condition.
This flow was introduced by Gage and Hamilton in 1986 as the
![]() $L^2$
gradient flow for the arc length (that is, the flow which shortens curves the quickest) [Reference Gage and Hamilton5]. Their work established short-time existence and uniqueness for the flow and showed that if one starts with a closed convex curve in the plane, the curve shrinks to a point while becoming asymptotically round. Put succinctly, convex curves shrink to round points. The following year, Grayson [Reference Grayson6] proved that any curve which is initially embedded (that is, does not self-intersect) in
$L^2$
gradient flow for the arc length (that is, the flow which shortens curves the quickest) [Reference Gage and Hamilton5]. Their work established short-time existence and uniqueness for the flow and showed that if one starts with a closed convex curve in the plane, the curve shrinks to a point while becoming asymptotically round. Put succinctly, convex curves shrink to round points. The following year, Grayson [Reference Grayson6] proved that any curve which is initially embedded (that is, does not self-intersect) in
![]() $\mathbb {R}^2$
eventually becomes convex under the flow, and thus converges to a round point.
$\mathbb {R}^2$
eventually becomes convex under the flow, and thus converges to a round point.
In two dimensions, curve shortening flow has two fundamental properties which play a crucial role in its analysis. First, if a curve starts as an embedded curve, it remains embedded and does not self-intersect until it reaches a singularity. More generally, if one considers mean-curvature flow for co-dimension one hypersurfaces, the flow is self-avoiding. In other words, surfaces that do not intersect at the initial time will never intersect in the future. Second, the number of inflection points (that is, points where the curvature changes signs) is nonincreasing under the flow. Both of these facts can be shown by a straightforward application of the parabolic maximum principle but fail for curve shortening flow in higher dimensions.
1.1 Singularity formation
Since curve shortening flow shrinks the length of curves as quickly as possible in the
![]() $L^2$
topology, a closed curve must encounter a singularity at some time
$L^2$
topology, a closed curve must encounter a singularity at some time
![]() $\omega $
. For closed and embedded curves in the plane, the enclosed area decreases linearly at the rate of
$\omega $
. For closed and embedded curves in the plane, the enclosed area decreases linearly at the rate of
![]() $-2 \pi $
, so it is possible to compute this time explicitly. The singularities are fairly well understood in two dimensions and a natural question is to extend these results to curve shortening flow in dimensions three or higher. To discuss this further, we first introduce some notation.
$-2 \pi $
, so it is possible to compute this time explicitly. The singularities are fairly well understood in two dimensions and a natural question is to extend these results to curve shortening flow in dimensions three or higher. To discuss this further, we first introduce some notation.
Curve shortening flow exists so long as the curvature is bounded. So to study singularities, we consider a blow-up sequence, which is a sequence of points in space-time
![]() $(p_m, t_m)$
such that the curvature at
$(p_m, t_m)$
such that the curvature at
![]() $(p_m, t_m)$
goes to infinity. A blow-up sequence is said to be essential if
$(p_m, t_m)$
goes to infinity. A blow-up sequence is said to be essential if
![]() $\kappa ^2(p_m, t_m) \ge \rho M_{t_m}$
for some
$\kappa ^2(p_m, t_m) \ge \rho M_{t_m}$
for some
![]() $\rho> 0$
where
$\rho> 0$
where
One can divide the singularities of curve shortening flow into two broad classes: Type I and Type II. A singularity is said to be Type I if
is bounded and Type II otherwise. Type-I singularities are global singularities, in that the entire curve shrinks to a point while converging in
![]() $C^\infty $
to a homothetic (that is, self-similar) shrinking curve. For closed curves in two dimensions, the possible models for these singularities were classified by Abresch and Langer [Reference Abresch and Langer1]. However, Type-II singularities are local in that the curvature goes to infinity in a small region while possibly remaining bounded elsewhere. Such singularities appear as kinks in the curve. In particular, they admit an essential blow-up sequence which (after rescaling) converges in
$C^\infty $
to a homothetic (that is, self-similar) shrinking curve. For closed curves in two dimensions, the possible models for these singularities were classified by Abresch and Langer [Reference Abresch and Langer1]. However, Type-II singularities are local in that the curvature goes to infinity in a small region while possibly remaining bounded elsewhere. Such singularities appear as kinks in the curve. In particular, they admit an essential blow-up sequence which (after rescaling) converges in
![]() $C^\infty $
to the Grim Reaper curve
$C^\infty $
to the Grim Reaper curve
![]() $y = -\log (\cos x)$
, which is a translating soliton under the flow.
$y = -\log (\cos x)$
, which is a translating soliton under the flow.
As we have mentioned, curve shortening flow behaves differently in higher dimensions, which complicates its analysis. However, Altschuler [Reference Altschuler2] established that under the flow, curves in three-dimensional space become asymptotically planar near any singularity. More precisely, along any essential blow-up sequence
![]() $(p_m,t_m)$
, the torsion
$(p_m,t_m)$
, the torsion
![]() $\tau $
satisfies
$\tau $
satisfies
This result was then extended to curve shortening flow in
![]() $\mathbb {R}^n$
by Yan and Jiao [Reference Yang and Jiao11]. As such, the singularity models for curve shortening flow in higher dimensions are the same as for curve shortening flow in the plane, although we cannot rule out the appearance of Abresch–Langer solutions (possibly covered multiple times) or Type-II singularities even when the initial curve is embedded.
$\mathbb {R}^n$
by Yan and Jiao [Reference Yang and Jiao11]. As such, the singularity models for curve shortening flow in higher dimensions are the same as for curve shortening flow in the plane, although we cannot rule out the appearance of Abresch–Langer solutions (possibly covered multiple times) or Type-II singularities even when the initial curve is embedded.
2 Twisted curves and the curvature-torsion entropy
A curve in
![]() $\mathbb {R}^n$
is said to be twisted if it has linearly independent derivatives up to order n [Reference Costa4]. In three dimensions, this corresponds to the nowhere vanishing of the curvature and torsion along the curve. As an archetypal example, one can consider a curve which wraps tightly around a torus, as shown in Figure 1.
$\mathbb {R}^n$
is said to be twisted if it has linearly independent derivatives up to order n [Reference Costa4]. In three dimensions, this corresponds to the nowhere vanishing of the curvature and torsion along the curve. As an archetypal example, one can consider a curve which wraps tightly around a torus, as shown in Figure 1.

Figure 1 An example of a twisted curve.
The main focus of this paper is to study curve shortening flow for twisted curves (that is, curves that are twisted). In particular, we focus on the possible singularities which emerge when a curve is twisted.
Theorem 2.1. Suppose
![]() $\gamma _t$
is a solution to curve shortening flow which is twisted up to the time of singularity
$\gamma _t$
is a solution to curve shortening flow which is twisted up to the time of singularity
![]() $\omega $
. Then:
$\omega $
. Then:
-
(1) the singularity is Type II;
-
(2) there exists a sequence
 $(p_m,t_m)$
so that
$(p_m,t_m)$
so that
 $t_m \to \omega $
and
$t_m \to \omega $
and  $$ \begin{align*} \frac{\tau}{\kappa^2}(p_m,t_m) \to \infty. \end{align*} $$
$$ \begin{align*} \frac{\tau}{\kappa^2}(p_m,t_m) \to \infty. \end{align*} $$
Note that the sequences where
![]() ${\tau }/{\kappa ^2} \to \infty $
cannot be essential, and may not even be a blow-up sequence at all. To establish this fact, we find a quantity that is (nearly) increasing under the flow. In particular, we will study the following entropy functional, whose behaviour is well controlled under the flow.
${\tau }/{\kappa ^2} \to \infty $
cannot be essential, and may not even be a blow-up sequence at all. To establish this fact, we find a quantity that is (nearly) increasing under the flow. In particular, we will study the following entropy functional, whose behaviour is well controlled under the flow.
Definition 2.2. For a twisted curve in
![]() $\mathbb {R}^3$
, the curvature-torsion entropy is defined to be the quantity
$\mathbb {R}^3$
, the curvature-torsion entropy is defined to be the quantity
 $$ \begin{align} \int_\gamma \kappa \log\bigg( \frac{\tau}{\kappa^2} \bigg) \, ds. \end{align} $$
$$ \begin{align} \int_\gamma \kappa \log\bigg( \frac{\tau}{\kappa^2} \bigg) \, ds. \end{align} $$
One could extend this definition to nontwisted curves by squaring the argument of the logarithm. However, this integral will essentially always be
![]() $-\infty $
whenever there is a flat point (that is, a point with
$-\infty $
whenever there is a flat point (that is, a point with
![]() $\tau =0$
), so we will not consider this generalisation.
$\tau =0$
), so we will not consider this generalisation.
3 Nearly monotonic functionals
To prove the main result, we must show that the curvature-torsion entropy is nearly nondecreasing under the flow. Before doing so, we start with a simpler proof that a twisted curve cannot develop a Type-I singularity. This result was previously shown in unpublished work of the author [Reference Khan7]. Since the proof is very short, we include it here.
Theorem 3.1. Suppose
![]() $\gamma $
is a twisted curve in
$\gamma $
is a twisted curve in
![]() $\mathbb {R}^3$
. Under curve shortening flow, one of the following two possibilities occurs.
$\mathbb {R}^3$
. Under curve shortening flow, one of the following two possibilities occurs.
-
(1) There exists a time
 $t_0$
where
$t_0$
where
 $\gamma _{t_0}$
has a point with vanishing curvature. Furthermore, after this time,
$\gamma _{t_0}$
has a point with vanishing curvature. Furthermore, after this time,
 $\gamma _t$
has a flat point until the singular time.
$\gamma _t$
has a flat point until the singular time. -
(2)
 $\gamma _t$
develops a Type-II singularity.
$\gamma _t$
develops a Type-II singularity.
Proof. Consider any curve
![]() $\gamma $
(not necessarily twisted) which develops a Type-I singularity at time
$\gamma $
(not necessarily twisted) which develops a Type-I singularity at time
![]() $\omega $
. After rescaling,
$\omega $
. After rescaling,
![]() $\gamma _t$
approaches an Abresch–Langer solution [Reference Abresch and Langer1] with finite winding number in the
$\gamma _t$
approaches an Abresch–Langer solution [Reference Abresch and Langer1] with finite winding number in the
![]() $C^\infty $
sense [Reference Altschuler2]. This has two consequences.
$C^\infty $
sense [Reference Altschuler2]. This has two consequences.
(a) All blow-up sequences are essential. In other words, for times close to the singularity, the maximum curvature is a bounded multiple of the minimum curvature. As a result, there exists a time
![]() $t_0 \in [0, \omega )$
such that for all times afterward,
$t_0 \in [0, \omega )$
such that for all times afterward,
![]() $\gamma _t$
has no inflection points, which implies that torsion is defined everywhere on the curve.
$\gamma _t$
has no inflection points, which implies that torsion is defined everywhere on the curve.
(b) Since
![]() $\gamma $
converges to some Abresch–Langer curve, the functional
$\gamma $
converges to some Abresch–Langer curve, the functional
![]() $D(t) = \sup \kappa _t \cdot L_t$
converges to a finite limit as the time goes to
$D(t) = \sup \kappa _t \cdot L_t$
converges to a finite limit as the time goes to
![]() $\omega $
, where
$\omega $
, where
![]() $L_t$
is the length of the curve. In particular, this quantity remains bounded.
$L_t$
is the length of the curve. In particular, this quantity remains bounded.
Now we consider a solution
![]() $\gamma _t$
which is twisted after
$\gamma _t$
which is twisted after
![]() $t_0$
. For the following calculations, we parametrise
$t_0$
. For the following calculations, we parametrise
![]() $\gamma _t$
smoothly by
$\gamma _t$
smoothly by
![]() $u \in [0, 2\pi )$
and suppose that the curvature has velocity v. To establish the result, we show that for a twisted curve, the total torsion is increasing:
$u \in [0, 2\pi )$
and suppose that the curvature has velocity v. To establish the result, we show that for a twisted curve, the total torsion is increasing:
 $$ \begin{align*} \int_{\gamma_t} \tau \, ds = \int_0^{2\pi} \tau \cdot v \, du. \end{align*} $$
$$ \begin{align*} \int_{\gamma_t} \tau \, ds = \int_0^{2\pi} \tau \cdot v \, du. \end{align*} $$
To compute the evolution of this quantity, we use the evolution equations for v,
![]() $\kappa $
and
$\kappa $
and
![]() $\tau $
(derived in [Reference Altschuler2, Reference Altschuler and Grayson3]):
$\tau $
(derived in [Reference Altschuler2, Reference Altschuler and Grayson3]):
 $$ \begin{align} \partial_t v & = -\kappa^2 v; \nonumber \\ \partial_t \kappa &= \partial_s^2 \kappa + \kappa^3 -\kappa\tau^2; \\ \partial_t \tau&= 2\kappa^2\tau + \partial_s \bigg(\frac{2\tau}{\kappa} \partial_s \kappa \bigg) + \partial_s^2 \tau. \nonumber \end{align} $$
$$ \begin{align} \partial_t v & = -\kappa^2 v; \nonumber \\ \partial_t \kappa &= \partial_s^2 \kappa + \kappa^3 -\kappa\tau^2; \\ \partial_t \tau&= 2\kappa^2\tau + \partial_s \bigg(\frac{2\tau}{\kappa} \partial_s \kappa \bigg) + \partial_s^2 \tau. \nonumber \end{align} $$
Using these, we find
 $$ \begin{align*} \partial_t \int_{\gamma_t} \tau\cdot v \, du & = \int_0^{2\pi} (\partial_t \tau) \cdot v + (\partial_t v) \cdot \tau \, du\\ & = \int_0^{2\pi} \bigg( 2\kappa^2\tau + \partial_s \bigg(\frac{2\tau}{\kappa} \partial_s \kappa \bigg) + \partial_s^2 \tau \bigg) v -\kappa^2 v \tau \, du\\ & = \int_{\gamma_t} \kappa^2 \tau \, ds + \int_\gamma \partial_s \bigg(\frac{2\tau}{\kappa} \partial_s \kappa \bigg) + \partial_s^2 \tau \, ds \\ & = \int_{\gamma_t} \kappa^2 \tau \, ds. \end{align*} $$
$$ \begin{align*} \partial_t \int_{\gamma_t} \tau\cdot v \, du & = \int_0^{2\pi} (\partial_t \tau) \cdot v + (\partial_t v) \cdot \tau \, du\\ & = \int_0^{2\pi} \bigg( 2\kappa^2\tau + \partial_s \bigg(\frac{2\tau}{\kappa} \partial_s \kappa \bigg) + \partial_s^2 \tau \bigg) v -\kappa^2 v \tau \, du\\ & = \int_{\gamma_t} \kappa^2 \tau \, ds + \int_\gamma \partial_s \bigg(\frac{2\tau}{\kappa} \partial_s \kappa \bigg) + \partial_s^2 \tau \, ds \\ & = \int_{\gamma_t} \kappa^2 \tau \, ds. \end{align*} $$
Therefore, the
![]() $L^1$
norm of
$L^1$
norm of
![]() $\tau $
is increasing and approaches a positive (possibly infinite) limit as t goes to
$\tau $
is increasing and approaches a positive (possibly infinite) limit as t goes to
![]() $\omega $
. However,
$\omega $
. However,
When combined with the fact that
![]() $D(t)$
remains bounded, this implies that
$D(t)$
remains bounded, this implies that
which contradicts the planarity theorem. As a result, the curve must develop a Type-II singularity. To complete the proof, we show that if a curve is twisted, it cannot become untwisted unless a point of zero curvature appears.
Proposition 3.2. Suppose we have a family of curves
![]() $\gamma _t$
in
$\gamma _t$
in
![]() ${\mathbb {R}}^3$
which satisfy (1.1) and that
${\mathbb {R}}^3$
which satisfy (1.1) and that
![]() $\gamma _0$
is twisted. Furthermore, suppose that
$\gamma _0$
is twisted. Furthermore, suppose that
![]() $\gamma _t$
has no inflection points for
$\gamma _t$
has no inflection points for
![]() $t\in [0,t_0]$
. Then for all
$t\in [0,t_0]$
. Then for all
![]() $t\in [0,t_0]$
,
$t\in [0,t_0]$
,
![]() $\gamma _t$
is also twisted.
$\gamma _t$
is also twisted.
This proposition follows from the maximum principle. Suppose that we have a point
![]() $(p,t)$
so that
$(p,t)$
so that
![]() $\tau (p,t)=0$
and this is the first time when
$\tau (p,t)=0$
and this is the first time when
![]() $\tau $
is ever nonpositive. Since both
$\tau $
is ever nonpositive. Since both
![]() $\tau $
and
$\tau $
and
![]() $\partial _s \tau $
are zero,
$\partial _s \tau $
are zero,
By the strong parabolic maximum principle,
![]() $\tau $
must remain strictly positive.
$\tau $
must remain strictly positive.
This argument fails at inflection points, where torsion is not defined. As such, this result shows that for a Type-I singularity to develop from a twisted curve, an inflection point must emerge and, afterward, a flat point is created where the inflection point occurred. It might seem curious that a single flat point will emerge as we initially expect the torsion to switch signs twice. However, the Frenet–Serret frame bundle can become nontrivial after the emergence of an inflection point.
3.1 The main result
We now turn our attention to proving the main result. To begin, we compute several more time derivatives:
 $$ \begin{align} \partial_t \int_{\gamma_t} \kappa \,ds &= - \int_{\gamma_t} \kappa \tau^2 \, ds\nonumber \\\kern-20pt \partial_t \int_{\gamma_t} \kappa \log \kappa \,ds & = \int_{\gamma_t} (\log \kappa+1) (\partial_s^2 \kappa +\kappa^3-\kappa \tau^2) - \kappa^3 \log \kappa\, ds\nonumber \\\kern-20pt & = \int_{\gamma_t} -\frac{(\partial_s \kappa)^2}{\kappa} - (\kappa \log \kappa) \tau^2 + \kappa^3 - \kappa \tau^2 \, ds \end{align} $$
$$ \begin{align} \partial_t \int_{\gamma_t} \kappa \,ds &= - \int_{\gamma_t} \kappa \tau^2 \, ds\nonumber \\\kern-20pt \partial_t \int_{\gamma_t} \kappa \log \kappa \,ds & = \int_{\gamma_t} (\log \kappa+1) (\partial_s^2 \kappa +\kappa^3-\kappa \tau^2) - \kappa^3 \log \kappa\, ds\nonumber \\\kern-20pt & = \int_{\gamma_t} -\frac{(\partial_s \kappa)^2}{\kappa} - (\kappa \log \kappa) \tau^2 + \kappa^3 - \kappa \tau^2 \, ds \end{align} $$
 $$ \begin{align} \partial_t \int_{\gamma_t} \kappa \log \tau \,ds & = \int_{\gamma_t} ( \partial_s^2 \kappa + \kappa^3 - \kappa \tau^2 )\log \tau\nonumber \\&\quad + \frac{\kappa}{\tau}( 2 \kappa^2 \tau + \partial_s (2 \tau \partial_s \log \kappa) +\partial_s^2 \tau ) - \kappa^3 \log \tau \,ds \nonumber \\& = \int_{\gamma_t} - \kappa \tau^2 \log \tau + 2 \kappa^3 - 2\frac{(\partial_s \kappa)^2}{\kappa} + \kappa (\partial_s \log \tau)^2 \, ds. \end{align} $$
$$ \begin{align} \partial_t \int_{\gamma_t} \kappa \log \tau \,ds & = \int_{\gamma_t} ( \partial_s^2 \kappa + \kappa^3 - \kappa \tau^2 )\log \tau\nonumber \\&\quad + \frac{\kappa}{\tau}( 2 \kappa^2 \tau + \partial_s (2 \tau \partial_s \log \kappa) +\partial_s^2 \tau ) - \kappa^3 \log \tau \,ds \nonumber \\& = \int_{\gamma_t} - \kappa \tau^2 \log \tau + 2 \kappa^3 - 2\frac{(\partial_s \kappa)^2}{\kappa} + \kappa (\partial_s \log \tau)^2 \, ds. \end{align} $$
Combining (3.2) and (3.3), we find the following evolution equation for the curvature-torsion entropy:
 $$ \begin{align} ~ \partial_t \int_{\gamma_t} \kappa \log\bigg( \frac{\tau}{\kappa^2} \bigg) \, ds = \int_{\gamma_t} -\kappa \tau^2 \log\bigg( \frac{\tau}{\kappa^2} \bigg) + \kappa (\partial_s \log \tau)^2+ 2 \kappa \tau^2 \, ds. \end{align} $$
$$ \begin{align} ~ \partial_t \int_{\gamma_t} \kappa \log\bigg( \frac{\tau}{\kappa^2} \bigg) \, ds = \int_{\gamma_t} -\kappa \tau^2 \log\bigg( \frac{\tau}{\kappa^2} \bigg) + \kappa (\partial_s \log \tau)^2+ 2 \kappa \tau^2 \, ds. \end{align} $$
This immediately provides a second proof that twisted curves cannot develop Type-I singularities. In particular, for a Type-I singularity,
![]() ${\tau }/{\kappa ^2}$
goes to zero uniformly (by Altschuler’s planarity theorem and the fact that all sequences to the singular time are essential). As such, the curvature-torsion entropy must go to negative infinity for a Type-I singularity. However, once
${\tau }/{\kappa ^2}$
goes to zero uniformly (by Altschuler’s planarity theorem and the fact that all sequences to the singular time are essential). As such, the curvature-torsion entropy must go to negative infinity for a Type-I singularity. However, once
![]() $\sup \log ({\tau }/{\kappa ^2})<2$
, the curvature-torsion entropy is increasing.
$\sup \log ({\tau }/{\kappa ^2})<2$
, the curvature-torsion entropy is increasing.
Furthermore, we can also show that
![]() $\log ({\tau }/{\kappa ^2})$
blows up along some sequence. Suppose that there is a uniform bound
$\log ({\tau }/{\kappa ^2})$
blows up along some sequence. Suppose that there is a uniform bound
Then (2.1) must go to negative infinity as t goes to
![]() $\omega $
. To see this, consider the region
$\omega $
. To see this, consider the region
![]() $S \subset \gamma _t$
where
$S \subset \gamma _t$
where
![]() $\log ({\tau }/{\kappa ^2})>0$
. On this set,
$\log ({\tau }/{\kappa ^2})>0$
. On this set,
 $$ \begin{align*}\int_S \kappa \log\bigg(\frac{\tau}{\kappa^2}\bigg) \,ds \leq C_1 \int_S \kappa \, ds \leq C_1 \int_{\gamma_0} \kappa \, ds, \end{align*} $$
$$ \begin{align*}\int_S \kappa \log\bigg(\frac{\tau}{\kappa^2}\bigg) \,ds \leq C_1 \int_S \kappa \, ds \leq C_1 \int_{\gamma_0} \kappa \, ds, \end{align*} $$
(since the total curvature is decreasing). As such, the positive part of the integral is bounded from above. However,
![]() $\gamma _t$
has a region that converges to a Grim Reaper curve, whose curvature-torsion entropy is
$\gamma _t$
has a region that converges to a Grim Reaper curve, whose curvature-torsion entropy is
![]() $-\infty $
.
$-\infty $
.
To reach a contradiction, we can estimate the left-hand side of (3.4) by
 $$ \begin{align*} \partial_t \int_{\gamma_t} \kappa \log\bigg( \frac{\tau}{\kappa^2} \bigg) \, ds \geq \int_{\gamma_t} - (C_1-2) \kappa \tau^2 \,ds = (C_1-2) \partial_t \int_{\gamma_t} \kappa \,ds. \end{align*} $$
$$ \begin{align*} \partial_t \int_{\gamma_t} \kappa \log\bigg( \frac{\tau}{\kappa^2} \bigg) \, ds \geq \int_{\gamma_t} - (C_1-2) \kappa \tau^2 \,ds = (C_1-2) \partial_t \int_{\gamma_t} \kappa \,ds. \end{align*} $$
Since the total curvature decreases to a positive limit as t goes to
![]() $\omega $
, this shows that the difference between the curvature-torsion entropy at the present time and the singular time is bounded from below, and so cannot go to negative infinity.
$\omega $
, this shows that the difference between the curvature-torsion entropy at the present time and the singular time is bounded from below, and so cannot go to negative infinity.
3.2 Points with large torsion and curvature
Theorem 2.1 shows that the potential singularities of a twisted curve are highly unusual and we suspect they cannot occur. One strategy would be to try to find an essential sequence so that
![]() $ {\tau }/{\kappa }$
does not go to zero. Although we cannot show this (or even that
$ {\tau }/{\kappa }$
does not go to zero. Although we cannot show this (or even that
![]() $\log ( {\tau }/{\kappa ^2} )$
goes to infinity along a blow-up sequence), we can show a weaker result in this direction.
$\log ( {\tau }/{\kappa ^2} )$
goes to infinity along a blow-up sequence), we can show a weaker result in this direction.
Proposition 3.3. Suppose
![]() $\gamma $
is a curve in
$\gamma $
is a curve in
![]() $\mathbb {R}^3$
which develops a twisted singularity. Then one of the following two possibilities occurs.
$\mathbb {R}^3$
which develops a twisted singularity. Then one of the following two possibilities occurs.
-
(1) There exists a sequence
 $(p_n,t_n)$
so that
$(p_n,t_n)$
so that
 $\kappa (p_n,t_n)\to 0$
.
$\kappa (p_n,t_n)\to 0$
. -
(2) There is a sequence
 $(p_n,t_n)$
so that both tend to infinity for
$(p_n,t_n)$
so that both tend to infinity for $$ \begin{align*}\tau \quad\textrm{and}\quad (2\kappa^2+2\partial_s^2 \log \kappa) (\omega-t_n)^\alpha\end{align*} $$
$$ \begin{align*}\tau \quad\textrm{and}\quad (2\kappa^2+2\partial_s^2 \log \kappa) (\omega-t_n)^\alpha\end{align*} $$
 $\alpha <1$
. Furthermore, this sequence consists of the points whose torsion is maximised on
$\alpha <1$
. Furthermore, this sequence consists of the points whose torsion is maximised on
 $\gamma _{t_n}$
.
$\gamma _{t_n}$
.
Proof. If we assume that
![]() $\kappa $
is bounded away from zero near the singular time, then Theorem 2.1 shows that
$\kappa $
is bounded away from zero near the singular time, then Theorem 2.1 shows that
![]() $\log ( \tau )$
must go to infinity, and thus we must show that we can extract a sequence so that
$\log ( \tau )$
must go to infinity, and thus we must show that we can extract a sequence so that
![]() $(2\kappa ^2+2\partial _s^2 \log \kappa )(\omega -t)^\alpha $
blows up. We calculate
$(2\kappa ^2+2\partial _s^2 \log \kappa )(\omega -t)^\alpha $
blows up. We calculate
 $$ \begin{align*} \partial_t \log (\tau) & = \frac{1}{\tau} \bigg(2\kappa^2\tau + \partial_s \bigg(\frac{2\tau}{\kappa} \partial_s \kappa \bigg) + \partial_s^2 \tau \bigg) \\ & = 2\kappa^2 +2 \partial_s^2 \log \kappa +2(\partial_s \log \tau )(\partial_s \log \kappa) + \frac{ \partial_s^2 \tau}{\tau}. \end{align*} $$
$$ \begin{align*} \partial_t \log (\tau) & = \frac{1}{\tau} \bigg(2\kappa^2\tau + \partial_s \bigg(\frac{2\tau}{\kappa} \partial_s \kappa \bigg) + \partial_s^2 \tau \bigg) \\ & = 2\kappa^2 +2 \partial_s^2 \log \kappa +2(\partial_s \log \tau )(\partial_s \log \kappa) + \frac{ \partial_s^2 \tau}{\tau}. \end{align*} $$
At the maximum of
![]() $\log ( \tau )$
, the maximum principle implies that
$\log ( \tau )$
, the maximum principle implies that
 $$ \begin{align*} \partial_s \log \tau = 0 \quad \textrm{and} \quad \frac{\partial_s^2 \tau}{\tau} \leq 0. \end{align*} $$
$$ \begin{align*} \partial_s \log \tau = 0 \quad \textrm{and} \quad \frac{\partial_s^2 \tau}{\tau} \leq 0. \end{align*} $$
At the maximum of
![]() $\log (\tau )$
, we find that
$\log (\tau )$
, we find that
However, for
![]() $\sup \log (\tau )$
to go to infinity in finite time, Hamilton’s maximum principle shows we must be able to extract a subsequence where
$\sup \log (\tau )$
to go to infinity in finite time, Hamilton’s maximum principle shows we must be able to extract a subsequence where
goes to infinity.
To show the stronger estimate
![]() $(2\kappa ^2+2\partial _s^2 \log \kappa (p_n,t_n))(\omega -t)^\alpha \to \infty $
, we suppose that this is not the case. Then, we divide up the time interval
$(2\kappa ^2+2\partial _s^2 \log \kappa (p_n,t_n))(\omega -t)^\alpha \to \infty $
, we suppose that this is not the case. Then, we divide up the time interval
![]() $(t,\omega )$
into sub-intervals
$(t,\omega )$
into sub-intervals
![]() $(t_i, {(\omega +t_i)}/{2})$
and apply the maximum principle on each sub-interval. Doing so, we obtain the estimate
$(t_i, {(\omega +t_i)}/{2})$
and apply the maximum principle on each sub-interval. Doing so, we obtain the estimate
 $$ \begin{align*} \sup_{t\leq t_n} \log \tau(p,t) -\sup \log \tau (p,t_0) \leq \sum_{i=0}^{n} \frac{C_2}{2^{i(1-\alpha)}}. \end{align*} $$
$$ \begin{align*} \sup_{t\leq t_n} \log \tau(p,t) -\sup \log \tau (p,t_0) \leq \sum_{i=0}^{n} \frac{C_2}{2^{i(1-\alpha)}}. \end{align*} $$
This estimate is uniformly bounded in n, giving a contradiction.
A similar argument shows that we can extract sequences so that both
![]() $\kappa ^\rho \tau $
and
$\kappa ^\rho \tau $
and
![]() $((2+\rho )\kappa ^2+2\partial _s^2 \log \kappa )(t-\omega )^\alpha $
go to infinity for any
$((2+\rho )\kappa ^2+2\partial _s^2 \log \kappa )(t-\omega )^\alpha $
go to infinity for any
![]() $\rho \in (0,1].$
However, we cannot conclude that
$\rho \in (0,1].$
However, we cannot conclude that
![]() $\tau $
must go to infinity on such a sequence, so we do not have a geometric application for this fact.
$\tau $
must go to infinity on such a sequence, so we do not have a geometric application for this fact.
3.3 A related quantity
As can be seen from Theorems 2.1 and 3.1, it is possible to control the behaviour of curve shortening flow by finding quantities that are monotone (or nearly monotone) under the flow. There are several other quantities whose evolution is quite simple, and it might be possible to use them to control the singularities that emerge under the flow. For instance, the quantity
![]() $\int _{\gamma _t} \tau \log ( {\tau ^2}/{\kappa ^4} ) \, ds$
evolves as follows:
$\int _{\gamma _t} \tau \log ( {\tau ^2}/{\kappa ^4} ) \, ds$
evolves as follows:
 $$ \begin{align*} \partial_t \int_{\gamma_t} \tau \log\bigg( \frac{\tau^2}{\kappa^4} \bigg) \, ds = \int_{\gamma_t} \bigg(\kappa^2 \tau \log\bigg( \frac{\tau^2}{\kappa^4} \bigg) + \tau \bigg((\partial_s \log \kappa^2)^2-\frac{1}{2}(\partial_s \log \tau^2)^2 \bigg) +4 \tau^3\bigg) \, ds. \end{align*} $$
$$ \begin{align*} \partial_t \int_{\gamma_t} \tau \log\bigg( \frac{\tau^2}{\kappa^4} \bigg) \, ds = \int_{\gamma_t} \bigg(\kappa^2 \tau \log\bigg( \frac{\tau^2}{\kappa^4} \bigg) + \tau \bigg((\partial_s \log \kappa^2)^2-\frac{1}{2}(\partial_s \log \tau^2)^2 \bigg) +4 \tau^3\bigg) \, ds. \end{align*} $$
In this expression, the terms in the argument of the logarithm have been squared so that this quantity is well defined for arbitrary space curves without assuming they are twisted. We do not know of a direct geometric application for this quantity. However, the fact that the evolution is so simple suggests that it may be useful for controlling the formation of singularities.
4 A heuristic for the emergence of flat points
It remains an open question to determine the limiting behaviour for generic initial data for spatial curve shortening flow. However, it is reasonable to expect that generic curves converge to round points, the same as for embedded curves in the plane. There are several cases where spatial curve shortening flow is known to converge to a round point. For instance, if the curve is embedded on a standard sphere, we have the following result (a proof can be found in [Reference Siming10]).
Theorem 4.1. Given a curve
![]() $\gamma _0$
embedded on a standard sphere
$\gamma _0$
embedded on a standard sphere
![]() $S^2$
in
$S^2$
in
![]() ${\mathbb {R}}^3$
, under curve shortening flow,
${\mathbb {R}}^3$
, under curve shortening flow,
![]() $\gamma _t$
remains embedded on a shrinking sphere and converges to a round point.
$\gamma _t$
remains embedded on a shrinking sphere and converges to a round point.
Note that the total torsion of a spherical curve is zero, which immediately implies that any such curve has flat points. In fact, Sedykh’s theorem shows there are at least four such points [Reference Sedykh9]. Furthermore, in recent work, Litzinger showed that curves whose entropy is at most
![]() $2$
converge to round points.
$2$
converge to round points.
Theorem 4.2 [Reference Litzinger8].
Suppose that
![]() ${\gamma }$
is a smooth curve whose entropy
${\gamma }$
is a smooth curve whose entropy
 $$ \begin{align*} \lambda({\gamma})=\sup _{x_0 \in \mathbb{R}^n,\, t_0>0}(4 \pi t_0)^{-{1}/{2}} \int_{\gamma_t} {e}^{-{|x-x_0|^2}/{4 t_0}} \,d \mu \end{align*} $$
$$ \begin{align*} \lambda({\gamma})=\sup _{x_0 \in \mathbb{R}^n,\, t_0>0}(4 \pi t_0)^{-{1}/{2}} \int_{\gamma_t} {e}^{-{|x-x_0|^2}/{4 t_0}} \,d \mu \end{align*} $$
satisfies
![]() $\lambda ({\gamma }) \leq 2$
. Then under curve shortening flow,
$\lambda ({\gamma }) \leq 2$
. Then under curve shortening flow,
![]() ${\gamma _t}$
converges to a round point.
${\gamma _t}$
converges to a round point.
Apart from these results, there is another reason why we do not expect initially twisted curves to remain twisted; the reaction terms for the curvature and torsion tend to create points of vanishing curvature. To see this, we ignore the spatial derivative terms in (3.1) describing the evolution of
![]() $\kappa $
and
$\kappa $
and
![]() $\tau $
and simply consider the system of coupled ordinary differential equations (ODEs)
$\tau $
and simply consider the system of coupled ordinary differential equations (ODEs)
This system reduces to the homogeneous equation
whose solutions are circular arcs of the form
As such, no matter how large
![]() $\kappa $
is initially, the reaction ODE tends towards a situation where
$\kappa $
is initially, the reaction ODE tends towards a situation where
![]() $\kappa $
vanishes. The full evolution equation for the torsion also includes a complicated term involving its derivatives and those of the curvature, so this analysis does not constitute a complete proof. However, if the initial curve is a helix (a curve of constant curvature and torsion), this calculation shows that the limiting configuration is a straight line, but the limiting value of the torsion is nonzero. The limiting value of the torsion is not the torsion of a straight line, which is undefined. Indeed, the limiting value depends on the initial curvature and torsion of the helix.
$\kappa $
vanishes. The full evolution equation for the torsion also includes a complicated term involving its derivatives and those of the curvature, so this analysis does not constitute a complete proof. However, if the initial curve is a helix (a curve of constant curvature and torsion), this calculation shows that the limiting configuration is a straight line, but the limiting value of the torsion is nonzero. The limiting value of the torsion is not the torsion of a straight line, which is undefined. Indeed, the limiting value depends on the initial curvature and torsion of the helix.
Acknowledgements
The author would like to thank Xuan Hien Nguyen, Mizan Khan and Kori Khan for their helpful comments.