Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gutman, Ivan
2016.
On Steiner degree distance of trees.
Applied Mathematics and Computation,
Vol. 283,
Issue. ,
p.
163.
Gutman, Ivan
Furtula, Boris
and
Das, Kinkar Ch.
2016.
On some degree-and-distance-based graph invariants of trees.
Applied Mathematics and Computation,
Vol. 289,
Issue. ,
p.
1.
Guo, Haili
2019.
The Vertex Degree Distance of One Vertex Union of Two Cycles.
Journal of Physics: Conference Series,
Vol. 1302,
Issue. 4,
p.
042041.
Mao, Yaping
Wang, Zhao
and
Das, Kinkar Ch.
2019.
Steiner Degree Distance of Two Graph Products.
Analele Universitatii "Ovidius" Constanta - Seria Matematica,
Vol. 27,
Issue. 2,
p.
83.
Zhang, Leilei
Li, Qishun
Li, Shuchao
and
Zhang, Minjie
2020.
The expected values for the Schultz index, Gutman index, multiplicative degree-Kirchhoff index and additive degree-Kirchhoff index of a random polyphenylene chain.
Discrete Applied Mathematics,
Vol. 282,
Issue. ,
p.
243.
Azari, Mahdieh
2020.
Further results on Zagreb eccentricity coindices.
Discrete Mathematics, Algorithms and Applications,
Vol. 12,
Issue. 06,
p.
2050075.
Li, Xueliang
Li, Yiyang
and
Wang, Zhiqian
2020.
The asymptotic value of energy for matrices with degree-distance-based entries of random graphs.
Linear Algebra and its Applications,
Vol. 603,
Issue. ,
p.
390.
Zhang, Jinlian
Peng, Xuhui
and
Chen, Hanlin
2021.
The limiting behaviours for the Gutman index, Schultz index, multiplicative degree-Kirchhoff index and additive degree-Kirchhoff index of a random polyphenylene chain.
Discrete Applied Mathematics,
Vol. 299,
Issue. ,
p.
62.
VETRÍK, Tomáš
2021.
General degree distance of graphs.
Journal of Algebra Combinatorics Discrete Structures and Applications,
Vol. 8,
Issue. 2,
p.
107.
Zhu, Wanlin
and
Geng, Xianya
2022.
Enumeration of the Multiplicative Degree-Kirchhoff Index in the Random Polygonal Chains.
Molecules,
Vol. 27,
Issue. 17,
p.
5669.
Geng, Xianya
and
Zhu, Wanlin
2022.
Enumeration of the Additive Degree–Kirchhoff Index in the Random Polygonal Chains.
Axioms,
Vol. 11,
Issue. 8,
p.
373.
Imran, Muhammad
Akhtar, Shehnaz
Ahmad, Uzma
Ahmad, Sarfraz
and
Bilal, Ahsan
2022.
On Extremal Graphs of Degree Distance Index by Using Edge-Grafting
Transformations Method.
Combinatorial Chemistry & High Throughput Screening,
Vol. 25,
Issue. 3,
p.
560.
Zhu, Wanlin
Fang, Minglei
and
Geng, Xianya
2022.
Enumeration of the Gutman and Schultz indices in the random polygonal chains.
Mathematical Biosciences and Engineering,
Vol. 19,
Issue. 11,
p.
10826.
Liu, Xinmei
and
Zhan, Qian
2022.
The Expected Values for the Gutman Index and Schultz Index in the Random Regular Polygonal Chains.
Molecules,
Vol. 27,
Issue. 20,
p.
6838.
Xie, Haiyan
Xue, Nini
and
Yang, Jingjing
2022.
The Vertex Degree Distances of One Vertex Union of the Cycle and the Star.
Journal of Physics: Conference Series,
Vol. 2173,
Issue. 1,
p.
012067.
Mafuta, P.
and
Mukwembi, S.
2023.
Average distance and connected domination.
AKCE International Journal of Graphs and Combinatorics,
Vol. 20,
Issue. 1,
p.
61.
Qi, Jinfeng
Fang, Minglei
and
Geng, Xianya
2023.
The Expected Value for the Wiener Index in the Random Spiro Chains.
Polycyclic Aromatic Compounds,
Vol. 43,
Issue. 2,
p.
1788.
Liu, Jia‐Bao
Gu, Jiao‐Jiao
and
Wang, Kang
2023.
The expected values for the Gutman index, Schultz index, and some Sombor indices of a random cyclooctane chain.
International Journal of Quantum Chemistry,
Vol. 123,
Issue. 3,
Liu, Hongfang
Liang, Jinxia
Liu, Yuhu
and
Das, Kinkar Chandra
2023.
A Combinatorial Approach to Study the Nordhaus–Guddum-Type Results for Steiner Degree Distance.
Mathematics,
Vol. 11,
Issue. 3,
p.
738.
Tao, Chen
Tang, Shengjun
and
Geng, Xianya
2023.
Statistical Analyses of a Class of Random Cyclooctatetraene Chain Networks with Respect to Several Topological Properties.
Symmetry,
Vol. 15,
Issue. 11,
p.
1971.
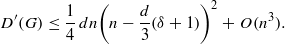 \[ D^\prime (G)\le \frac {1}{4}\,dn\biggl (n-\frac {d}{3}(\delta +1)\biggr )^2+O(n^3). \]
\[ D^\prime (G)\le \frac {1}{4}\,dn\biggl (n-\frac {d}{3}(\delta +1)\biggr )^2+O(n^3). \]