Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
XIONG, RAN
and
TANG, MIN
2014.
UNIQUE REPRESENTATION BI-BASIS FOR THE INTEGERS.
Bulletin of the Australian Mathematical Society,
Vol. 89,
Issue. 3,
p.
460.
TANG, MIN
2016.
A UNIQUE REPRESENTATION BI-BASIS FOR THE INTEGERS. II.
Bulletin of the Australian Mathematical Society,
Vol. 94,
Issue. 1,
p.
1.
Helou, Charles
2017.
Combinatorial and Additive Number Theory II.
Vol. 220,
Issue. ,
p.
139.


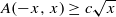 for infinitely many positive integers
for infinitely many positive integers 