No CrossRef data available.
Article contents
THE DIAMETER AND RADIUS OF RADIALLY MAXIMAL GRAPHS
Published online by Cambridge University Press: 11 January 2021
Abstract
A graph is called radially maximal if it is not complete and the addition of any new edge decreases its radius. Harary and Thomassen [‘Anticritical graphs’, Math. Proc. Cambridge Philos. Soc. 79(1) (1976), 11–18] proved that the radius r and diameter d of any radially maximal graph satisfy 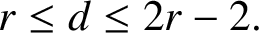 $r\le d\le 2r-2.$ Dutton et al. [‘Changing and unchanging of the radius of a graph’, Linear Algebra Appl. 217 (1995), 67–82] rediscovered this result with a different proof and conjectured that the converse is true, that is, if r and d are positive integers satisfying
$r\le d\le 2r-2.$ Dutton et al. [‘Changing and unchanging of the radius of a graph’, Linear Algebra Appl. 217 (1995), 67–82] rediscovered this result with a different proof and conjectured that the converse is true, that is, if r and d are positive integers satisfying 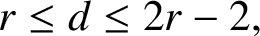 $r\le d\le 2r-2,$ then there exists a radially maximal graph with radius r and diameter
$r\le d\le 2r-2,$ then there exists a radially maximal graph with radius r and diameter 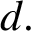 $d.$ We prove this conjecture and a little more.
$d.$ We prove this conjecture and a little more.
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 104 , Issue 2 , October 2021 , pp. 196 - 202
- Copyright
- © 2021 Australian Mathematical Publishing Association Inc.
Footnotes
This research was supported by the NSFC grants 11671148 and 11771148 and the Science and Technology Commission of Shanghai Municipality (STCSM) grant 18dz2271000.


