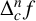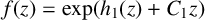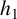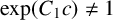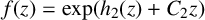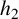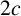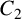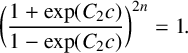1 Introduction
Let f be a meromorphic function on the complex plane
![]() ${\mathbb C}$
. We assume that the reader is familiar with the fundamental results and the standard notation of the Nevanlinna value distribution theory. We refer readers to [Reference Hayman12, Reference Yang and Yi16, Reference Yang17] for more details. A quick introduction of some basic notions in Nevanlinna theory can be found in Section 2.
${\mathbb C}$
. We assume that the reader is familiar with the fundamental results and the standard notation of the Nevanlinna value distribution theory. We refer readers to [Reference Hayman12, Reference Yang and Yi16, Reference Yang17] for more details. A quick introduction of some basic notions in Nevanlinna theory can be found in Section 2.
For any
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $c\in \mathbb {C}\backslash \{0\}$
, we define the forward difference operator
$c\in \mathbb {C}\backslash \{0\}$
, we define the forward difference operator
![]() $\Delta _c f(z)$
by
$\Delta _c f(z)$
by
and, by induction,
In addition, we use the usual notation
![]() $\Delta f(z)$
for
$\Delta f(z)$
for
![]() $c=1$
.
$c=1$
.
In 1935, Csillag [Reference Csillag6] proved the following result.
Theorem 1.1. Let
![]() $m, \,n$
be two distinct positive integers and let f be a transcendental entire function. If
$m, \,n$
be two distinct positive integers and let f be a transcendental entire function. If
![]() $f\not =0$
,
$f\not =0$
,
![]() $f^{(m)}\not =0$
,
$f^{(m)}\not =0$
,
![]() $f^{(n)}\not =0$
, then
$f^{(n)}\not =0$
, then
![]() $f(z)=e^{az+b}$
, where
$f(z)=e^{az+b}$
, where
![]() $a\,(\not = 0), b$
are constants.
$a\,(\not = 0), b$
are constants.
Tumura [Reference Tumura15], Hayman [Reference Hayman11] and Clunie [Reference Clunie5] improved Theorem 1.1 as follows.
Theorem 1.2. Let
![]() $n\,(\ge 2)$
be a positive integer and let f be a transcendental entire function. If
$n\,(\ge 2)$
be a positive integer and let f be a transcendental entire function. If
![]() $f\not =0$
,
$f\not =0$
,
![]() $f^{(n)}\not =0$
, then
$f^{(n)}\not =0$
, then
![]() $f(z)=e^{az+b}$
, where
$f(z)=e^{az+b}$
, where
![]() $a\,(\not = 0), b$
are constants.
$a\,(\not = 0), b$
are constants.
Recently, there has been growing interest in difference analogues of the value distribution of meromorphic functions (see [Reference Chen and Shon2–Reference Chiang and Feng4, Reference Halburd and Korhonen8–Reference Halburd, Korhonen and Tohge10]). In 2013, Chen [Reference Chen1] obtained a difference analogue of Theorems 1.1 and 1.2.
Theorem 1.3. Let f be a transcendental entire function of finite order, let c be a nonzero constant and let n be a positive integer. If
![]() $f\not = 0$
,
$f\not = 0$
,
![]() $\Delta _c^n f\not = 0$
, then
$\Delta _c^n f\not = 0$
, then
![]() $f(z)=e^{az+b}$
, where
$f(z)=e^{az+b}$
, where
![]() $a\,(\not = 0), b$
are constants.
$a\,(\not = 0), b$
are constants.
The conclusion in Theorem 1.3 does not hold without a growth condition on f. For example, if
![]() $f(z)=\exp (\sin (2\pi z)+z)$
, then
$f(z)=\exp (\sin (2\pi z)+z)$
, then
![]() $\Delta ^n f\not =0$
for any
$\Delta ^n f\not =0$
for any
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
Inspired by Theorems 1.2 and 1.3, together with the above example, we naturally pose the following question.
Question 1.4. What can we say if f is a transcendental entire function in Theorem 1.3 without a further assumption on the growth order?
We consider this question and obtain the following result.
Theorem 1.5. Let f be a transcendental entire function, let c be a nonzero constant and let n be a positive integer. If
![]() $f\not = 0$
,
$f\not = 0$
,
![]() $\Delta _c^n f\not = 0$
, then either
$\Delta _c^n f\not = 0$
, then either
where
![]() $h_1$
is an entire function of period c and
$h_1$
is an entire function of period c and
![]() $\exp (C_1 c)\neq 1$
, or
$\exp (C_1 c)\neq 1$
, or
where
![]() $h_2$
is an entire function of period
$h_2$
is an entire function of period
![]() $2c$
and
$2c$
and
![]() $C_2$
satisfies
$C_2$
satisfies
 $$ \begin{align*} \bigg(\frac{1+\exp(C_2c)}{1-\exp(C_2 c)}\bigg)^{2n}=1. \end{align*} $$
$$ \begin{align*} \bigg(\frac{1+\exp(C_2c)}{1-\exp(C_2 c)}\bigg)^{2n}=1. \end{align*} $$
As an application of Theorem 1.5, we obtain the following result which improves Theorem 1.3.
Theorem 1.6. Let f be a transcendental entire function of hyper-order less than
![]() $1$
and c be a nonzero constant. Assume that f and
$1$
and c be a nonzero constant. Assume that f and
![]() $\Delta _{c}^n f$
omit zero in the whole complex plane for some
$\Delta _{c}^n f$
omit zero in the whole complex plane for some
![]() $n\in \mathbb {N}$
. Then
$n\in \mathbb {N}$
. Then
![]() $f(z)=e^{az+b}$
, where
$f(z)=e^{az+b}$
, where
![]() $a\neq 0$
and b are constants.
$a\neq 0$
and b are constants.
Frank [Reference Frank7] and Langley [Reference Langley13] proved that Theorem 1.2 remains valid for meromorphic functions. They obtained the following theorem.
Theorem 1.7. Let
![]() $n\,(\ge 2)$
be a positive integer and let f be a transcendental meromorphic function. If
$n\,(\ge 2)$
be a positive integer and let f be a transcendental meromorphic function. If
![]() $f\not =0$
,
$f\not =0$
,
![]() $f^{(n)}\not =0$
, then
$f^{(n)}\not =0$
, then
![]() $f(z)=e^{az+b}$
, where
$f(z)=e^{az+b}$
, where
![]() $a\,(\not = 0), b$
are constants.
$a\,(\not = 0), b$
are constants.
Based on Theorems 1.2, 1.3 and 1.7, it is natural to ask whether Theorem 1.3 is valid or not for meromorphic functions. The following example shows that the answer to this question is in the negative.
Example 1.8. Let b and c be two complex numbers in
![]() $\mathbb {C}\backslash \{0\}$
. For any entire function
$\mathbb {C}\backslash \{0\}$
. For any entire function
![]() $H(z)$
with period c and
$H(z)$
with period c and
![]() $n\in \mathbb {N}$
, we can always construct a polynomial
$n\in \mathbb {N}$
, we can always construct a polynomial
![]() $P(z)$
of degree n such that
$P(z)$
of degree n such that
![]() $\Delta _c^nP(z)\equiv b$
and each zero of
$\Delta _c^nP(z)\equiv b$
and each zero of
![]() $P(z)$
is also a zero of
$P(z)$
is also a zero of
![]() $1-e^{H(z)}$
. Let
$1-e^{H(z)}$
. Let
![]() ${f(z)={P(z)}/{1-e^{H(z)}}}$
. Then both
${f(z)={P(z)}/{1-e^{H(z)}}}$
. Then both
![]() $f(z)$
and
$f(z)$
and
![]() $\Delta _c^nf(z)$
omit zero.
$\Delta _c^nf(z)$
omit zero.
2 Preliminaries
In this section, we collect some basic results which will be used in the proof of our main results.
Let us recall some basic notation of Nevanlinna theory. Let f be a nonconstant meromorphic function. The Nevanlinna characteristic is defined by
where
![]() $m(r,f)$
is the proximity function defined by
$m(r,f)$
is the proximity function defined by
 $$ \begin{align*} m(r,f)=\frac{1}{2\pi}\int_{0}^{2\pi}\log^{+}|f(re^{i\theta})|\,d\theta \end{align*} $$
$$ \begin{align*} m(r,f)=\frac{1}{2\pi}\int_{0}^{2\pi}\log^{+}|f(re^{i\theta})|\,d\theta \end{align*} $$
and
![]() $N(r,f)$
denotes the integrated counting function of poles of f defined by
$N(r,f)$
denotes the integrated counting function of poles of f defined by
 $$ \begin{align*} N(r, f)=\int_{0}^{r}\frac{n(t, f)-n(0,f)}{t}\,dt+n(0,f)\log r \end{align*} $$
$$ \begin{align*} N(r, f)=\int_{0}^{r}\frac{n(t, f)-n(0,f)}{t}\,dt+n(0,f)\log r \end{align*} $$
and
![]() $n(t,f)$
is the number of poles of f in
$n(t,f)$
is the number of poles of f in
![]() $\{z: |z|\le t\}$
counting multiplicities. The order and the hyper-order of f are defined by
$\{z: |z|\le t\}$
counting multiplicities. The order and the hyper-order of f are defined by
 $$ \begin{align*}\ \rho(f)=\limsup_{r\rightarrow\infty}\frac{\log^{+}T(r,f)}{\log r}\end{align*} $$
$$ \begin{align*}\ \rho(f)=\limsup_{r\rightarrow\infty}\frac{\log^{+}T(r,f)}{\log r}\end{align*} $$
and
 $$ \begin{align*}\rho_{2}(f)=\limsup_{r\rightarrow\infty}\frac{\log ^{+}\log ^{+}T(r,f)}{\log r}.\end{align*} $$
$$ \begin{align*}\rho_{2}(f)=\limsup_{r\rightarrow\infty}\frac{\log ^{+}\log ^{+}T(r,f)}{\log r}.\end{align*} $$
In addition, for any entire function f and
![]() $r>0$
, the maximum modulus of f is denoted by
$r>0$
, the maximum modulus of f is denoted by
The order and the hyper-order of an entire function f can also be defined by
 $$ \begin{align*}\ \rho(f)=\limsup_{r\rightarrow\infty}\frac{\log^{+}\log^{+}M(r,f)}{\log r}\end{align*} $$
$$ \begin{align*}\ \rho(f)=\limsup_{r\rightarrow\infty}\frac{\log^{+}\log^{+}M(r,f)}{\log r}\end{align*} $$
and
 $$ \begin{align*}\rho_{2}(f)=\limsup_{r\rightarrow\infty}\frac{\log ^{+}\log ^{+}\log^{+}M(r,f)}{\log r}.\end{align*} $$
$$ \begin{align*}\rho_{2}(f)=\limsup_{r\rightarrow\infty}\frac{\log ^{+}\log ^{+}\log^{+}M(r,f)}{\log r}.\end{align*} $$
To prove our results, we need Pólya’s lemma on the growth of the composite of two entire functions.
Lemma 2.1 (Pólya’s lemma, [Reference Pólya14]).
Let f and g be two entire functions. Then
for some constant
![]() $C>0$
, where
$C>0$
, where
![]() $(f\circ g)(z)=f(g(z))$
for any
$(f\circ g)(z)=f(g(z))$
for any
![]() $z\in \mathbb {C}$
.
$z\in \mathbb {C}$
.
We also need the following version of Borel’s theorem.
Lemma 2.2 (Borel’s theorem, [Reference Yang and Yi16]).
Let
![]() $p_{j}, \ q_j \ (j=1, \ldots , n)$
be entire functions such that:
$p_{j}, \ q_j \ (j=1, \ldots , n)$
be entire functions such that:
-
(i)
 $\sum _{j=1}^{n}p_{j} e^{q_{j}}\equiv 0$
;
$\sum _{j=1}^{n}p_{j} e^{q_{j}}\equiv 0$
; -
(ii)
 $q_{s}-q_{t}$
is not constant for
$q_{s}-q_{t}$
is not constant for
 $1\leq s<t\leq n$
;
$1\leq s<t\leq n$
; -
(iii)
 $T(r,p_j)=o\{T(r,e^{q_s-q_t})\} \ (r\to \infty , r\not \in E)$
for
$T(r,p_j)=o\{T(r,e^{q_s-q_t})\} \ (r\to \infty , r\not \in E)$
for
 $1\leq j\leq n$
,
$1\leq j\leq n$
,
 $1\leq s<t\leq n$
, where E is of finite linear measure or finite logarithmic measure.
$1\leq s<t\leq n$
, where E is of finite linear measure or finite logarithmic measure.
Then
![]() $p_{j}\equiv 0$
for
$p_{j}\equiv 0$
for
![]() $j=1, \ldots , n$
.
$j=1, \ldots , n$
.
By Lemma 2.2, we can immediately obtain the following lemma, which is crucial in the proof of our main result.
Lemma 2.3. Let
![]() $f_0, \ldots , f_{m-1}$
be nonconstant entire functions such that
$f_0, \ldots , f_{m-1}$
be nonconstant entire functions such that
![]() $f_{s}-f_{t}$
is not constant for
$f_{s}-f_{t}$
is not constant for
![]() $0\leq s<t\leq m-1$
and let
$0\leq s<t\leq m-1$
and let
![]() $a_0, \ldots , a_m$
be nonzero entire functions such that
$a_0, \ldots , a_m$
be nonzero entire functions such that
![]() $T(r,a_j)=o\{T(r,e^{f_s-f_t})\}$
$T(r,a_j)=o\{T(r,e^{f_s-f_t})\}$
![]() $(r\to \infty , r\not \in E)$
for
$(r\to \infty , r\not \in E)$
for
![]() $0\leq j \leq m$
,
$0\leq j \leq m$
,
![]() $0\leq s<t\leq m-1$
, where E is of finite logarithmic measure. If there exists an entire function g such that
$0\leq s<t\leq m-1$
, where E is of finite logarithmic measure. If there exists an entire function g such that
then
![]() $m=1$
.
$m=1$
.
Proof. If
![]() $m=1$
, we are done. Assume that
$m=1$
, we are done. Assume that
![]() $m\geq 2$
. From Lemma 2.2, there exists i with
$m\geq 2$
. From Lemma 2.2, there exists i with
![]() $0\leq i\leq m-1$
such that
$0\leq i\leq m-1$
such that
![]() $g(z)-f_{i}(z)\equiv C_1$
for some constant
$g(z)-f_{i}(z)\equiv C_1$
for some constant
![]() $C_1$
. Thus,
$C_1$
. Thus,
 $$ \begin{align*} (a_i-a_m e^{C_1})e^{f_i}+\sum_{j=0, j\neq i}^{m-1} a_j e^{f_{j}}\equiv 0. \end{align*} $$
$$ \begin{align*} (a_i-a_m e^{C_1})e^{f_i}+\sum_{j=0, j\neq i}^{m-1} a_j e^{f_{j}}\equiv 0. \end{align*} $$
Therefore, by Lemma 2.2, we deduce
![]() $a_j=0, j\neq i$
, which leads to a contradiction. Thus, the integer
$a_j=0, j\neq i$
, which leads to a contradiction. Thus, the integer
![]() $m=1$
.
$m=1$
.
3 Proof of Theorem 1.5
Proof. By rescaling
![]() $f(z)$
using the transformation
$f(z)$
using the transformation
![]() $g(z) = f(cz)$
, we may assume without loss of generality that
$g(z) = f(cz)$
, we may assume without loss of generality that
![]() $c=1$
. Since f and
$c=1$
. Since f and
![]() $\Delta ^n f$
omit zero in
$\Delta ^n f$
omit zero in
![]() $\mathbb {C}$
for some
$\mathbb {C}$
for some
![]() $n\in \mathbb {N}$
, there exist two entire functions g and h such that
$n\in \mathbb {N}$
, there exist two entire functions g and h such that
It follows that
 $$ \begin{align} (-1)^n\sum_{k=0}^{n}C_{n}^{k}(-1)^k e^{g(z+k)}=e^{h(z)}. \end{align} $$
$$ \begin{align} (-1)^n\sum_{k=0}^{n}C_{n}^{k}(-1)^k e^{g(z+k)}=e^{h(z)}. \end{align} $$
We divide our proof into three steps.
Step 1. We claim that there exists a constant D and a positive integer l
![]() $(1\le l \le n)$
such that
$(1\le l \le n)$
such that
Indeed, if there is no such l, then for
![]() $0\leq i<j\leq n$
,
$0\leq i<j\leq n$
,
(because otherwise,
![]() $g(z+j-i)-g(z)\equiv \mbox {constant}$
and we can choose
$g(z+j-i)-g(z)\equiv \mbox {constant}$
and we can choose
![]() $l=j-i$
, which contradicts our assumption). Applying Lemma 2.3 to (3.1) yields
$l=j-i$
, which contradicts our assumption). Applying Lemma 2.3 to (3.1) yields
![]() $n=0$
, which is impossible. This verifies our claim.
$n=0$
, which is impossible. This verifies our claim.
Step 2. We claim that either
![]() $l=1$
or
$l=1$
or
![]() $l=2$
. Suppose the conclusion is not true, that is,
$l=2$
. Suppose the conclusion is not true, that is,
![]() $l\ge 3$
. It is easy to see that
$l\ge 3$
. It is easy to see that
 $$ \begin{align} (-1)^n e^{h(z)}=&\sum_{k=0}^{n}C_{n}^{k}(-1)^k e^{g(z+k)} \nonumber\\ =&\sum_{j=0}^{l-1}\sum_{k\equiv j \pmod l,\, k\leq n}C_{n}^{k}(-1)^k e^{g(z+k)} \nonumber\\ =&\sum_{j=0}^{l-1}\sum_{k\equiv j \pmod l,\, k\leq n}C_{n}^{k}(-1)^k e^{{(k-j)D}/{l}} e^{g(z+j)} \nonumber\\ =&\sum_{j=0}^{l-1}e^{g(z+j)} \sum_{k\equiv j \pmod l,\, k\leq n}C_{n}^{k}(-1)^k e^{{(k-j)D}/{l}}. \end{align} $$
$$ \begin{align} (-1)^n e^{h(z)}=&\sum_{k=0}^{n}C_{n}^{k}(-1)^k e^{g(z+k)} \nonumber\\ =&\sum_{j=0}^{l-1}\sum_{k\equiv j \pmod l,\, k\leq n}C_{n}^{k}(-1)^k e^{g(z+k)} \nonumber\\ =&\sum_{j=0}^{l-1}\sum_{k\equiv j \pmod l,\, k\leq n}C_{n}^{k}(-1)^k e^{{(k-j)D}/{l}} e^{g(z+j)} \nonumber\\ =&\sum_{j=0}^{l-1}e^{g(z+j)} \sum_{k\equiv j \pmod l,\, k\leq n}C_{n}^{k}(-1)^k e^{{(k-j)D}/{l}}. \end{align} $$
For simplification, write
![]() $E=e^{{D}/{l}}$
and
$E=e^{{D}/{l}}$
and
 $$ \begin{align*} \phi_{j}(E):=\sum_{k\equiv j \pmod l,\, k\leq n}C_{n}^{k}(-1)^k E^{k-j}. \end{align*} $$
$$ \begin{align*} \phi_{j}(E):=\sum_{k\equiv j \pmod l,\, k\leq n}C_{n}^{k}(-1)^k E^{k-j}. \end{align*} $$
For any
![]() $E\in \mathbb {C}\backslash \{0\}$
, we define
$E\in \mathbb {C}\backslash \{0\}$
, we define
We claim that
![]() $\sharp \mathcal {L}_{E}=1$
. Indeed, by (3.1),
$\sharp \mathcal {L}_{E}=1$
. Indeed, by (3.1),
![]() $\sharp \mathcal {L}_{E}\ge 1$
. If
$\sharp \mathcal {L}_{E}\ge 1$
. If
![]() $\sharp \mathcal {L}_{E}\ge 2$
, then we can rewrite (3.2) as
$\sharp \mathcal {L}_{E}\ge 2$
, then we can rewrite (3.2) as
 $$ \begin{align*} \sum_{j\in \mathcal{L}_{E}} \phi_j(E) e^{g(z+j)}=(-1)^n e^{h(z)}, \end{align*} $$
$$ \begin{align*} \sum_{j\in \mathcal{L}_{E}} \phi_j(E) e^{g(z+j)}=(-1)^n e^{h(z)}, \end{align*} $$
in contradiction to Lemma 2.3. Therefore,
![]() $\sharp \mathcal {L}_{E}=1$
. It follows that there exists an integer p
$\sharp \mathcal {L}_{E}=1$
. It follows that there exists an integer p
![]() $(0\leq p\leq l-1)$
such that
$(0\leq p\leq l-1)$
such that
with
![]() $j\neq p$
,
$j\neq p$
,
![]() $0\le j \le l-1$
. Let
$0\le j \le l-1$
. Let
![]() $\omega _{l}=e^{{2\pi i}/{l}}$
. Note that for any fixed j, we have
$\omega _{l}=e^{{2\pi i}/{l}}$
. Note that for any fixed j, we have
![]() $\omega _{l}^{k-j}=1$
if
$\omega _{l}^{k-j}=1$
if
![]() $k\equiv j \pmod l$
. Therefore,
$k\equiv j \pmod l$
. Therefore,
 $$ \begin{align} \phi_{j}(E)&=\sum_{k\equiv j \pmod l,\, k\leq n}C_{n}^{k}(-1)^k E^{k-j}\nonumber\\ &=\frac{1}{l}\sum_{k=0}^{n}C_{n}^k(-1)^kE^{k-j}\sum_{t=0}^{l-1}(\omega_l^t)^{k-j}\nonumber\\ &=\frac1{l}\sum_{t=0}^{l-1}\sum_{k=0}^{n}C_{n}^k(-1)^k(\omega_l^t E)^{k-j}\nonumber\\ &=\frac{1}{l}\sum_{t=0}^{l-1}\frac{(1-\omega_{l}^{t}E)^{n}}{\omega_{l}^{tj}E^j}. \end{align} $$
$$ \begin{align} \phi_{j}(E)&=\sum_{k\equiv j \pmod l,\, k\leq n}C_{n}^{k}(-1)^k E^{k-j}\nonumber\\ &=\frac{1}{l}\sum_{k=0}^{n}C_{n}^k(-1)^kE^{k-j}\sum_{t=0}^{l-1}(\omega_l^t)^{k-j}\nonumber\\ &=\frac1{l}\sum_{t=0}^{l-1}\sum_{k=0}^{n}C_{n}^k(-1)^k(\omega_l^t E)^{k-j}\nonumber\\ &=\frac{1}{l}\sum_{t=0}^{l-1}\frac{(1-\omega_{l}^{t}E)^{n}}{\omega_{l}^{tj}E^j}. \end{align} $$
Thus, we can write (3.3) in the form
 $$ \begin{align} \left\{ \begin{aligned} &(1-\omega_l E)^n &+&\, (1-\omega_l^2 E)^n & + \cdots & + (1-\omega_l^l E)^n& =0 \\ &\omega_l^{-1}(1-\omega_l E)^n &+& \omega_l^{-2}(1-\omega_l^2 E)^n & +\cdots & +\omega_l^{-l}(1-\omega_l^l E)^n & =0 \\ & \cdots \\\, &\omega_l^{-(p-1)}(1-\omega_l E)^n &+&\, \omega_l^{-2(p-1)}(1-\omega_l^2 E)^n& +\cdots & +\omega_l^{-l(p-1)}(1-\omega_l^l E)^n & =0\\ &\omega_l^{-(p+1)}(1-\omega_l E)^n &+&\, \omega_l^{-2(p+1)}(1-\omega_l^2 E)^n & +\cdots & + \omega_l^{-l(p+1)}(1-\omega_l^l E)^n& =0\\ & \cdots \\ &\omega_l^{-(l-1)}(1-\omega_l E)^n &+&\, \omega_l^{-2(l-1)}(1-\omega_l^2 E)^n & +\cdots & +\omega_l^{-l(l-1)}(1-\omega_l^l E)^n & =0. \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} &(1-\omega_l E)^n &+&\, (1-\omega_l^2 E)^n & + \cdots & + (1-\omega_l^l E)^n& =0 \\ &\omega_l^{-1}(1-\omega_l E)^n &+& \omega_l^{-2}(1-\omega_l^2 E)^n & +\cdots & +\omega_l^{-l}(1-\omega_l^l E)^n & =0 \\ & \cdots \\\, &\omega_l^{-(p-1)}(1-\omega_l E)^n &+&\, \omega_l^{-2(p-1)}(1-\omega_l^2 E)^n& +\cdots & +\omega_l^{-l(p-1)}(1-\omega_l^l E)^n & =0\\ &\omega_l^{-(p+1)}(1-\omega_l E)^n &+&\, \omega_l^{-2(p+1)}(1-\omega_l^2 E)^n & +\cdots & + \omega_l^{-l(p+1)}(1-\omega_l^l E)^n& =0\\ & \cdots \\ &\omega_l^{-(l-1)}(1-\omega_l E)^n &+&\, \omega_l^{-2(l-1)}(1-\omega_l^2 E)^n & +\cdots & +\omega_l^{-l(l-1)}(1-\omega_l^l E)^n & =0. \end{aligned} \right. \end{align} $$
Let
![]() $\boldsymbol {\alpha }=((1-\omega _l E)^n, (1-\omega _l^2 E)^n, \ldots , (1-\omega _l^l E)^n)^T\in \mathbb {C}^{l}$
and
$\boldsymbol {\alpha }=((1-\omega _l E)^n, (1-\omega _l^2 E)^n, \ldots , (1-\omega _l^l E)^n)^T\in \mathbb {C}^{l}$
and
 $$ \begin{align*}A= \left(\begin{matrix}1&1&\cdots&1\\ \omega_l^{-1}&\omega_l^{-2}&\cdots& \omega_l^{-l}\\\vdots&\vdots&\cdots&\vdots\\ \omega_l^{-(p-1)}&\omega_l^{-2(p-1)}&\cdots& \omega_l^{-l(p-1)}\\ \omega_l^{-(p+1)}&\omega_l^{-2(p+1)}&\cdots& \omega_l^{-l(p+1)}\\ \vdots&\vdots&\cdots&\vdots\\ \omega_l^{-(l-1)}&\omega_l^{-2(l-1)}&\cdots&\omega_l^{-l(l-1)} \end{matrix}\right). \end{align*} $$
$$ \begin{align*}A= \left(\begin{matrix}1&1&\cdots&1\\ \omega_l^{-1}&\omega_l^{-2}&\cdots& \omega_l^{-l}\\\vdots&\vdots&\cdots&\vdots\\ \omega_l^{-(p-1)}&\omega_l^{-2(p-1)}&\cdots& \omega_l^{-l(p-1)}\\ \omega_l^{-(p+1)}&\omega_l^{-2(p+1)}&\cdots& \omega_l^{-l(p+1)}\\ \vdots&\vdots&\cdots&\vdots\\ \omega_l^{-(l-1)}&\omega_l^{-2(l-1)}&\cdots&\omega_l^{-l(l-1)} \end{matrix}\right). \end{align*} $$
Then we can also write (3.3) as
Since the rank
![]() $r(A)$
of the matrix A is exactly
$r(A)$
of the matrix A is exactly
![]() $l-1$
, the dimension of the linear space
$l-1$
, the dimension of the linear space
is exactly 1.
Let
![]() $\boldsymbol {\beta }=(\omega _{l}^{-(l-p)}, \ldots , \omega _{l}^{-p(l-p)}, \ldots , \omega _{l}^{-l(l-p)} )^{T}\in \mathbb {C}^{l}$
. Observe that
$\boldsymbol {\beta }=(\omega _{l}^{-(l-p)}, \ldots , \omega _{l}^{-p(l-p)}, \ldots , \omega _{l}^{-l(l-p)} )^{T}\in \mathbb {C}^{l}$
. Observe that
 $$ \begin{align*} &\omega_{l}^{-k}\cdot\omega_{l}^{-(l-p)}+ \omega_{l}^{-2k}\cdot\omega_{l}^{-2(l-p)}+\cdots+\omega_{l}^{-lk}\cdot\omega_{l}^{-l(l-p)}\\ &\quad =\frac{\omega_{l}^{-l(k+l-p)} \cdot\omega_{l}^{-(k+l-p)}-\omega_{l}^{-(k+l-p)} }{1-\omega_{l}^{-(k+l-p)} } =\frac{\omega_{l}^{-(k+l-p)}-\omega_{l}^{-(k+l-p)} }{1-\omega_{l}^{-(k+l-p)} }=0, \end{align*} $$
$$ \begin{align*} &\omega_{l}^{-k}\cdot\omega_{l}^{-(l-p)}+ \omega_{l}^{-2k}\cdot\omega_{l}^{-2(l-p)}+\cdots+\omega_{l}^{-lk}\cdot\omega_{l}^{-l(l-p)}\\ &\quad =\frac{\omega_{l}^{-l(k+l-p)} \cdot\omega_{l}^{-(k+l-p)}-\omega_{l}^{-(k+l-p)} }{1-\omega_{l}^{-(k+l-p)} } =\frac{\omega_{l}^{-(k+l-p)}-\omega_{l}^{-(k+l-p)} }{1-\omega_{l}^{-(k+l-p)} }=0, \end{align*} $$
where
![]() $k=0, 1, \ldots , p-1,p+1,\ldots ,l-1$
. It follows that
$k=0, 1, \ldots , p-1,p+1,\ldots ,l-1$
. It follows that
and
Therefore, there is a nonzero constant
![]() $k_0$
such that
$k_0$
such that
![]() $\alpha =k_0\beta $
, which yields
$\alpha =k_0\beta $
, which yields
Set
![]() $E=\rho e^{i \theta }$
. Then
$E=\rho e^{i \theta }$
. Then
does not depend on
![]() $k\,(1\leq k\leq l)$
. Equivalently,
$k\,(1\leq k\leq l)$
. Equivalently,
![]() $|\cos (\theta +{2k\pi }/{l})|$
is independent of k. However,
$|\cos (\theta +{2k\pi }/{l})|$
is independent of k. However,
leads to
![]() $l=1$
or
$l=1$
or
![]() $l=2$
. This contradicts our assumption that
$l=2$
. This contradicts our assumption that
![]() $l\geq 3$
. Therefore, we obtain
$l\geq 3$
. Therefore, we obtain
![]() $l=1$
or
$l=1$
or
![]() $l=2$
.
$l=2$
.
Step 3. Now, it suffices to consider the following two cases.
Case 1:
![]() $l=1$
, that is, there is a constant
$l=1$
, that is, there is a constant
![]() $C_1$
such that
$C_1$
such that
![]() $g(z+1)-g(z)=C_1$
. By the assumption in Theorem 1.5, it is easy to see that
$g(z+1)-g(z)=C_1$
. By the assumption in Theorem 1.5, it is easy to see that
![]() $C_1\notin \{2k\pi i: k\in \mathbb {Z}\}$
.
$C_1\notin \{2k\pi i: k\in \mathbb {Z}\}$
.
Case 2:
![]() $l=2$
, that is, there is a constant
$l=2$
, that is, there is a constant
![]() $C_2$
such that
$C_2$
such that
![]() $g(z+2)-g(z)=2C_2$
. It follows from (3.1) and (3.4) that
$g(z+2)-g(z)=2C_2$
. It follows from (3.1) and (3.4) that
where
 $$ \begin{align*} \phi_0=\frac{(1-e^{C_2})^n+(1+e^{C_2})^n}{2} \quad \mbox{and} \quad \phi_1=\frac{(1-e^{C_2})^n-(1+e^{C_2})^n}{2 e^{C_2}}. \end{align*} $$
$$ \begin{align*} \phi_0=\frac{(1-e^{C_2})^n+(1+e^{C_2})^n}{2} \quad \mbox{and} \quad \phi_1=\frac{(1-e^{C_2})^n-(1+e^{C_2})^n}{2 e^{C_2}}. \end{align*} $$
If
![]() $\phi _0\phi _1\neq 0$
, then applying Lemma 2.3 to (3.8) yields
$\phi _0\phi _1\neq 0$
, then applying Lemma 2.3 to (3.8) yields
which are both impossible. Thus,
![]() $\phi _0 \phi _1\equiv 0$
, which yields
$\phi _0 \phi _1\equiv 0$
, which yields
 $$ \begin{align*} \bigg(\frac{1+\exp C_2}{1-\exp C_2}\bigg)^{2n}=1. \end{align*} $$
$$ \begin{align*} \bigg(\frac{1+\exp C_2}{1-\exp C_2}\bigg)^{2n}=1. \end{align*} $$
This completes the proof of Theorem 1.5.
4 Proof of Theorem 1.6
Proof. As in the proof of Theorem 1.5, we can assume without loss of generality that
![]() $c=1$
. Since f is a transcendental entire function with hyper-order less than 1,
$c=1$
. Since f is a transcendental entire function with hyper-order less than 1,
 $$ \begin{align*} \limsup_{r\to +\infty}\frac{\log \log T(r,f)}{\log r}<1, \end{align*} $$
$$ \begin{align*} \limsup_{r\to +\infty}\frac{\log \log T(r,f)}{\log r}<1, \end{align*} $$
which yields
Together with the fact that
![]() $T(r, f)\leq \log M(r, f)\leq 3T(2r, f)$
, this gives
$T(r, f)\leq \log M(r, f)\leq 3T(2r, f)$
, this gives
It follows from Theorem 1.5 that
where
![]() $g(z)=h(z)+C_1 z$
,
$g(z)=h(z)+C_1 z$
,
![]() $h(z)$
is an entire function with period 1 or 2 and
$h(z)$
is an entire function with period 1 or 2 and
![]() $C_1$
is a constant. Then by Lemma 2.1,
$C_1$
is a constant. Then by Lemma 2.1,
for some absolute constant
![]() $C>0$
. This together with (4.1) yields
$C>0$
. This together with (4.1) yields
Thus,
If g is a polynomial, then the degree of g is exactly
![]() $1$
, in view of the fact that the hyper-order of f is less than 1. Thus,
$1$
, in view of the fact that the hyper-order of f is less than 1. Thus,
![]() $f(z)= e^{a z +b}$
, where
$f(z)= e^{a z +b}$
, where
![]() $a\neq 0$
and b are constants.
$a\neq 0$
and b are constants.
If g is a transcendental entire function, then according to (4.2),
![]() $H(z)=g'(z)$
is a periodic function with period 1 or 2. It is easy to see that for
$H(z)=g'(z)$
is a periodic function with period 1 or 2. It is easy to see that for
![]() $\alpha \in \mathbb {C}$
, if
$\alpha \in \mathbb {C}$
, if
![]() $\alpha $
is not a Picard exceptional value of H, then
$\alpha $
is not a Picard exceptional value of H, then
for some constant
![]() $C'>0$
. It follows that
$C'>0$
. It follows that
Thus,
which leads to a contradiction. Therefore, the theorem is proved.
Acknowledgements
The authors would like to thank the referee for valuable suggestions and comments. The authors also thank Yang Chengwei for help during the preparation of this paper.