Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T16:12:24.719Z Has data issue: false hasContentIssue false
  • English
  • Français

DIRECTIONAL TIME–FREQUENCY ANALYSIS VIA CONTINUOUS FRAMES

Part of: Numerical approximation and computational geometry Nontrigonometric harmonic analysis

Published online by Cambridge University Press:  30 April 2015

OLE CHRISTENSEN ,
BRIGITTE FORSTER  and
PETER MASSOPUST
OLE CHRISTENSEN
Affiliation:
Department of Applied Mathematics and Computer Science, Technical University of Denmark, Building 303, 2800 Lyngby, Denmark email ochr@dtu.dk
BRIGITTE FORSTER
Affiliation:
Fakultät für Informatik und Mathematik, Universität Passau, Innstr. 33, 94032 Passau, Germany email brigitte.forster@uni-passau.de
PETER MASSOPUST*
Affiliation:
Zentrum Mathematik, Lehrstuhl M6, Technische Universität München, Boltzmannstr. 3, 85747 Garching, Germany Helmholtz Zentrum München, Ingolstädter Landstr. 1, 85764 Neuherberg, Germany email massopust@ma.tum.de
*
✉massopust@ma.tum.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Grafakos and Sansing [‘Gabor frames and directional time–frequency analysis’, Appl. Comput. Harmon. Anal.25 (2008), 47–67] have shown how to obtain directionally sensitive time–frequency decompositions in 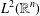$L^{2}(\mathbb{R}^{n})$ based on Gabor systems in 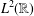$L^{2}(\mathbb{R})$. The key tool is the ‘ridge idea’, which lifts a function of one variable to a function of several variables. We generalise their result in two steps: first by showing that similar results hold starting with general frames for 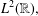$L^{2}(\mathbb{R}),$ in the settings of both discrete frames and continuous frames, and second by extending the representations to Sobolev spaces. The first step allows us to apply the theory to several other classes of frames, for example wavelet frames and shift-invariant systems, and the second one significantly extends the class of examples and applications. We consider applications to the Meyer wavelet and complex B-splines. In the special case of wavelet systems we show how to discretise the representations using ${\it\epsilon}$-nets.

Keywords

discrete and continuous framesridge functiondirectionally sensitive time–frequency decompositioncomplex B-splinediscretisation of the sphere

MSC classification

Primary: 42C15: General harmonic expansions, frames
Secondary: 42C40: Wavelets and other special systems 65D07: Splines
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 92 , Issue 2 , October 2015 , pp. 268 - 281
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Ali, S., Antoine, J.-P. and Gazeau, J.-P., ‘Continuous frames in Hilbert space’, Ann. Phys. 222(1) (1993), 1–37.CrossRefGoogle Scholar
Aubin, J. P., Applied Functional Analysis (John Wiley, New York, 2000).CrossRefGoogle Scholar
Brauchart, J. S. and Hesse, K., ‘Numerical integration over spheres of arbitrary dimension’, Constr. Approx. 25 (2007), 41–71.CrossRefGoogle Scholar
Candès, E., ‘Harmonic analysis of neural network’, Appl. Comput. Harmon. Anal. 6 (1999), 197–218.CrossRefGoogle Scholar
Candès, E. and Donoho, D., ‘Ridgelets: the key to higher-dimensional intermittency?’, Philos. Trans. R. Soc. Lond. Ser. A 357 (1999), 2495–2509.CrossRefGoogle Scholar
Candès, E. and Donoho, D., ‘New tight frames of curvelets and optimal representation of objects with piecewise C 2 -singularities’, Comm. Pure Appl. Math. 57 (2004), 219–266.CrossRefGoogle Scholar
Christensen, O., Frames and Bases. An Introductory Course (Birkhäuser, Boston, MA, 2007).Google Scholar
Christensen, O. and Kim, R. Y., ‘On dual Gabor frame pairs generated by polynomials’, J. Fourier Anal. Appl. 16 (2010), 1–16.CrossRefGoogle Scholar
Christensen, O. and Massopust, P., ‘Exponential B-splines and the partition of unity property’, Adv. Comput. Math. 37(3) (2012), 301–318.CrossRefGoogle Scholar
Chui, C., He, W. and Stöckler, J., ‘Compactly supported tight and sibling frames with maximum vanishing moments’, Appl. Comput. Harmon. Anal. 13(3) (2002), 226–262.CrossRefGoogle Scholar
Conrad, M. and Prestin, J., ‘Multiresolution on the sphere’, in: Tutorials on Multiresolution in Geometric Modelling, Mathematics and Visualization (eds. Iske, A., Quak, E. and Floater, M. S.) (Springer, Berlin–Heidelberg, 2002), 165–202.CrossRefGoogle Scholar
Daubechies, I., Ten Lectures on Wavelets (SIAM, Philadelphia, PA, 1992).CrossRefGoogle Scholar
Daubechies, I., Han, B., Ron, A. and Shen, Z., ‘Framelets: MRA-based constructions of wavelet frames’, Appl. Comput. Harmon. Anal. 14(1) (2003), 1–46.CrossRefGoogle Scholar
Forster, B., ‘Five good reasons for complex-valued transforms in image processing’, in: New Perspectives on Approximation and Sampling Theory (eds. Zayed, A. and Schmeisser, G.) (Birkhäuser, Basel, 2014).Google Scholar
Forster, B., Blu, T. and Unser, M., ‘Complex B-splines’, Appl. Comput. Harmon. Anal. 20 (2006), 281–282.CrossRefGoogle Scholar
Go, K. and Labate, D., ‘S-optimally sparse multidimensional representations using shearlets’, SIAM J. Math. Anal. 39(1) (2007), 298–318.CrossRefGoogle Scholar
Grafakos, L. and Sansing, C., ‘Gabor frames and directional time–frequency analysis’, Appl. Comput. Harmon. Anal. 25 (2008), 47–67.CrossRefGoogle Scholar
Gröchenig, K., Foundations of Time–Frequency Analysis (Birkhäuser, Boston, MA, 2001).CrossRefGoogle Scholar
Haroske, D. D. and Triebel, H., Distributions, Sobolev spaces, Elliptic Equations (European Mathematical Society, Zurich, 2008).Google Scholar
Hur, Y. and Ron, A., ‘L-CAMP: extremely local high-performance wavelet representations in high spatial dimension’, IEEE Trans. Inform. Theory 54 (2008), 2196–2208.CrossRefGoogle Scholar
Kaiser, G., A Friendly Guide to Wavelets (Birkhäuser, Boston, MA, 1994).Google Scholar
Kim, I., ‘Gabor frames with trigonometric spline dual windows’, Asian-Eur. J. Math., to appear.Google Scholar
Labate, D., Lim, W.-Q, Kutyniok, G. and Weiss, G., ‘Sparse multidimensional representation using shearlets’, in: Wavelets XI (San Diego, CA, 2005), SPIE Proceedings, 5914 (SPIE, Bellingham, WA, 2005), 254–262.Google Scholar
Laugesen, R. S., ‘Gabor dual spline windows’, Appl. Comput. Harmon. Anal. 27 (2009), 180–194.CrossRefGoogle Scholar
Louis, A. K., Maaß, P. and Rieder, A., Wavelets: Theorie und Anwendung, 1st edn (Teubner, Stuttgart, 1994).CrossRefGoogle Scholar
Narcowich, F. J. and Ward, J. D., ‘Nonstationary wavelets on the m-sphere for scattered data’, Appl. Comput. Harmon. Anal. 3(4) (1996), 324–336.CrossRefGoogle Scholar
Natterer, F., The Mathematics of Computerized Tomography (SIAM, Philadelphia, PA, 2001).CrossRefGoogle Scholar
Pinkus, A., ‘Interpolation by ridge functions’, J. Approx. Theory 73 (1993), 218–236.Google Scholar
Ron, A. and Shen, Z., ‘Affine systems in L 2(ℝd) II: dual systems’, J. Fourier Anal. Appl. 3 (1997), 617–637.CrossRefGoogle Scholar
Rudin, W., Functional Analysis, 2nd edn (McGraw-Hill, New York, 1991).Google Scholar
Sutherland, W. A., Introduction to Metric and Topological Spaces (Oxford University Press, Oxford, 1975).Google Scholar
Triebel, H., Theory of Function Spaces (Birkhäuser, Basel, 2010).Google Scholar
Wojtaszczyk, P., A Mathematical Introduction to Wavelets (Cambridge University Press, Cambridge, 1999).Google Scholar