Published online by Cambridge University Press: 13 September 2019
For every integer 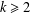 $k\geq 2$ and every
$k\geq 2$ and every 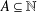 $A\subseteq \mathbb{N}$, we define the
$A\subseteq \mathbb{N}$, we define the 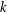 $k$-directions sets of
$k$-directions sets of 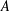 $A$ as
$A$ as 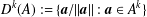 $D^{k}(A):=\{\boldsymbol{a}/\Vert \boldsymbol{a}\Vert :\boldsymbol{a}\in A^{k}\}$ and
$D^{k}(A):=\{\boldsymbol{a}/\Vert \boldsymbol{a}\Vert :\boldsymbol{a}\in A^{k}\}$ and 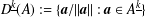 $D^{\text{}\underline{k}}(A):=\{\boldsymbol{a}/\Vert \boldsymbol{a}\Vert :\boldsymbol{a}\in A^{\text{}\underline{k}}\}$, where
$D^{\text{}\underline{k}}(A):=\{\boldsymbol{a}/\Vert \boldsymbol{a}\Vert :\boldsymbol{a}\in A^{\text{}\underline{k}}\}$, where  $\Vert \cdot \Vert$ is the Euclidean norm and
$\Vert \cdot \Vert$ is the Euclidean norm and 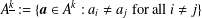 $A^{\text{}\underline{k}}:=\{\boldsymbol{a}\in A^{k}:a_{i}\neq a_{j}\text{ for all }i\neq j\}$. Via an appropriate homeomorphism,
$A^{\text{}\underline{k}}:=\{\boldsymbol{a}\in A^{k}:a_{i}\neq a_{j}\text{ for all }i\neq j\}$. Via an appropriate homeomorphism,  $D^{k}(A)$ is a generalisation of the ratio set
$D^{k}(A)$ is a generalisation of the ratio set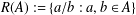 $R(A):=\{a/b:a,b\in A\}$. We study
$R(A):=\{a/b:a,b\in A\}$. We study 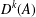 $D^{k}(A)$ and
$D^{k}(A)$ and 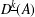 $D^{\text{}\underline{k}}(A)$ as subspaces of
$D^{\text{}\underline{k}}(A)$ as subspaces of 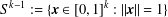 $S^{k-1}:=\{\boldsymbol{x}\in [0,1]^{k}:\Vert \boldsymbol{x}\Vert =1\}$. In particular, generalising a result of Bukor and Tóth, we provide a characterisation of the sets
$S^{k-1}:=\{\boldsymbol{x}\in [0,1]^{k}:\Vert \boldsymbol{x}\Vert =1\}$. In particular, generalising a result of Bukor and Tóth, we provide a characterisation of the sets 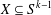 $X\subseteq S^{k-1}$ such that there exists
$X\subseteq S^{k-1}$ such that there exists 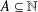 $A\subseteq \mathbb{N}$ satisfying
$A\subseteq \mathbb{N}$ satisfying 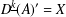 $D^{\text{}\underline{k}}(A)^{\prime }=X$, where
$D^{\text{}\underline{k}}(A)^{\prime }=X$, where 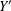 $Y^{\prime }$ denotes the set of accumulation points of
$Y^{\prime }$ denotes the set of accumulation points of 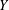 $Y$. Moreover, we provide a simple sufficient condition for
$Y$. Moreover, we provide a simple sufficient condition for 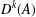 $D^{k}(A)$ to be dense in
$D^{k}(A)$ to be dense in 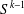 $S^{k-1}$. We conclude with questions for further research.
$S^{k-1}$. We conclude with questions for further research.
P. Leonetti is supported by the Austrian Science Fund (FWF), project F5512-N26; C. Sanna is supported by a postdoctoral fellowship of INdAM and is a member of the INdAM group GNSAGA.