No CrossRef data available.
Article contents
DISCREPANCY BOUNDS FOR THE DISTRIBUTION OF RANKIN–SELBERG L-FUNCTIONS
Published online by Cambridge University Press: 18 October 2024
Abstract
We investigate the discrepancy between the distributions of the random variable 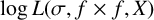 $\log L (\sigma , f \times f, X)$ and that of
$\log L (\sigma , f \times f, X)$ and that of 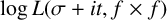 $\log L(\sigma +it, f \times f)$, that is,
$\log L(\sigma +it, f \times f)$, that is, 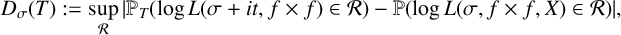 $$ \begin{align*} D_{\sigma} (T) := \sup_{\mathcal{R}} |\mathbb{P}_T(\log L(\sigma+it, f \times f) \in \mathcal{R}) - \mathbb{P}(\log L(\sigma, f \times f, X) \in \mathcal{R})|, \end{align*} $$
$$ \begin{align*} D_{\sigma} (T) := \sup_{\mathcal{R}} |\mathbb{P}_T(\log L(\sigma+it, f \times f) \in \mathcal{R}) - \mathbb{P}(\log L(\sigma, f \times f, X) \in \mathcal{R})|, \end{align*} $$
where the supremum is taken over rectangles 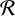 $\mathcal {R}$ with sides parallel to the coordinate axes. For fixed
$\mathcal {R}$ with sides parallel to the coordinate axes. For fixed 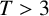 $T>3$ and
$T>3$ and 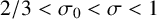 $2/3 <\sigma _0 < \sigma < 1$, we prove that
$2/3 <\sigma _0 < \sigma < 1$, we prove that 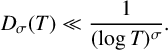 $$ \begin{align*} D_{\sigma} (T) \ll \frac{1}{(\log T)^{\sigma}}. \end{align*} $$
$$ \begin{align*} D_{\sigma} (T) \ll \frac{1}{(\log T)^{\sigma}}. \end{align*} $$
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 111 , Issue 1 , February 2025 , pp. 32 - 42
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The author is supported by The Science and Technology Development Fund, Macau SAR (File no. 0084/2022/A).


